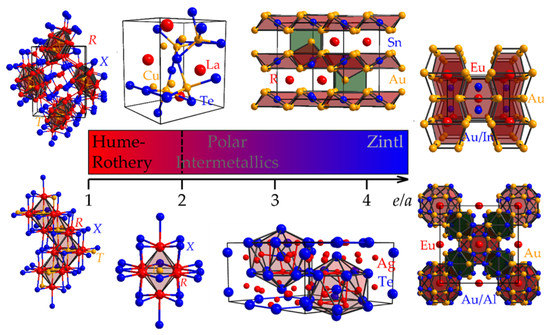
Revealing Tendencies in the Electronic Structures of Polar Intermetallic Compounds

Abstract

The quest for solid-state materials with tailored chemical and physical features stimulates the search for general prescriptions to recognize and forecast their electronic structures providing valuable information about the experimentally determined bulk properties at the atomic scale. Although the concepts first introduced by Zintl and Hume–Rothery help to understand and forecast the bonding motifs in several intermetallic compounds, there is an emerging group of compounds dubbed as polar intermetallic phases whose electronic structures cannot be categorized by the aforementioned conceptions. These polar intermetallic compounds can be divided into two categories based on the building units in their crystal structures and the expected charge distributions between their components. On the one hand, there are polar intermetallic compounds composed of polycationic clusters surrounded by anionic ligands, while, on the other hand, the crystal structures of other polar intermetallic compounds comprise polyanionic units combined with monoatomic cations. In this review, we present the quantum chemical techniques to gain access to the electronic structures of polar intermetallic compounds, evaluate certain trends from a survey of the electronic structures of diverse polar intermetallic compounds, and show options based on quantum chemical approaches to predict the properties of such materials.

1. Introduction

For a given material, the knowledge of its electronic structure that is distributed through chemical bonds between atoms arranged in a well-defined long-range order in its crystal structure provides valuable information about the physical properties of the respective compound [1]. Because the comprehension of materials properties is worthwhile to tailor compounds with projected features, there is a great desire among materials scientists to establish fundamental directives which allow distinguishing and predicting the relations between the crystal structures, electronic structures and physical properties in solid state materials [1]. An important role in the findings of the aforementioned directives plays the identifications of bonding motifs in compounds for the reason that the recognition of the nature of bonding and its energetic contributions (beside those of the site energy) for a given material facilitates to understand the local structural arrangements and, based on these, the compositions of materials as well as the circulations of electrons through them [1].

For the cases of molecules consisting of non-metal elements of the periodic table, straightforward prescriptions such as the octet rule [2] or the concept of hypervalency [3,4] help to recognize and, furthermore, forecast the nature of bonding in them. To identify the bonding patterns (and stability trends) for several intermetallic compounds comprising structural fragments in the forms of homo- or heteroatomic chains or clusters, certain plans, e.g., the Zintl–Klemm or the Hume–Rothery concept, have been developed (references of certain reviews about the two aforementioned concepts have been provided in

Table 1. Overview about selected reviews regarding compounds to which the Zintl–Klemm or the Hume–Rothery concept can be applied.

Year Published	Authors	Contents	Ref.
1937	H. Jones	Quantitative development of a model to account for the Hume–Rothery (H.-R.) concept	[8]
1939	E. Zintl	Overview about polyanions dissolved in liquid ammonia	[9]
1963	W. Klemm, E. Busmann	Application of the pseudoatom approach	[10]
1973	H. Schäfer, B. Eisenmann et al.	Survey of alkali and alkaline-earth metal triels, tetrels, pnictogens and chalcogenides and definition of the Zintl concept	[11]
1978	T. B. Massalski, U. Mizutani	Summary of the main features of the electronic structures in H.-R. phases with special emphasis on their impacts on the stability of a given H.-R. phase	[12]
1997	J. Beck	Applications of the Zintl concept to chalcogen polycations	[13]
2000	G. A. Papoian, R. Hoffmann	Extension of the Zintl–Klemm concept based on the supposition of hypervalent bonding in electron-rich networks	[14]
2006	S. C. Sevov, J. M. Goicoechea	Evaluation of the reactivity of nine-atom deltahedral clusters with emphasis on their redox chemistry, cluster geometries and nature of bonding	[15]
2007	Kauzlarich, S. M. Brown S. R. et al.	Overview about applications of Zintl phases as materials for thermoelectric energy conversion	[16]
2008	J. Köhler, M.-W. Whangbo	Overview about late transition metals acting as Zintl anions	[17]
2010	S. Scharfe, T. Fässler	Summary of reactions of nine-atom polyhedral clusters	[18]
2010	E. S. Toberer, A. F. May et al.	Survey of Zintl phases suited as materials for thermoelectric energy conversion	[19]
2011	J.-M. Dubois, E. Belin-Ferré et al.	Review about the applicability of the H.-R. concept to complex metallic alloys	[20]
2011	S. Scharfe, F. Kraus et al.	Overview about the syntheses, properties, structural arrangements and electronic structures of dissolved Zintl ions of groups 14 and 15 elements	[21]
2011	G. J. Miller, M. W. Schmidt et al.	Survey of quantum chemical investigations to probe the validity of the Zintl–Klemm concept	[22]
2014	R. Nesper	Historical survey of the developments of the Zintl–Klemm concept	[23]
2017	U. Mizutani, H. Sato	Review about the origin of pseudogaps at the Fermi levels and the electron concentration rule for Hume–Rothery phases	[24]

). Under consideration of the Zintl–Klemm concept, the electrons are transferred from the more electropositive to the more electronegative elements that form anions being isostructural to modifications of isoelectronic elements, while certain types of structures identified for the binary Cu–Zn system can be assigned to specific valence electron concentrations based on the Hume–Rothery rules. Although the two aforesaid concepts help to understand the bonding motifs in quite a lot of intermetallic compounds, there is an emerging group of intermetallic compounds classified as polar intermetallic phases which comprise polar intermetallic bonds but lack in straightforward valence electron rules [5,6,7]. These polar intermetallic phases show lower valence electron concentration (e/a) relative to those of the Zintl phases, but close to those of the Hume–Rothery phases (Scheme 1). The existence of such polar intermetallic phases raises the question of whether there are previously unknown fundamental directives that help to classify and to forecast the nature of bonding in them.

In this review, a series of electronic structures and bonding motifs will be evaluated for the examples of certain polar intermetallic compounds to examine the feasibility of general prescriptions which are suited to describe the bonding motifs for such materials. In this connection, we will focus on the electronic structures and the bonding motifs of intermetallic compounds comprising polycationic agglomerates paired with anionic ligands as well as polyanionic fragments combined with monoatomic cations [5]. In addition, an overview of current quantum chemical approaches to predict the existence and the properties of intermetallic compounds will be provided.

2. Quantum Chemical Methodologies Employed to Reveal the Nature of Bonding in Intermetallic Compounds

To obtain the energy of a many-particle system, that is, the sum of the potential and the kinetic energy of the given system, solving at least the time-independent Schrödinger equation is needed [26]

Hψ = Eψ

with H as the Hamilton operator

$$H=-{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}\frac{{ħ}^2}{2\mathrm{m}}{\nabla }_{\mathrm{i}}^2-{\displaystyle \sum }_{\mathrm{A}=1}^{\mathrm{M}}\frac{{ħ}^2}{{2\mathrm{M}}_{\mathrm{A}}}{\nabla }_{\mathrm{A}}^2-\frac{1}{{4\mathsf{\pi }\mathsf{\epsilon }}_0}\left({\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\displaystyle \sum }_{\mathrm{A}=1}^{\mathrm{M}}\frac{{\mathrm{e}}^2{\mathrm{Z}}_{\mathrm{A}}}{{\mathrm{r}}_{\mathrm{iA}}}-{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\displaystyle \sum }_{\mathrm{j}>\mathrm{i}}^{\mathrm{N}}\frac{{\mathrm{e}}^2}{{\mathrm{r}}_{\mathrm{ij}}}-{\displaystyle \sum }_{\mathrm{A}=1}^{\mathrm{M}}{\displaystyle \sum }_{\mathrm{B}>\mathrm{A}}^{\mathrm{M}}\frac{{\mathrm{e}}^2{\mathrm{Z}}_{\mathrm{A}}{\mathrm{Z}}_{\mathrm{B}}}{{\mathrm{R}}_{\mathrm{AB}}}\right)$$

for a system of electrons and nuclei. While a linear combination of atomic orbitals may be employed to solve Schrödinger’s equation for molecules, in the cases of extended solid-state materials, Bloch’s theorem [27] is used to construct wave functions fulfilling Schrödinger’s equation. The prerequisite of translation symmetry in order to construct wave functions following Bloch’s theorem also means that the crystal structure of a given solid-state material needs to be well ordered to generate starting positional parameters suited for quantum chemical examinations; however, the crystal structures of several intermetallic compounds exhibit atomic sites with positional or occupational disorders (see below), which cannot be used as starting parameters for the electronic structure calculations. For the cases of intermetallic compounds with disordered atomic sites in their crystal structures, the electronic structure calculations are typically performed for models which approximate the actual crystal, are structurally optimized prior to the electronic structure computations and correspond to the lowest total energies (for details regarding the generations of such models, we refer to the literature provided in Table 4).

Because an exact determination of the energy of a many-particle system in a solid-state material lies behind the scope of today’s computational resources, the energy of many-particle systems in extended solids needs to be approached by approximations [28]. Due to the continuous developments in the quantum chemical methodologies and the available computational capacities, there are diverse quantum chemical methods which have been employed to reveal the electronic band structures and the nature of bonding in intermetallic compounds. In the following, a brief survey of the concepts behind some approaches will be presented (detailed overviews about the methodological approaches and diverse programs may be extracted elsewhere, see, e.g., [28]).

The semiempirical extended Hückel method that is principally equivalent to the empirical tight-binding method was one of the very first approaches to compute the electronic structures in solid-state materials [29]. In this approach, the valence orbitals are exclusively taken into consideration and certain entries, particularly, for the interaction (H_μν) and the overlap (S_μν) integrals, of the secular determinant, which needs to be solved to obtain the lowest energy for a linear combination of atomic orbitals (LCAO), are parameterized. In particular, the overlap matrix elements (S_μν) are computed using Slater-type orbitals, while the interaction matrix elements (H_μν) are evaluated solving the Wolfsberg–Helmholz formula [30] based on the Coulomb matrix elements (H_μμ) which are derived from the experimentally determined ionization potentials. To extract information about the chemical bonding from extended Hückel theory-based electronic band structure calculations on solid-state materials, the crystal orbital overlap population (COOP) method, in which the densities-of-states are weighted by the respective overlap populations, has been introduced [31]. In the COOP approach, bonding and antibonding interactions between pairs of atoms are indicated by positive and negative values of the COOP curves, respectively.

One approach to overcome issues arising from the descriptions of correlation and exchange between electrons is based on the uses of electron density functions as wave functions in the framework of the density-functional-theory [32,33,34]. To enhance the velocity of the computations, plane waves (and related functions), which can be derived from Bloch’s theorem, are typically employed as basis sets of density-functional-theory-based computations [28]. In the case of the augmented-plane wave method, the plane wave functions are constructed based on atomic functions within muffin-tin spheres which define the boundaries of muffin-tin-like potentials, and a plane wave outside that sphere [35]. Because the energy-dependence of such augmented-plane-wave functions drastically limits the speed of the computations, it is convenient to develop Taylor series of the energies for the radial parts of the inner functions and to truncate these series after the second term (linear methods) [36]. To date, different variants to compute the electronic band structures in solid state materials have been developed based on the previously described linearized augmented plane-wave (LAPW) approach. For instance, the full-potential linearized augmented plane-wave (FLAPW) procedure employs full instead of muffin-tin-type potentials, while the linearized muffin-tin orbital (LMTO) method utilizes Hankel instead of plane-wave functions [28]. The projector augmented-wave (PAW) approach [37] is a different and more recently developed (all-electron) method, in which pseudopotentials used to replace ion-electron potentials are adjusted in the calculations based on full wave functions.

An extraction of the information about the chemical bonding from LMTO- and PAW-based electronic structure computations on solids may be accomplished with the aid of the crystal orbital Hamilton population (COHP) method, in which the density-of-states matrix is weighted by the respective Hamilton matrix elements [38,39]. In contrast to the aforementioned COOP method (see above), bonding and antibonding interactions are represented by negative and positive values of the COHP. Notably, a direct comparison between the COHP values of compounds with dissimilar compositions cannot be accomplished, because the average electrostatic potential of each density-functional-theory-based computation is set to an arbitrary “zero” energy, whose relative position varies for systems with different compositions [28]. To provide insight into the differences between the sorts of bonding in compounds with dissimilar compositions, the cumulative integrated COHP values (ICOHP), which are obtained by weighting the ICOHP values of all nearest neighbor interactions by the respective bond frequencies, are typically projected as percentages of the net bonding capabilities (examples, to which that procedure was applied, are provided in

Table 2. Average −ICOHP/bond values and percentages of the respective interactions to the net bonding capabilities in rare-earth transition-metal halides comprising tetrameric clusters, [T₄R₁₆]. The details regarding the quantum chemical computations, distance ranges, −ICOHP/bond ranges and cumulative −ICOHP/cell values of all compounds listed in Table 2 have been reported elsewhere [59].

Compound	R–T		R–R		R–X		T–T
	Ave. −ICOHP/bond [ev/bond]	%	Ave. −ICOHP/bond [ev/bond]	%	Ave. −ICOHP/bond [ev/bond]	%	Ave. −ICOHP/bond [ev/bond]	%
[Ru4Y16]Br20	2.03	48.8	0.11	5.2	0.60	43.2	0.48	2.9
[Ru4Y16]I20	1.89	50.1	0.08	4.5	0.56	44.2	0.18	1.2
[Ir4Y16]Br24	2.03	41.9	0.08	3.5	0.80	51.8	0.60	2.8
[Ru4Ho16]I24(Ho4I4)	2.02	39.0	0.09	4.1	0.71	54.9	0.42	2.0
[Ir4Tb16]Cl24(TbCl3)4	2.12	35.3	0.10	3.4	0.87	57.2	0.86	3.6
[Rh4Tb16]Br24(TbBr3)4	2.17	34.0	0.14	4.5	0.95	59.6	0.49	1.9
[Ir4Tb16]Br24(TbBr3)4	2.41	37.4	0.11	3.7	0.90	56.0	0.77	3.0
[Ir4Sc16]Cl24(ScCl3)4	2.16	33.6	0.08	2.7	0.95	59.1	1.25	4.9
[Os4Sc16]Cl24(ScCl3)4	2.26	33.5	0.09	2.7	0.98	58.0	1.57	5.8
[Ru4Sc16]Cl24(ScCl3)4	2.08	31.6	0.10	3.3	1.01	61.1	1.07	4.0
[Ru4Gd16]Br24(GdBr3)4	2.47	35.5	0.16	4.8	1.00	57.6	0.62	2.2

and Table 4). Other approaches to analyze the electronic structures in solid state materials include the electron localization functions [40,41] (ELF) and the quantum theory of atoms in molecules [42] (QTAIM). In the ELF method, the localization of electrons (and, hence, chemical bonds) in a given material is related to the probability to encounter a pair of electrons with like spins, while the QTAIM procedure enables the assignments of effective charges to atoms within a given material.

3. Tendencies Within Bonding Motifs in Compounds with Polycationic Fragments Paired with Anionic Ligands

This group comprises compounds whose crystal structures are composed of transition-metal atom building units of polyhedral shape (“clusters”) enclosed by halide (X) or telluride ligands [5]. The clusters constituted by the electron-poorer early transition-metal atoms, i.e., groups 3 or 4 elements, typically enclose endohedral atoms [43,44,45] which can be main group or transition-metal (T) elements (lists of the diverse endohedral atoms observed to be incorporated in such transition-metal atom clusters have been reported elsewhere [43,46,47]). For the cases of the clusters enclosing endohedral late transition-metal atoms, strong (polar) intermetallic bonds are evident for the contacts between the host atoms and the early transition element atoms that surround them (see below) [45,46,47]. Previous examinations on the late transition-metal centered rare-earth metal (R) cluster halides revealed the occurrence of clusters which are condensed to cluster oligomers or cluster chains by sharing common vertices, edges or faces as well as isolated clusters that are surrounded solely by the halide ligands (Figure 1) [47,48]. Although one might expect such halides to be salt-like, the results of the measurements of the temperature-dependent transport properties for certain metal-rich (≥50 at.-% T/R) representatives of this group indicate metallic conductivity for them [49,50]. In the following, the bonding motifs in representatives crystallizing with the most prolific structure types presently identified for the ternary rare-earth transition-metal halides will be examined for the feasibility of the above proposed general directives.

The amounts of cluster-based electrons (CBEs) are usually obtained by subtracting the numbers of halide ligands from the net valence electron counts of the transition-metal centered rare-earth metal cluster [45]. For instance, applying this scheme to formally distribute electrons in the previously reported Y₇I₁₂Co yields a total of 18 CBEs (=7∙3 + 9 – 12), which is expected to correspond to (preferable) closed-shell configurations for the [TR₆]X₁₂R-type compounds [51,52,53]. Further research on the electronic structures of transition-metal centered rare-earth metal cluster halides crystallizing with the [TR₆]X₁₀-type whose crystal structure also comprises isolated octahedral [TR₆] clusters as observed for the [TR₆]X₁₂R-type (Figure 1) revealed that closed-shell configurations are also achieved for a total of 18 CBEs (an overview about the [TR₆]X₁₂R-type as well as [TR₆]X₁₀-type halides identified to date has been provided elsewhere [54]). The results of the density-functional-theory-based computations for a series of [TR₆]X₁₀-type compounds indicate that the total bond energy is optimized through full occupations of R–T bonding interactions for a cluster compound with a group 10 interstitial, for which a total of 18 CBEs is accomplished [54].

Among the class of ternary rare-earth transition-metal halides composed of transition-metal centered rare-earth cluster oligomers, one sort of tetramers (represented by the notation [T₄R₁₆]) has been encountered frequently and has been identified for the crystal structures of four different types of ternary rare-earth transition-metal halides with the net formulas [T₄R₁₆]X₂₈[R₄] [55], [T₄R₁₆]X₂₀ [56], [T₄R₁₆]X₂₄[RX₃]₄ [57] and [T₄R₁₆]X₂₄ [57]. The arrangements of these tetramers may be depicted as pairs of dimers, i.e., two one-edge-sharing transition-metal centered rare-earth metal octahedrons, which are arranged perpendicular to each other and condense via four common edges to assemble the tetramers enclosed by 36 halido ligands (Figure 1). Alternatively, the R₁₆ skeletons of these tetramers can be described as all vertices truncated supertetrahedrons or Friauf-polyhedrons. An overview about all ternary rare-earth transition-metal halides whose crystal structures have to date been determined to comprise the aforementioned tetramers has been reported elsewhere [58]. A survey of all hitherto discovered ternary rare-earth transition-metal halides comprising these [T₄R₁₆] tetramers implied that the maximum amounts of cluster-based electrons (CBEs) are accomplished for counts of 15 electrons per [TR₆] octahedron [58]. An examination of the first-principles-based electronic band structure calculations for a series of rare-earth transition-metal halides containing the tetramers revealed that the majority of the bonding populations resides between the heteroatomic R–X and R–T contacts, while homoatomic R–R and T–T bonding plays a subordinate role (Table 2) [59]. Further research on the energy regions near the Fermi levels in these halides revealed the presence of gaps corresponding to closed-shell-configurations for CBE counts of 15 electrons as electronically favorable situations whose accomplishments can be considered as the driving forces of the tendency to achieve totals of 15 CBEs per [TR₆] octahedron [59].

One prolific group of ternary rare-earth transition-metal halides containing cluster chains is the class of those halides with the net formula [TR₃]X₃, for which five different types of structure have been reported [60,61,62,63]. In particular, determinations of the crystal structures for the [TR₃]X₃-type halides of the early lanthanides (R = La–Pr) revealed that these halides may adopt four of the aforementioned different types of structure [49]. Further research on the [TR₃]X₃-type halides of the early lanthanides (R = La–Pr) bared that the monoclinic [RuPr₃]I₃-type has been observed solely for iodides and bromides with group eight elements as endohedral atoms within the lanthanide clusters, while another structurally independent type, that is, the cubic [PtPr₃]I₃-type, has been adopted by bromides and iodides comprising endohedral atoms of groups 8–11 [49]. In the cubic [PtPr₃]I₃-type, the [TR₆] octahedrons condense via three common edges to assemble helical cluster chains, whereas octahedral [TR₆] cluster share four common edges with other [TR₆] units to form bioctahedral chains in the monoclinic structure. The remaining edges of the [TR₆] clusters, which are not capped by the endohedral transition-metal atoms of the neighboring rare-earth metal clusters, are capped by the halide ligands in a μ₂-fashion (Figure 1). Because the [TR₃]X₃-type rare-earth transition-metal halides with group eight elements as endohedral atoms possess the same amounts of cluster-based electrons (CBEs), at this point, one may wonder which factors control the adaption of the respective type of structure. Examinations [64] of the electronic band structures and the nature of chemical bonding for isocompositional representatives of both [TR₃]X₃-types with group eight interstitials indicate that the Fermi level in the cubic structure falls in a maximum of the DOS, while the Fermi level in the monoclinic [TR₃]X₃-type representative is located in a narrow gap. The bonding in these rare-earth transition-metal halides is dominated by the heteroatomic R–T as well as R–X interactions beside minor, but evident R–R interactions (Figure 1). As the presence of a peak at the Fermi level typically points to an electronic instability, the monoclinic [TR₃]X₃-type should be preferred for the [TR₃]X₃-type halides containing group eight elements as interstitials of the rare-earth clusters; however, the chemical bonding analysis for both representatives showed that the monoclinic structure comprises less “polar” heteroatomic contributions, which, on the contrary, are maximized in the cubic form. Therefore, the structural preferences between the cubic and the monoclinic [TR₃]X₃-types are controlled by the interplay to achieve an electronically favorable situation and, on the other hand, to maximize overall bonding. Notably, further research demonstrated that the Fermi level falls in the pseudogap for cubic [TR₃]X₃-type halides containing group nine interstitials thereby achieving an electronically favorable situation.

The transition-metal-centered rare-earth cluster chains observed for certain rare-earth transition-metal halides have also been determined to exist in the crystal structures for certain rare-earth transition-metal tellurides (an overview of the hitherto determined rare-earth transition-metal tellurides comprising groups 7–11 elements is provided in

Table 3. Overview about the rare-earth transition-metal tellurides hitherto reported for the group seven to eleven elements.

). For instance, the chains of face-sharing transition-metal-centered scandium cubes (C) and square antiprisms (A) with the stacking sequences of –C–A–A–C–A–A– within the chains in [T₃Sc₁₄]Te₈ (T = Ru, Os; Figure 2b) show the same topologies as the iridium-centered scandium cluster chains in [Ir₃Sc₁₂]Br₁₆ (Figure 2a) [65,66]. Analyses of the nature of bonding in the telluride and the bromide indicated that the bonding in these materials is dominated by the heteroatomic interactions. Another example of the rare-earth transition-metal tellurides whose crystal structure comprises transition-metal centered rare-earth cluster chains with topologies similar to those observed for the transition-metal centered rare-earth cluster chains in certain rare-earth transition-metal halides is [NiGd₄]Te₂ [67]. In this rare-earth transition-metal telluride, the nickel atoms reside in monocapped gadolinium trigonal prisms [NiGd₇], which are condensed via two common rectangular faces to assemble double chains enclosed by the tellurium atoms (Figure 2d). The topologies of these transition-metal-centered rare-earth cluster double chains are similar to those found for the rare-earth cluster chains in [TR₃]X₃-type iodides with R = Y, Gd and T = Mn, Ru, Ir (not all combinations; Figure 2c) [55,62,67]. Analyses of the electronic structures for diverse representatives of the metal-rich rare-earth transition-metal tellurides typically revealed R–R and strong T–R bonding interactions, whereas the R–Te interactions were usually considered as strongly polar or ionic [65,68,69,70,71,72,73,74,75,76,77,78,79]. An evaluation of the hitherto detected rare-earth transition-metal tellurides for the group 11 transition-metals (Table 3) demonstrates that both metal- and tellurium-rich tellurides have been identified for this group. In the next section, we will focus on the bonding motifs of the tellurium-rich rare-earth transition-metal tellurides, which should be assigned to the group of intermetallic compounds with polyanionic fragments combined with monoatomic cations.

4. Tendencies within Bonding Motifs in Compounds with Polyanionic Fragments Combined with Monoatomic Cations

The electronic structures of the tellurium-rich (≥50 at.-% Te) tellurides are frequently illustrated by applying the Zintl–Klemm concept assuming that the valence electrons are formally transferred from the more electropositive to the more electronegative elements, which assemble fragments (Zintl anions) being isostructural to the modifications of isoelectronic elements [23,113,114]. For instance, in the crystal structure of Rb₂Te₂, the tellurium atoms assemble dumbbells, [Te₂]²⁻ (Figure 3a), which are isoelectronic to halide dumbbells based on a formal electron transfer from rubidium to tellurium after applying the Zintl–Klemm concept [80,114]. Furthermore, the electronic structures of certain telluride fragments in the crystal structures of tellurium-rich tellurides are understood by extending the Zintl–Klemm concept under consideration of the presence of hypervalent bonds [14,115]. One telluride that may serve as a prototypical example is TlTe, in which tellurium atoms attached as “handles” to linear tellurium chains form three-center four-electron hypervalent bonds with the central tellurium atoms within the aforesaid chains (Figure 3b) [14]. Although the Zintl–Klemm concept and its modified form considering the presence of hypervalent bonds facilitate the descriptions of the nature of bonding in the telluride fragments in several tellurium-rich tellurides, the applications of the Zintl–Klemm concept to the tellurium fragments in the crystal structures of certain different tellurium-rich tellurides result in the assignments of non-electron-precise charges to the tellurium atoms in the low-dimensional building units. In the following, we will review three examples of such tellurides [14].

LaCu_xTe₂ (0.28 ≤ x ≤ 0.50) and Gd₃Cu₂Te₇ are both tellurides whose crystal structures comprise linear undistorted tellurium chains (Figure 4) [87,88,89,98]. The occurrence of such undistorted linear tellurium chains is noteworthy, because low-dimensional tellurium building units, largely in the forms of tellurium square nets, often undergo structural distortions due to the formations of charge density waves [116,117,118,119,120,121]. Corresponding to the formations of charge density waves, the structural distortions in low-dimensional structural fragments are associated with the openings of band gaps at the Fermi levels, which reduce the electronic energies relative to those of the metallic states and, hence, alleviate electronic instabilities below certain transition temperatures [122,123]. Notably, the measurements of the temperature-dependent electrical conductivity behavior for LaCu_xTe₂ (0.28 ≤ x ≤ 0.50) revealed that this telluride should be a semiconductor [88,89]. Additional inspections of the X-ray diffraction patterns of SmCu_0.34Te₂ being isostructural with LaCu_xTe₂ (0.28 ≤ x ≤ 0.50) bared the presence of weak reflections pointing to a superstructure along the direction of the linear tellurium chains. Recent quantum chemical examinations [124] on the nature of bonding in these rare-earth copper tellurides showed the paramount role of heteroatomic R–Te bonding for these materials; however, the degrees of distortions within the linear tellurium chains appear to be influenced by the amounts of copper in the tellurides: a gedankenexperiment demonstrates that the Te chains can distort, a gap opens at the Fermi level and the overall bonding is maximized as the copper content is reduced.

Another example of a telluride whose electronic structure cannot be categorized by applying the Zintl–Klemm concept is the mineral stützite, Ag_5−xTe₃, that crystallizes in a broad homogeneity range (1.44 ≤ x ≤ −0.25) [125]. The crystal structure of stützite is composed of interpenetrating bicapped hexagonal tellurium antiprisms, which encompass Te-centered tricapped trigonal silver prisms, such that the units are best depicted by the net formula [Te@Ag₉]@Te₁₄ (Figure 5). Furthermore, the silver atoms surround the tellurium atoms in the forms of diverse types of polyhedrons. Because each stützite unit cell comprises four tellurium dumbbells ([Te₂]²⁻), an application of the Zintl–Klemm concept to a composition of Ag_5.14Te₃ ≡ Ag₃₆Te₂₁ [125] leads to a formal electron distribution represented by the formula (Ag⁺)₃₆(Te²⁻)₁₃([Te₂]²⁻)₄(e⁻)₂. Although the crystal structure of the mineral stützite comprises features typically observed for Zintl phases, the experimentally determined homogeneity ranges of this telluride (see above) [125] clearly indicate certain electronic flexibilities such that even electron-poorer compositions relative to an electron-precise one of Ag_4.86Te₃ ≡ (Ag⁺)₃₄(Te²⁻)₁₃([Te₂]²⁻)₄ are achieved. Quantum chemical examinations [126] on the electronic structures of models approximating the actual crystal structure of stützite revealed that the Fermi level falls in a gap for the electron-precise Ag₃₄Te₂₁, while the Fermi levels in a silver-richer model and a silver-poorer model, i.e., Ag₃₆Te₂₁ and Ag₃₂Te₂₁, are located above and below a gap, respectively. A bonding analysis indicates that the bonding in this material is dominated by the heteroatomic Ag–Te interactions beside a clearly smaller amount of more bonding homoatomic Te–Te interactions. Even though one may expect a situation with a gap at the Fermi level to be electronically favorable, it is the attempt to achieve both an electronically favorable situation with a gap at the Fermi level, and the maximization of the overall bonding through the depopulations of antibonding Ag–Te states that appear to control the amounts and the distributions of silver in the tellurium network.

Recent research on intermetallic compounds composed of active metals (A = elements of the groups 1–3) and transition- (T = elements of the group 11) as well as post-transition-elements (M = elements of the groups 13–15) revealed the existence of several compounds comprising anionic clusters, which possess less valence electron counts and, hence, are electron-poorer relative to Zintl phases [1,5]. In particular, the valence electron concentrations of these intermetallic compounds position these materials close to the Hume–Rothery phases (Scheme 1; a selection of overviews about the Hume–Rothery and the Zintl concept has been provided in Table 1) [127]. These so-called electron-poor intermetallics are typically observed for active metal-poor binary and ternary compounds containing anionic clusters of transition- and/or post-transition metals, especially gold [5,127]. The tendency of gold to form these anionic clusters and to participate in homo- as well as heteroatomic bonding arises from the influence of relativistic effects [128,129,130,131] which result in a tighter binding of the 6s orbitals such that the 5d orbitals exhibit a less tight binding and more 6s–5d orbital mixing follows [5]. To provide an insight into the general bonding trends of such electron-poorer intermetallic compounds, we evaluated a survey of the average −ICOHP/bond values and their respective percentage contributions to the net bonding capacities which have hitherto been reported in the literature for several electron-poorer ternary intermetallic compounds composed of an active metal, gold and a post-transition-metal (a compilation of the −ICOHP/bond values and respective percentages to the net bonding capabilities has been provided in

Table 4. e/a ratios ^a, average −ICOHP/bond values and respective percentages to the net bonding capabilities of the Au–Au and post-transition-metal–post-transition-metal as well as Au–post-transition-metal interactions for diverse active-metal-poor intermetallics composed of an active metal (group one–three element), gold and a post-transition-metal. Details about the quantum chemical computations and the crystal structures may be extracted from the respective references.

Compound	e/a	Parent Compound Disordered?	Homoatomic Contacts		Heteroatomic Contacts		Ref.
			Ave. −ICOHP/Bond	%	Ave. −ICOHP/Bond	%
Compounds with Anionic Fragments in the Forms of 1D Tunnels in the Crystal Structures
EuAu5In	1.43	yes, EuAu5.0In1.0	Au–Au: 0.79	57.1	Au–In: 0.81	36.5	[139]
KAu3Ga2	1.67	yes, KAu3.1Ga1.9	Au–Au: 0.79	20.1	Au–Ga: 1.18	72.2	[140]
			Ga–Ga: 0.55	5.6
RbAu3Ga2	1.67	no	Au–Au: 0.66	17.7	Au–Ga: 1.17	75.4	[141]
			Ga–Ga: 0.53	5.7
Na0.5Au2Ga2	1.89	yes, Na0.6Au2Ga2	Au–Au: 1.00	10.2	Au–Ga: 1.31	80.9	[141]
			Ga–Ga: 0.63	6.5
K0.5Au2Ga2	1.89	yes, K0.6Au2Ga2	Au–Au: 0.97	8.5	Au–Ga: 1.64	85.7	[140]
			Ga–Ga: 0.51	4.4
Rb0.5Au2Ga2	1.89	yes, Rb0.6Au2Ga2	Au–Au: 1.02	9.9	Au–Ga: 1.43	83.1	[141]
			Ga–Ga: 0.62	5.9
NaAu2Ga4	2.14	no	Ga–Ga: 1.04	20.0	Au–Ga: 1.73	72.2	[142]
KAu2Ga4	2.14	yes, KAu2.2Ga3.8	Au–Au: 1.04	1.6	Au–Ga: 1.88	71.3	[140]
			Ga–Ga: 1.20	22.7
CsAu5Ga9	2.20	no	Au–Au: 0.59	2.7	Au–Ga: 1.42	78.8	[143]
			Ga–Ga: 0.48	16.2
Compds. with hexagonal diamond-type networks as anionic fragments in the crystal structures
Sr2Au7Zn2	1.36	yes, Sr2Au6(Au,Zn)3	Au–Au: 1.21	40.5	Au–Zn: 1.02	37.7	[133]
			Zn–Zn: 0.56	1.0
Sr2Au7Al2	1.55	yes, Sr2Au7.3Al1.7	Au–Au: 1.07	32.0	Au–Al: 1.65	43.0	[134]
			Al–Al: 1.26	2.4
SrAu5Al2	1.63	yes, SrAu5.05Al1.95	Au–Au: 1.01	32.0	Au–Al: 1.61	54.6	[134]
			Al–Al: 0.71	1.6
Sr2Au6Al3	1.73	yes, Sr2Au6.2Al2.8	Au–Au: 1.09	21.5	Au–Al: 1.68	50.0	[134]
			Al–Al: 1.56	7.7
SrAu4Al3	1.88	yes, SrAu4.1Al2.9	Au–Au: 0.93	17.0	Au–Al: 1.61	63.0	[134]
			Al–Al: 1.48	8.9
Compounds with Diverse (Types of) Polyhedrons Formed by the Anions in the Crystal Structures
K12Au21Sn4	1.32	no	Au–Au: 1.22	28.0	Au–Sn: 2.70	43.1	[144]
Na8Au11Ga6	1.48	yes, Na8Au10.1Ga6.9	Au–Au: 1.22	31.9	Au–Ga: 1.71	44.7	[145]
			Ga–Ga: 1.49	5.2
NaAu4Ga2	1.57	no	Au–Au: 1.20	27.9	Au–Ga: 1.61	65.0	[142]
			Ga–Ga: 0.51	1.2
Y3Au9Sb	1.77	no	Au–Au: 1.17	51.7	Au–Sb: 1.06	11.7	[146]
CaAu4Bi	1.83	yes, CaAu4.1Bi0.9	Au–Au: 1.40	57.5	Au–Bi: 0.54	22.2	[147]
EuAu6Al6	2.00	yes, EuAu6.1Al5.9	Au–Au: 0.88	11.6	Au–Al: 1.58	67.8	[148]
			Al–Al: 0.95	10.8
EuAu6Ga6	2.00	yes, EuAu6.2Ga5.8	Au–Au: 0.64	11.2	Au–Ga: 1.40	68.0	[148]
			Ga–Ga: 0.91	11.1
Na5Au10Ga16	2.03	no	Au–Au: 0.42	0.8	Au–Ga: 1.67	71.2	[142]
			Ga–Ga: 1.10	22.2
Y3Au7Sn3	2.15	no	Au–Au: 0.78	22.2	Au–Sn: 1.33	42.1	[149]
Gd3Au7Sn3	2.15	no	Au–Au: 0.78	21.9	Au–Sn: 1.31	41.1	[149]

^a The e/a ratios represent the valence electron concentrations, which are determined by dividing the sums of the valence electrons by the numbers of atoms, e.g., e/a (EuAu₅In) = (2 + 5 + 3) VEs/7 atoms = 1.43.

). The crystal structures of these intermetallic compounds comprise anionic fragments in the forms of one-dimensional tunnels, hexagonal-diamond-like networks or diverse (types of) polyhedrons, which will be described in the following (Figure 6 and Figure 7).

Because the crystal structures of some of the inspected active-metal-poor intermetallic compounds comprise atomic sites with positional and/or occupational disorders (Table 4), the electronic structures of these materials were examined for models which approximate the actual crystal structures and often correspond to the lowest total energies. Details regarding all structure determinations and the generations of the hypothetical models suited for the electronic structure computations may be extracted from the respective literature that has been compiled in Table 4. Furthermore, the presence of positionally and/or occupationally disordered atomic positions in the crystal structure of a given active-metal-poor compound has been denoted and the actual composition experimentally determined for the respective ternary intermetallic compound has been included in Table 4. Notably, the presence of positional and/or occupational disorders has been identified for the atomic sites in the crystal structures of diverse representatives from all of the three inspected groups of active-metal-poor ternary intermetallic compounds. In the crystal structures of the intermetallic compounds belonging to the first of the aforementioned three groups (Table 4), the gold atoms and the post-transition-metal atoms assemble networks comprising cages which encompass the active-metals and are stringed along a certain crystallographic direction in the forms of one-dimensional tunnels. The cages and the enclosed active-metals in the crystal structures of some representatives of this group are slightly shifted from the axes penetrating the tunnels parallel to a crystallographic direction such that the chains of the active-metals exhibit displacements differing from arrangements expected for perfect linear chains. The second group of the active-metal-poor ternary intermetallic compounds, which are composed of an active-metal, gold and a post-transition-element and were taken into consideration for the survey of the previously reported −ICOHP/bond values and their respective percentages to the net bonding capabilities, contains those materials whose crystal structures comprise hexagonal-diamond-fashioned gold networks. In particular, the voids in the hexagonal-diamond-fashioned gold networks, which have to date been observed for four different types of structure and diverse combinations of gold with active metals (Sr, Ba, or Eu) and post-transition-metals (Zn, Cd, Al, Ga, In, or Sn) [132,133,134,135,136,137,138], enclose the active-metal atoms or triangles composed of the gold and the post-transition-metal atoms.

The third group of active-metal-poor ternary intermetallic compounds that have previously been identified for the active-metal–gold–post-transition-metal systems and were considered for the compilation of reported −ICOHP/bond values and their respective percentage contributions to the total bonding capabilities comprises those compounds, in which the (formally) anionic components constitute polyhedrons encapsulating the active-metals and/or gold or post-transition-metal atoms. The spatial arrangements of the polyhedrons assembled by the (formally) anionic components in the crystal structures of these ternary intermetallic compounds hinder the assignments of them to one of the two aforementioned groups. In some of these ternary intermetallic compounds, the anionic constituents also establish different types of polyhedrons enclosing the active-metals, gold and/or post-transition-metal atoms. For instance, in the crystal structures of R₃Au₇Sn₃ (R = Y, Gd) and Y₃Au₉Sb, gold atoms constitute trigonal prisms and antiprisms encapsulating other gold atoms and the post-transition-metal atoms, respectively (in the Sb-containing compound, Au atoms also reside in certain Au₆ antiprisms), while the gold atoms and the post-transition-metal atoms establish icosahedrons, tetrahedral stars and europium-centered snub cubes in the crystal structures of EuAu_6.1Al_5.9 and EuAu_6.2Ga_5.8 that are both derived from the NaZn₁₃ type of structure. Networks of vertices-sharing tetrahedrons which are composed of gold and enclose the active-metal atoms and post-transition metal atoms have been identified for the crystal structures of the ternary K₁₂Au₂₁Sn₄ and the MgCu₂-type-derived CaAu₄Bi (note that the gold network of the former compound also encases certain extra gold atoms). The crystal structures of Na₈Au_10.1Ga_6.9, NaAu₄Ga₂ and Na₅Au₁₀Ga₁₆ contain diverse types of Na-centered polyhedrons constructed by the gold atoms and the post-transition-metal atoms, and, for the case of the latter compound, Ga-centered Au₆ prisms.

A comparison of the valence electron concentrations for the active-metal-poor (A) ternary intermetallic compounds containing gold (Au) and post-transition-elements (M; Table 4) reveals that the e/a ratios of these materials are positioned in ranges being similar to those expected for the Hume–Rothery phases [24]. In this context, it is remarkable that the Fermi levels in the active-metal-poor ternary intermetallic compounds often fall in or close to pseudogaps in the densities-of-states curves, hence, indicating electronically favorable situations for these materials; however, one should not forget that the crystal structures of some of the inspected compounds comprise positionally and/or occupationally disordered atomic sites such that the e/a ratios can slightly differ (detailed descriptions about the electronic structures may be extracted from the literature listed in Table 4). Because the A–Au/M interactions generally exhibit the smallest −ICOHP/bond values and, hence, correspond to significantly smaller percentage contributions to the net bonding capabilities relative to those of the Au/M–Au/M interactions, it can be inferred that the majority of the bonding interactions resides between the Au/M–Au/M contacts. Furthermore, one may expect that the maximizations of the Au/M–Au/M interactions providing the largest bond energies may play crucial roles in the assignments of atoms on specific atomic sites, particularly, for the reason that the order of elements in a given material is influenced by the bond energy as well as the site energy [1]. An inspection of the −ICOHP/bond values and the respective percentages to the net bonding capabilities for these Au/M–Au/M interactions bares that the interactions with the largest −ICOHP/bond values principally show the largest percentages to the total bonding capabilities (Table 4). Indeed, this outcome suggests a tendency to maximize overall bonding as a structure determining aspect. The largest −ICOHP/bond values originate from the heteroatomic Au–M interactions for most of the inspected compounds. For a few of the inspected compounds, the largest −ICOHP/bond values and the largest percentages to the net bonding capabilities arise from strong Au–Au interactions, which means that the roles of relativistic effects (see above) and the local atomic environments with short Au–Au contacts need to be considered.

5. Conclusions and Perspectives

In summary, the survey of the tendencies within the electronic band structures and the bonding motifs for the inspected compounds comprising polycationic fragments paired with anionic ligands or polyanionic units combined with monoatomic cations indicates that two general aspects appear to be important to systemically understand the electronic structures for these materials:

(a)

The Fermi levels in these materials are often located in pseudogaps or gaps of the band structures to accomplish electronically favorable situations—features that are also expected for Hume–Rothery [24] and Zintl [23] phases, respectively.

(b)

The largest proportions to the net bonding capabilities are frequently achieved for the interactions providing large bond energies such that the overall bonding is optimized for a given material. Among the possible contacts, the largest bond energies stem from the heteroatomic interactions for most of the inspected materials.

At this point, one may wonder how these prerequisites can be implemented in general instructions to predict the existence ranges of intermetallic compounds. An approach to forecast the existence ranges of unknown intermetallic compounds may come from the use of quantum chemical high-throughput procedures for the designs of new materials.

Because of the permanent developments of quantum chemical techniques and the accessible computational resources, the predictions of new intermetallic compounds for a rational planning of syntheses can be accomplished through the identifications of the energetically most favorable structure models for previously unknown compounds by means of quantum chemical methods. The very first approaches to predict the structural characteristics of unknown materials were based on maps for the estimations of crystal structures [150], and the investigations of energy landscapes to forecast the free energies of unknown compounds [151]. Contemporary strategies to predict the chemical and the physical properties of unknown materials employ first-principles-based methods for the high-throughput screenings of compound libraries with the aid of adequate descriptors which enable relationships between the computed microscopic and experimentally determined macroscopic features [152,153]. For instance, a library composed of 400 possible compounds was inspected for the theoretical stabilities of these materials in a first-principles-methods-based multi-step protocol, which starts with screenings for materials with the lowest total energies and inspections of their dynamic stabilities, to predict and discover previously unidentified 18-electron ABX materials [154]. Furthermore, several descriptors enable the predictions of physical properties for the accelerated discoveries of materials with the desired characteristics including topological insulators [155] or thermoelectrics [156]. Although the applications of the aforementioned quantum chemical techniques drastically enhance the discoveries of new solid-state materials with the desired features, the applicableness of these procedures to forecast the existence ranges of unknown complex intermetallics is limited to date. In addition, the determinations of the actual nature of bonding for many representatives of the broad family of intermetallic compounds still require the inspections of the electronic structures from case to case in the lack of general prescriptions.