Sliding Dynamics of Parallel Graphene Sheets: Effect of Geometry and Van Der Waals Interactions on Nano-Spring Behavior
Abstract
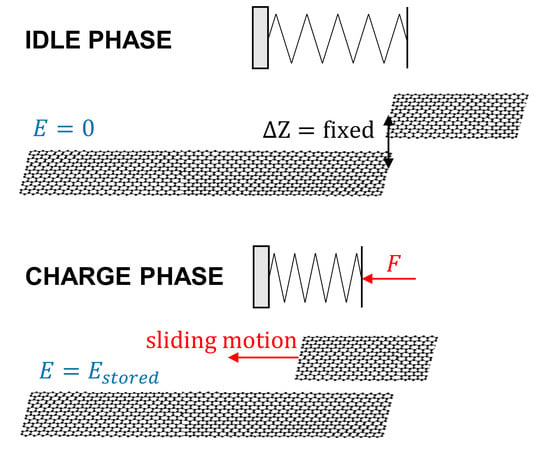
:1. Introduction
2. Methods
3. Results and Discussion
3.1. Atom–Atom Sliding
3.2. Atom–Chain Sliding
3.3. Chain–Chain Sliding
3.4. Sheet–Sheet Sliding
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A



References
- Bailey, S.W.D.; Amanatidis, I.; Lambert, C.J. Carbon nanotube electron windmills: A novel design for nanomotors. Phys. Rev. Lett. 2008, 100, 256802. [Google Scholar] [CrossRef] [PubMed]
- Laocharoensuk, R.; Burdick, J.; Wang, J. Carbon-nanotube-induced acceleration of catalytic nanomotors. ACS Nano 2008, 2, 1069–1075. [Google Scholar] [CrossRef] [PubMed]
- Hui, F.; Chen, S.; Liang, X.; Yuan, B.; Jing, X.; Shi, Y.; Lanza, M. Graphene Coated Nanoprobes: A Review. Crystals 2017, 7, 269. [Google Scholar] [CrossRef]
- Kazakova, O.; Panchal, V.; Burnett, T.L. Epitaxial graphene and graphene–based devices studied by electrical scanning probe microscopy. Crystals 2013, 3, 191–233. [Google Scholar] [CrossRef]
- Cumings, J.; Zettl, A. Localization and nonlinear resistance in telescopically extended nanotubes. Phys. Rev. Lett. 2004, 93, 086801. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, V.; Chiu, H.Y.; Postma, H.C.; Miko, C.; Forro, L.; Bockrath, M. Carbon nanotube linear bearing nanoswitches. Nano Lett. 2006, 6, 1092–1095. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.F.; Yakobson, B.I.; Ruoff, R.S. Controlled sliding and pullout of nested shells in individual multiwalled carbon nanotubes. J. Phys. Chem. B 2000, 104, 8764–8767. [Google Scholar] [CrossRef]
- Collins, P.G.; Arnold, M.S.; Avouris, P. Engineering carbon nanotubes and nanotube circuits using electrical breakdown. Science 2001, 292, 706–709. [Google Scholar] [CrossRef] [PubMed]
- Bigdeli, M.B.; Fasano, M. Thermal transmittance in graphene based networks for polymer matrix composites. Int. J. Therm. Sci. 2017, 117, 98–105. [Google Scholar] [CrossRef]
- Fasano, M.; Bigdeli, M.B.; Sereshk, M.R.V.; Chiavazzo, E.; Asinari, P. Thermal transmittance of carbon nanotube networks: Guidelines for novel thermal storage systems and polymeric material of thermal interest. Renew. Sustain. Energy Rev. 2015, 41, 1028–1036. [Google Scholar] [CrossRef]
- Fasano, M.; Bigdeli, M.B. Bottom up Approach Toward Prediction of Effective Thermophysical Properties of Carbon-Based Nanofluids. Heat Transf. Eng. 2017, 1–12. [Google Scholar] [CrossRef]
- Kis, A.; Jensen, K.; Aloni, S.; Mickelson, W.; Zettl, A. Interlayer Forces and Ultralow Sliding Friction in Multiwalled Carbon Nanotubes. Phys. Rev. Lett. 2006, 97, 025501. [Google Scholar] [CrossRef] [PubMed]
- Dienwiebel, M.; Verhoeven, G.S.; Pradeep, N.; Frenken, J.W.; Heimberg, J.A.; Zandbergen, H.W. Superlubricity of graphite. Phys. Rev. Lett. 2004, 92, 126101. [Google Scholar] [CrossRef] [PubMed]
- Dienwiebel, M.; Pradeep, N.; Verhoeven, G.S.; Zandbergen, H.W.; Frenken, J.W. Model experiments of superlubricity of graphite. Surf. Sci. 2005, 576, 197–211. [Google Scholar] [CrossRef]
- He, X.Q.; Kitipornchai, S.; Liew, K.M. Buckling analysis of multi-walled carbon nanotubes: A continuum model accounting for van der Waals interaction. J. Mech. Phys. Solids 2005, 53, 303–326. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 2000, 62, 104–110. [Google Scholar] [CrossRef]
- Cui, Z.; Guo, J.G. Theoretical investigations of the interfacial sliding and buckling of graphene on a flexible substrate. AIP Adv. 2016, 6, 125110. [Google Scholar] [CrossRef]
- Briggs, N.; Crossley, S. Rapid growth of vertically aligned multi-walled carbon nanotubes on a lamellar support. RSC Adv. 2015, 5, 83945–83952. [Google Scholar] [CrossRef]
- Krasnikov, D.; Shmakov, A.; Kuznetsov, V.; Ishchenko, A. Towards the optimization of carbon nanotube properties via in situ and ex situ studies of the growth mechanism. J. Struct. Chem. 2016, 57, 1436–1443. [Google Scholar] [CrossRef]
- Li, Y.j.; Ma, C.; Kang, J.l.; Shi, J.l.; Shi, Q.; Wu, D.h. Preparation of diameter-controlled multi-wall carbon nanotubes by an improved floating-catalyst chemical vapor deposition method. N. Carbon Mater. 2017, 32, 234–241. [Google Scholar] [CrossRef]
- Gallego, J.; Barrault, J.; Batiot-Dupeyrat, C.; Mondragon, F. Intershell spacing changes in MWCNT induced by metal–CNT interactions. Micron 2013, 44, 463–467. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.S.; Ren, W.; Gao, L.; Liu, B.; Jiang, C.; Cheng, H.M. Synthesis of high-quality graphene with a pre-determined number of layers. Carbon 2009, 47, 493–499. [Google Scholar] [CrossRef]
- Paton, K.R.; Varrla, E.; Backes, C.; Smith, R.J.; Khan, U.; O’Neill, A.; Boland, C.; Lotya, M.; Istrate, O.M.; King, P.; et al. Scalable production of large quantities of defect-free few-layer graphene by shear exfoliation in liquids. Nat. Mater. 2014, 13, 624. [Google Scholar] [CrossRef] [PubMed]
- Hadi, A.; Zahirifar, J.; Karimi-Sabet, J.; Dastbaz, A. Graphene nanosheets preparation using magnetic nanoparticle assisted liquid phase exfoliation of graphite: The coupled effect of ultrasound and wedging nanoparticles. Ultrason. Sonochem. 2018, 44, 204–214. [Google Scholar] [CrossRef]
- Delhaes, P. Graphite and Precursors; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Cumings, J.; Zettl, A. Low-Friction Nanoscale Linear Bearing Realized from Multiwall Carbon Nanotubes. Science 2000, 289, 602–605. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Hu, N.; Yamamoto, G.; Wang, Z.; Hashida, T.; Asanuma, H.; Dong, C.; Okabe, T.; Arai, M.; Fukunaga, H. Molecular mechanics simulation of the sliding behavior between nested walls in a multi-walled carbon nanotube. Carbon 2010, 48, 2934–2940. [Google Scholar] [CrossRef]
- Yamamoto, G.; Liu, S.; Hu, N.; Hashida, T.; Liu, Y.; Yan, C.; Li, Y.; Cui, H.; Ning, H.; Wu, L. Prediction of pull-out force of multi-walled carbon nanotube (MWCNT) in sword-in-sheath mode. Comput. Mater. Sci. 2012, 60, 7–12. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Guo, W.; Chen, C. Modifying atomic-scale friction between two graphene sheets: A molecular-force-field study. Phys. Rev. B 2007, 76, 155429. [Google Scholar] [CrossRef]
- Xia, Z.; Curtin, W.A. Pullout forces and friction in multiwall carbon nanotubes. Phys. Rev. B 2004, 69, 1–4. [Google Scholar] [CrossRef]
- Guo, W.; Gao, H. Optimized bearing and interlayer friction in multiwalled carbon nanotubes. CMES Comput. Model. Eng. Sci. 2005, 7, 19–34. [Google Scholar]
- Kimoto, Y.; Mori, H.; Mikami, T.; Akita, S.; Nakayama, Y.; Higashi, K.; Hirai, Y. Molecular Dynamics Study of Double-Walled Carbon Nanotubes for Nano-Mechanical Manipulation. Jpn. J. Appl. Phys. 2005, 44, 1641–1647. [Google Scholar] [CrossRef]
- Shakouri, A.; Yeo, J.; Ng, T.Y.; Liu, Z.; Taylor, H. Superlubricity-activated thinning of graphite flakes compressed by passivated crystalline silicon substrates for graphene exfoliation. Carbon 2014, 80, 68–74. [Google Scholar] [CrossRef]
- Sung, M.K.; Lee, S. The Effect of van der Waals Forces on the Exfoliation of Graphene Sheets from Graphite by Frictional Motion. J. Nanosci. Nanotechnol. 2016, 16, 11529–11534. [Google Scholar] [CrossRef]
- Tanaka, K.; Aoki, H. Interlayer interaction of two graphene sheets as a model of double-layer carbon nanotubes. Carbon 1997, 35, 121–125. [Google Scholar] [CrossRef]
- Silva, F.R.; Filho, E.D. Confined Lennard Jones potential: a variational treatment. Mod. Phys. Lett. A 2010, 25, 641–648. [Google Scholar] [CrossRef]
- Kaukonen, M.; Gulans, A.; Havu, P.; Kauppinen, E. Lennard-Jones parameters for small diameter carbon nanotubes and water for molecular mechanics simulations from van der Waals density functional calculations. J. Comput. Chem. 2012, 33, 652–658. [Google Scholar] [CrossRef] [PubMed]
- Kis, A.; Zettl, A. Nanomechanics of carbon nanotubes. Philos. Trans. R. Soc. A 2008, 366, 1591–1611. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Jiang, B.; Liu, S.; Weng, Y.; Lu, L.; Xue, Q.; Zhu, J.; Jiang, Q.; Wang, S.; Peng, L. Self-retracting motion of graphite microflakes. Phys. Rev. Lett. 2008, 100, 067205. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, S.M.; Yang, J.R.; Liu, J.Z.; Yang, Y.L.; Zheng, Q.S. Interlayer shear strength of single crystalline graphite. Acta Mech. Sin. 2012, 28, 978–982. [Google Scholar] [CrossRef]
- Cote, L.J.; Kim, F.; Huang, J. Langmuir- Blodgett assembly of graphite oxide single layers. J. Am. Chem. Soc. 2008, 131, 1043–1049. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Cao, T.; Cellini, F.; Berger, C.; de Heer, W.A.; Tosatti, E.; Riedo, E.; Bongiorno, A. Ultrahard carbon film from epitaxial two-layer graphene. Nat. Nanotechnol. 2018, 13, 133. [Google Scholar] [CrossRef] [PubMed]
- Elibol, K.; Bayer, B.C.; Hummel, S.; Kotakoski, J.; Argentero, G.; Meyer, J.C. Visualising the strain distribution in suspended two-dimensional materials under local deformation. Sci. Rep. 2016, 6, 28485. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Ryu, S.; Kim, D.K.; Woo, W.; Sohn, D. Effect of interlayer sliding on the estimation of elastic modulus of multilayer graphene in nanoindentation simulation. EPL (Europhys. Lett.) 2016, 114, 68001. [Google Scholar] [CrossRef]
- Xiang, L.; Ma, S.Y.; Wang, F.; Zhang, K. Nanoindentation models and Young’s modulus of few-layer graphene: A molecular dynamics simulation study. J. Phys. D Appl. Phys. 2015, 48, 395305. [Google Scholar] [CrossRef]






| (nm) | (nm) | |||
|---|---|---|---|---|
| 2 | 3 | 0.568 | 0.738 | 28 |
| 2 | 4 | 0.568 | 0.984 | 36 |
| 2 | 5 | 0.568 | 1.230 | 44 |
| 3 | 4 | 0.994 | 0.984 | 54 |
| 3 | 5 | 0.994 | 1.230 | 66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crisafulli, A.; Khodayari, A.; Mohammadnejad, S.; Fasano, M. Sliding Dynamics of Parallel Graphene Sheets: Effect of Geometry and Van Der Waals Interactions on Nano-Spring Behavior. Crystals 2018, 8, 149. https://doi.org/10.3390/cryst8040149
Crisafulli A, Khodayari A, Mohammadnejad S, Fasano M. Sliding Dynamics of Parallel Graphene Sheets: Effect of Geometry and Van Der Waals Interactions on Nano-Spring Behavior. Crystals. 2018; 8(4):149. https://doi.org/10.3390/cryst8040149
Chicago/Turabian StyleCrisafulli, Alessandro, Ali Khodayari, Shahin Mohammadnejad, and Matteo Fasano. 2018. "Sliding Dynamics of Parallel Graphene Sheets: Effect of Geometry and Van Der Waals Interactions on Nano-Spring Behavior" Crystals 8, no. 4: 149. https://doi.org/10.3390/cryst8040149
APA StyleCrisafulli, A., Khodayari, A., Mohammadnejad, S., & Fasano, M. (2018). Sliding Dynamics of Parallel Graphene Sheets: Effect of Geometry and Van Der Waals Interactions on Nano-Spring Behavior. Crystals, 8(4), 149. https://doi.org/10.3390/cryst8040149