The Role of Hyperconjugation on the Structure and C–H Stretching Frequencies of 3,3′-Ethane-1,2-diyl- bis-1,3,5-triazabicyclo[3.2.1]octane (ETABOC): An X-Ray Structure and Vibrational Study
Abstract
:1. Introduction

2. Materials and Methods
2.1. X-Ray Analysis
2.2. Theoretical Calculations
3. Results and Discussion
3.1. Conformational Analysis
3.2. Infrared Spectrum
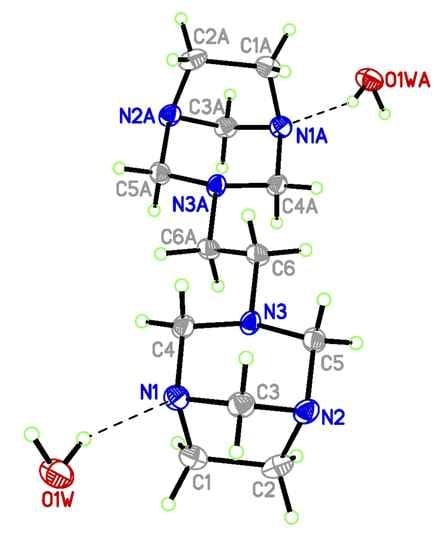
3.3. Single Crystal X-Ray Diffraction
3.4. NBO Analysis
3.5. NMR
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Böhme, H. α-Halogenierte anzine und ihre umsetzungen. Angew. Chem. 1956, 68, 33–34. [Google Scholar] [CrossRef]
- Rivera, A.; Ríos-Motta, J. An unusual product obtained from condensation between ethylenediamine and formaldehyde in basic medium. Tetrahedron Lett. 2005, 46, 5001–5004. [Google Scholar] [CrossRef]
- Hamlow, H.P.; Okuda, S.; Nakagawa, N. NMR effects of cyclic tertiary amines. Tetrahedron Lett. 1964, 5, 2553–2559. [Google Scholar] [CrossRef]
- Gogoll, A.; Grennberg, H.; Axén, A. Chemical shift assignment of geminal protons in 3,7-diazabicyclo[3.3.1]nonanes: An unexpected deviation from the axial/equatorial chemical shift order. Magn. Reson. Chem. 1997, 35, 13–20. [Google Scholar] [CrossRef]
- Pandiarajan, K.; Manimekalai, A.; Rajarajan, G. 1H NMR spectral study of some 4-hydroxy-2,6-diphenylpiperidines and a systematic analysis of 1H chemical shifts in some piperidines and 3,7-diazabicyclo[3.3.1]nonane derivatives. Indian J. Chem. B 2000, 398, 517–524. [Google Scholar] [CrossRef]
- Albright, T.A.; Burdett, J.K.; Whangbo, M.H. Orbital Interactions through space and through bonds. In Orbital Interactions in Chemistry, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Zwier, J.M.; Brouwer, A.M.; Keszthelyi, T.; Balakrishnan, G.; Offersgaard, J.F.; Wilbrandt, R.; Barbosa, F.; Buser, U.; Amaudrut, J.; Gescheidt, G.; et al. Electron delocalization in the radical cation of 1,3,6,8-tetraazatricyclo[4.4.1.13,8]dodecane, a 4-nitrogen-7-electron system. J. Am. Chem. Soc. 2002, 124, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Brodskaya, E.I.; Ratovskii, G.V.; Voronkov, M.G. Orbital interactions through space and through σ-bonds. Russ. Chem. Rev. 1993, 62, 919–933. [Google Scholar] [CrossRef]
- Hoffmann, R. Interaction of orbitals through space and through bonds. Acc. Chem. Res. 1971, 4, 1–9. [Google Scholar] [CrossRef]
- Jiang, L.; Orimoto, Y.; Aoki, Y. Stereoelectronic effects in Menshutkin-type SN2 reactions: Theoretical study based on through-space/bond orbital interaction analysis. J. Phys. Org. Chem. 2013, 26, 885–891. [Google Scholar] [CrossRef]
- Ohno, K.; Ishida, T.; Naitoh, Y.; Izumi, Y. Study of stereochemical properties of molecular orbitals by Penning ionization electron spectroscopy. Effects of through-space/through-bond interactions on electron distributions. J. Am. Chem. Soc. 1985, 107, 8082–8086. [Google Scholar] [CrossRef]
- Werstiuk, N.H.; Butler, D.N.; Datta, S. A study of lone-pair interactions of tetracyclic diamines by ultraviolet photoelectron spectroscopy. Can. J. Chem. 1986, 64, 760–763. [Google Scholar] [CrossRef] [Green Version]
- Heilbronner, E.; Muszkat, K.A. Applications of photoelectron spectroscopy. X. Relative importance of through-space vs. through-bond interaction between the lone pairs in 1,4-diazabicyclo[2.2.2]octane. J. Am. Chem. Soc. 1970, 92, 3818–3821. [Google Scholar] [CrossRef]
- Stoe & Cie. X-Area Diffractometer Control Software; Stoe & Cie: Darmstadt, Germany, 2001. [Google Scholar]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. 2009, 65, 148–155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A.; Vreven, T., Jr.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03; Gaussian, Inc.: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO Version 3.1; Tcl University of Wisconsin: Madison, WI, USA, 1998. [Google Scholar]
- Ditchfield, R. Molecular orbital theory of magnetic shielding and magnetic susceptibility. J. Chem. Phys. 1972, 56, 5688–5691. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Kolmer, A.; Edwards, L.J.; Kuprov, I.; Thiele, C.M. Conformational analysis of small organic molecules using NOE and RDC data: A discussion of strychnine and α-methylene-γ-butyrolactone. J. Magn. Reson. 2015, 261, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Neuhaus, D.; Williamson, M.P. The Nuclear Overhauser Effect in Structural and Conformational Analysis, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Kwan, E.E.; Huang, S.G. Structural elucidation with NMR spectroscopy: Practical strategies for organic chemists. Eur. J. Org. Chem. 2008, 2008, 2671–2688. [Google Scholar] [CrossRef]
- Gribble, W.G.; Nelson, R.B. Conformational requirements for the existence of Bohlmann bands in the infrared spectra of indolo[2,3-a]quinolizidines. I. Cis- and trans-2-tert-butyl derivatives. J. Org. Chem. 1973, 38, 2831–2864. [Google Scholar] [CrossRef]
- Nasipuri, D. Stereochemistry of Organic Compounds: Principles and Applications; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Jeyaraman, R.; Ravindran, T.; Sujatha, M.; Venkatraj, M. Lowering of Bohlmann band intensities in conformationally homogeneous 2,6-diarylpiperidines due to ring distortion. Indian J. Chem. B 1999, 38, 52–55. [Google Scholar] [CrossRef]
- Bertrand, B.; Nisole, C.; Drancourt, J.M.; Dubuffet, T.; Bouchet, J.P.; Volland, J.P. Determination of cis and trans configurations in pentahydrobenzopyranopyrroles by FT-IR spectroscopy. Spectrochim. Acta A 1996, 52, 1921–1923. [Google Scholar] [CrossRef]
- Garraffo, H.M.; Simon, L.D.; Daly, J.W.; Spande, T.F.; Jones, T.H. Cis- and trans-configurations of α,α′-disubstituted piperidines and pyrrolidines by GC-FTIR; application to decahydroquinoline stereochemistry. Tetrahedron 1994, 50, 11329–11338. [Google Scholar] [CrossRef]
- Wolfe, S.; Schlegel, H.B.; Whangbo, M.H.; Bernardi, F. On the origin of the Bohlmann bands. Can. J. Chem. 1974, 52, 3787–3792. [Google Scholar] [CrossRef]
- Demaison, J.; Margulès, L.; Boggs, J.E. The equilibrium N–H bond length. Chem. Phys. 2000, 260, 65–81. [Google Scholar] [CrossRef]
- Pinto, B.M.; Schlegel, H.B.; Wolfe, S. Bond angle variations in XCY fragments and their relationship to the anomeric effect. Can. J. Chem. 1987, 65, 1658–1662. [Google Scholar] [CrossRef] [Green Version]
- Allen, F.H.; Kennard, O.; Watson, D.G.; Brammer, L.; Orpen, A.G.; Taylor, R. Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J. Chem. Soc. Perkin Trans. 2 1987, 12, S1–S19. [Google Scholar] [CrossRef]
- Alabugin, I.V.; Zeidan, T.A. Stereoelectronic effects and general trends in hyperconjugative acceptor ability of σ bonds. J. Am. Chem. Soc. 2002, 124, 3175–3185. [Google Scholar] [CrossRef] [PubMed]







| Compound | |
|---|---|
| CCDC No. | 1522802 |
| Empirical formula | C12H28N6O2 |
| Formula weight | 288.40 |
| Temperature | 173(2) K |
| Crystal system | monoclinic |
| Space group | P21/n |
| Unit cell dimensions | a = 5.8765(9) Å, α = 90° |
| b = 6.9967(10) Å, β = 95.642(14)° | |
| c = 18.240(3) Å, γ = 90° | |
| Volume | 746.3(2) Å3 |
| Z | 2 |
| Calculated density | 1.283 g/cm3 |
| Absorption coefficient | 0.091 mm−1 |
| F(000) | 316 |
| Crystal size mm3 | 0.17 × 0.14 × 0.06 |
| θmin/θmax/° | 3.554/25.608 |
| Limiting indices | −7 ≤ h ≤ 7, −8 ≤ k ≤ 8, −22 ≤ l ≤ 22 |
| Reflections collected | 5748 |
| Independent reflections | 1396 [R(int) = 0.0725] |
| Refinement method | Full-matrix least-squares on F2 |
| Data/restraints/parameters | 1396/0/101 |
| Goodness of fit on F2 | 1.250 |
| R1/wR2[I > 2σ(I)] | 0.0830/0.1700 |
| R1/wR2(all data) | 0.1007/0.1750 |
| Largest diff. peak and hole/e.Å−1 | 0.244/−0.300 |
| ∆E, kcal/mol | ϕ1 | ϕ2 | ϕ3 | ϕ4 | ϕ5 | |
|---|---|---|---|---|---|---|
| 4 | 15.9 | 180.0 | −153.79 | 71.72 | −71.72 | 153.79 |
| 5 | 0.0 | −180.0 | 161.70 | −74.35 | 74.35 | −161.68 |
| Parameter a | Exp. b | Theor. c | Theor. d |
|---|---|---|---|
| N(1)-C(1) | 1.491(5) | 1.483 | 1.468 |
| N(1)-C(3) | 1.474(5) | 1.474 | 1.456 |
| N(1)-C(4) | 1.462(5) | 1.465 | 1.451 |
| N(2)-C(2) | 1.488(5) | 1.483 | 1.468 |
| N(2)-C(3) | 1.471(5) | 1.474 | 1.456 |
| N(2)-C(5) | 1.477(5) | 1.464 | 1.450 |
| N(3)-C(4) | 1.481(4) | 1.473 | 1.459 |
| N(3)-C(5) | 1.465(5) | 1.473 | 1.459 |
| N(3)-C(6) | 1.463(5) | 1.459 | 1.450 |
| C(1)-C(2) | 1.556(6) | 1.574 | 1.561 |
| C(6)-C(6)#1 | 1.526(7) | 1.537 | 1.529 |
| C(3)-N(1)-C(1) | 100.9(3) | 100.8 | 101.2 |
| C(4)-N(1)-C(1) | 110.2(3) | 110.8 | 111.2 |
| C(4)-N(1)-C(3) | 107.4(3) | 107.5 | 108.0 |
| C(3)-N(2)-C(2) | 100.5(3) | 100.8 | 101.2 |
| C(5)-N(2)-C(2) | 110.1(3) | 110.9 | 111.2 |
| C(3)-N(2)-C(5) | 107.1(3) | 107.3 | 107.9 |
| C(5)-N(3)-C(4) | 110.3(3) | 110.9 | 111.9 |
| C(6)-N(3)-C(4) | 111.8(3) | 114.2 | 114.3 |
| C(6)-N(3)-C(5) | 111.4(3) | 112.8 | 113.2 |
| Entry | Donor (i) | Type | Acceptor (j) | Type | E2(kcal/mol) |
|---|---|---|---|---|---|
| 1 | N(1) | lp | C4–N3 | σ* | 9.02 |
| C3–N2 | 6.59 | ||||
| C1–C2 | 4.78 | ||||
| C1–H1exo | 3.17 | ||||
| C3–H3anti | 1.79 | ||||
| C4–H4endo | 1.55 | ||||
| C4–H4exo | 0.97 | ||||
| 2 | N(2) | lp | C5–N3 | σ* | 9.01 |
| C3–N1 | 6.55 | ||||
| C1–C2 | 4.75 | ||||
| C2–H2exo | 3.19 | ||||
| C3–H3anti | 1.79 | ||||
| C5–H5endo | 1.58 | ||||
| 3 | N(3) | lp | C6–H6a | σ* | 7.54 |
| C5–H5exo | 7.38 | ||||
| C4–H4exo | 7.33 | ||||
| C5–H5endo | 2.07 | ||||
| C4–H4endo | 2.05 | ||||
| C6–C6′ | 2.05 | ||||
| C5–N2 | 1.15 | ||||
| C4–N1 | 1.13 |
| Ci | C2v | C2 | Exp. | |
|---|---|---|---|---|
| C-4 | 77.5 | 78.8 | 79.5 | 76.5 |
| C-5 | 80.3 | 80.0 | 80.7 | 76.5 |
| C-2 | 54.5 | 54.9 | 59.3 | 51.9 |
| C-1 | 54.8 | 54.8 | 59.0 | 51.9 |
| C-3 | 78.5 | 78.1 | 78.3 | 76.6 |
| C-6 | 52.3 | 54.0 | 49.3 | 48.5 |
| C-4′ | 77.7 | 78.9 | 79.6 | 76.5 |
| C-5′ | 80.3 | 79.8 | 80.5 | 76.5 |
| C-2′ | 54.6 | 54.8 | 59.2 | 51.9 |
| C-1′ | 55.0 | 54.9 | 59.1 | 51.9 |
| C-3′ | 78.5 | 78.1 | 78.3 | 76.6 |
| C-6′ | 53.4 | 53.8 | 49.4 | 48.5 |
| H-4endo | 3.68 | 3.48 | 3.72 | 3.62 |
| H-4exo | 3.29 | 3.50 | 3.70 | 3.40 |
| H-5endo | 3.45 | 3.46 | 3.68 | 3.62 |
| H-5exo | 3.46 | 3.49 | 3.69 | 3.40 |
| H-2endo | 3.09 | 3.09 | 5.78 | 3.17 |
| H-2exo | 2.73 | 2.64 | 2.93 | 2.79 |
| H-1endo | 3.04 | 3.09 | 5.72 | 3.17 |
| H-1exo | 2.71 | 2.63 | 2.92 | 2.79 |
| H-3syn | 3.65 | 3.66 | 3.68 | 3.89 |
| H-3anti | 3.26 | 3.25 | 3.27 | 3.30 |
| H-6a | 1.96 | 1.69 | 1.74 | 2.17 |
| H-6b | 1.99 | 1.95 | 1.96 | 2.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivera, A.; Uribe, J.M.; Ríos-Motta, J.; Bolte, M. The Role of Hyperconjugation on the Structure and C–H Stretching Frequencies of 3,3′-Ethane-1,2-diyl- bis-1,3,5-triazabicyclo[3.2.1]octane (ETABOC): An X-Ray Structure and Vibrational Study. Crystals 2018, 8, 251. https://doi.org/10.3390/cryst8060251
Rivera A, Uribe JM, Ríos-Motta J, Bolte M. The Role of Hyperconjugation on the Structure and C–H Stretching Frequencies of 3,3′-Ethane-1,2-diyl- bis-1,3,5-triazabicyclo[3.2.1]octane (ETABOC): An X-Ray Structure and Vibrational Study. Crystals. 2018; 8(6):251. https://doi.org/10.3390/cryst8060251
Chicago/Turabian StyleRivera, Augusto, Juan Manuel Uribe, Jaime Ríos-Motta, and Michael Bolte. 2018. "The Role of Hyperconjugation on the Structure and C–H Stretching Frequencies of 3,3′-Ethane-1,2-diyl- bis-1,3,5-triazabicyclo[3.2.1]octane (ETABOC): An X-Ray Structure and Vibrational Study" Crystals 8, no. 6: 251. https://doi.org/10.3390/cryst8060251
APA StyleRivera, A., Uribe, J. M., Ríos-Motta, J., & Bolte, M. (2018). The Role of Hyperconjugation on the Structure and C–H Stretching Frequencies of 3,3′-Ethane-1,2-diyl- bis-1,3,5-triazabicyclo[3.2.1]octane (ETABOC): An X-Ray Structure and Vibrational Study. Crystals, 8(6), 251. https://doi.org/10.3390/cryst8060251