Surface Anchoring Effects on the Formation of Two-Wavelength Surface Patterns in Chiral Liquid Crystals
Abstract
:1. Introduction
2. Geometry and Structure
3. Governing Equations
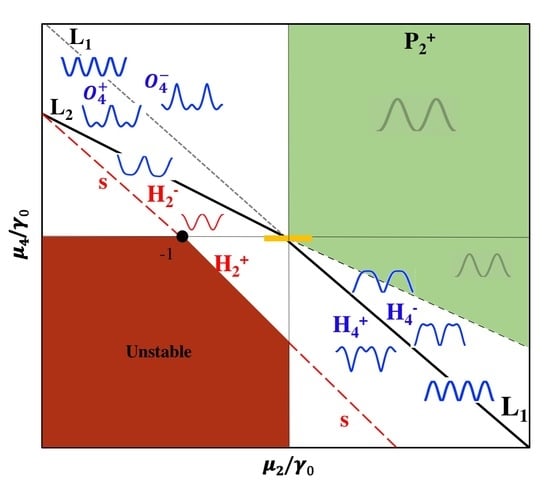
4. Results and Discussion
4.1. Surface Profile
4.2. Surface Curvature
4.3. Surface Energy
4.4. Capillary Pressures
4.5. Capillary Vectors
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Cahn-Hoffman Capillary Vector

Appendix B. Capillary Pressures
Appendix C. Governing Equation
Appendix D. Linear Theory
Appendix E. Relations
Appendix F. Capillary Vectors
References
- Vignolini, S.; Moyroud, E.; Glover, B.J.; Steiner, U. Analysing photonic structures in plants. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Willcox, P.J.; Gido, S.P.; Muller, W.; Kaplan, D.L. Evidence of a cholesteric liquid crystalline phase in natural silk spinning processes. Macromolecules 1996, 29, 5106–5110. [Google Scholar] [CrossRef]
- Sharma, V.; Crne, M.; Park, J.O.; Srinivasarao, M. Structural Origin of Circularly Polarized Iridescence in Jeweled Beetles. Science 2009, 325, 449–451. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.L.; Wong, D.; Lee, P. Iridescence of a shell of mollusk Haliotis Glabra. Opt. Express 2004, 12, 4847–4854. [Google Scholar] [CrossRef] [PubMed]
- Parker, A.R. Discovery of functional iridescence and its coevolution with eyes in the phylogeny of Ostracoda (Crustacea). Proc. R. Soc. B Biol. Sci. 1995, 262, 349–355. [Google Scholar]
- Parker, A.R.; Martini, N. Diffraction Gratings in Caligoid (Crustacea: Copepoda) Ecto-parasites of Large Fishes. Mater. Today: Proc. 2014, 1, 138–144. [Google Scholar] [CrossRef]
- Sharma, V.; Crne, M.; Park, J.O.; Srinivasarao, M. Bouligand Structures Underlie Circularly Polarized Iridescence of Scarab Beetles: A Closer View. Mater. Today: Proc. 2014, 1, 161–171. [Google Scholar] [CrossRef]
- Vukusic, P.; Sambles, J.R.; Lawrence, C.R. Structural colour—Colour mixing in wing scales of a butterfly. Nature 2000, 404, 457. [Google Scholar] [CrossRef]
- Gould, K.S.; Lee, D.W. Physical and ultrastructural basis of blue leaf iridescence in four Malaysian understory plants. Am. J. Bot. 1996, 83, 45–50. [Google Scholar] [CrossRef]
- Graham, R.M.; Lee, D.W.; Norstog, K. Physical and Ultrastructural Basis of Blue Leaf Iridescence in 2 Neotropical Ferns. Am. J. Bot. 1993, 80, 198–203. [Google Scholar] [CrossRef]
- Whitney, H.M.; Kolle, M.; Andrew, P.; Chittka, L.; Steiner, U.; Glover, B.J. Floral Iridescence, Produced by Diffractive Optics, Acts As a Cue for Animal Pollinators. Science 2009, 323, 130–133. [Google Scholar] [CrossRef] [PubMed]
- Urbanski, M.; Reyes, C.G.; Noh, J.; Sharma, A.; Geng, Y.; Jampani, V.S.R.; Lagerwall, J.P.F. Liquid crystals in micron-scale droplets, shells and fibers. J. Phys. Condens. Matter 2017, 29, 133003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitov, M. Cholesteric liquid crystals in living matter. Soft Matter 2017, 13, 4176–4209. [Google Scholar] [CrossRef] [PubMed]
- Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402–3429. [Google Scholar] [CrossRef]
- Bouligan, Y. Twisted Fibrous Arrangements in Biological-Materials and Cholesteric Mesophases. Tissue Cell 1972, 4, 189–217. [Google Scholar] [CrossRef]
- Neville, A.C. Biology of Fibrous Composites: Development Beyond the Cell Membrane; Cambridge University Press: New York, NY, USA, 1993; p. vii. 214p. [Google Scholar]
- Rey, A.D.; Herrera-Valencia, E.E.; Murugesan, Y.K. Structure and dynamics of biological liquid crystals. Liq. Cryst. 2014, 41, 430–451. [Google Scholar] [CrossRef]
- Rey, A.D.; Herrera-Valencia, E.E. Liquid crystal models of biological materials and silk spinning. Biopolymers 2012, 97, 374–396. [Google Scholar] [CrossRef]
- Murugesan, Y.K.; Pasini, D.; Rey, A.D. Self-assembly Mechanisms in Plant Cell Wall Components. J. Renew. Mater. 2015, 3, 56–72. [Google Scholar] [CrossRef]
- Canejo, J.P.; Monge, N.; Echeverria, C.; Fernandes, S.N.; Godinho, M.H. Cellulosic liquid crystals for films and fibers. Liq. Cryst. Rev. 2017, 5, 86–110. [Google Scholar] [CrossRef]
- Rofouie, P.; Alizadehgiashi, M.; Mundoor, H.; Smalyukh, I.I.; Kumacheva, E. Self-Assembly of Cellulose Nanocrystals into Semi-Spherical Photonic Cholesteric Films. Adv. Funct. Mater. 2018, 28. [Google Scholar] [CrossRef]
- Rofouie, P.; Pasini, D.; Rey, A.D. Nano-scale surface wrinkling in chiral liquid crystals and plant-based plywoods. Soft Matter 2015, 11, 1127–1139. [Google Scholar] [CrossRef] [PubMed]
- Rofouie, P.; Pasini, D.; Rey, A.D. Nanostructured free surfaces in plant-based plywoods driven by chiral capillarity. Colloids Interface Sci. Commun. 2014, 1, 23–26. [Google Scholar] [CrossRef] [Green Version]
- Rofouie, P.; Pasini, D.; Rey, A.D. Tunable nano-wrinkling of chiral surfaces: Structure and diffraction optics. J. Chem. Phys. 2015, 143, 114701. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, S.N.; Geng, Y.; Vignolini, S.; Glover, B.J.; Trindade, A.C.; Canejo, J.P.; Almeida, P.L.; Brogueira, P.; Godinho, M.H. Structural Color and Iridescence in Transparent Sheared Cellulosic Films. Macromol. Chem. Phys. 2013, 214, 25–32. [Google Scholar] [CrossRef]
- Sharon, E.; Roman, B.; Marder, M.; Shin, G.S.; Swinney, H.L. Mechanics: Buckling cascades in free sheets—Wavy leaves may not depend only on their genes to make their edges crinkle. Nature 2002, 419, 579. [Google Scholar] [CrossRef]
- Aharoni, H.; Abraham, Y.; Elbaum, R.; Sharon, E.; Kupferman, R. Emergence of Spontaneous Twist and Curvature in Non-Euclidean Rods: Application to Erodium Plant Cells. Phys. Rev. Lett. 2012, 108, 238106. [Google Scholar] [CrossRef]
- Rofouie, P.; Pasini, D.; Rey, A.D. Multiple-wavelength surface patterns in models of biological chiral liquid crystal membranes. Soft Matter 2017, 13, 541–545. [Google Scholar] [CrossRef]
- Rofouie, P.; Pasini, D.; Rey, A.D. Morphology of elastic nematic liquid crystal membranes. Soft Matter 2017, 13, 5366–5380. [Google Scholar] [CrossRef]
- Rofouie, P.; Wang, Z.; Rey, A.D. Two-wavelength wrinkling patterns in helicoidal plywood surfaces: Imprinting energy landscapes onto geometric landscapes. Soft Matter 2018, 14, 5180–5185. [Google Scholar] [CrossRef]
- Cheong, A.G.; Rey, A.D. Cahn-Hoffman capillarity vector thermodynamics for curved liquid crystal interfaces with applications to fiber instabilities. J. Chem. Phys. 2002, 117, 5062–5071. [Google Scholar] [CrossRef]
- Rapini, A.; Papoular, M. Distorsion d’une lamelle nématique sous champ magnétique conditions d’ancrage aux parois. J. Phys. Colloq. 1969, 30, C4-54–C4-56. [Google Scholar] [CrossRef]
- Rey, A.D. Capillary models for liquid crystal fibers, membranes, films, and drops. Soft Matter 2007, 3, 1349–1368. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Shmeliova, D.V.; Semenov, S.V. Towards the restoration of the liquid crystal surface anchoring potential using Grandgean-Cano wedge. Mol. Cryst. Liq. Cryst. 2017, 657, 34–45. [Google Scholar] [CrossRef]
- Rey, A.D. Nemato-capillarity theory and the orientation-induced Marangoni flow. Liq. Cryst. 1999, 26, 913–917. [Google Scholar] [CrossRef]
- Rey, A.D. Marangoni flow in liquid crystal interfaces. J. Chem. Phys. 1999, 110, 9769–9770. [Google Scholar] [CrossRef]
- Eelkema, R.; Pollard, M.M.; Katsonis, N.; Vicario, J.; Broer, D.J.; Feringa, B.L. Rotational reorganization of doped cholesteric liquid crystalline films. J. Am. Chem. Soc. 2006, 128, 14397–14407. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.G.; Li, J.; Forest, M.G.; Wang, Q. Hydrodynamic Theories for Flows of Active Liquid Crystals and the Generalized Onsager Principle. Entropy 2016, 18, 202. [Google Scholar] [CrossRef]
- Forest, M.G.; Wang, Q.; Zhou, R.H. Kinetic theory and simulations of active polar liquid crystalline polymers. Soft Matter 2013, 9, 5207–5222. [Google Scholar] [CrossRef]
- Brand, H.R.; Pleiner, H.; Svensek, D. Dissipative versus reversible contributions to macroscopic dynamics: The role of time-reversal symmetry and entropy production. Rheol. Acta 2018, 57, 773–791. [Google Scholar] [CrossRef]
- Rey, A.D. Theory of linear viscoelasticity of chiral liquid crystals. Rheol. Acta 1996, 35, 400–409. [Google Scholar] [CrossRef]
- Rey, A.D. Theory of linear viscoelasticity of cholesteric liquid crystals. J. Rheol. 2000, 44, 855–869. [Google Scholar] [CrossRef]
- Hoffman, D.W.; Cahn, J.W. Vector Thermodynamics for Anisotropic Surfaces 1. Fundamentals and Application to Plane Surface Junctions. Surf. Sci. 1972, 31, 368–388. [Google Scholar] [CrossRef]
- Rey, A.D. Mechanical model for anisotropic curved interfaces with applications to surfactant-laden liquid-liquid crystal interfaces. Langmuir 2006, 22, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, F.I. Covariant description of the properties of light beam. J. Appl. Spectrosc. 1965, 2, 344–351. [Google Scholar] [CrossRef]
- Sihvola, A.H. Institution of Electrical Engineers. In Electromagnetic Mixing Formulas and Applications; Institution of Electrical Engineers: London, UK, 1999; p. xii. 284p. [Google Scholar]







| Region | Total Wave Number | h2/h0 |
|---|---|---|
| 4 | ≠1 | |
| 4 | =1 | |
| 2 | =0 | |
| 2 | =0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Rofouie, P.; Rey, A.D. Surface Anchoring Effects on the Formation of Two-Wavelength Surface Patterns in Chiral Liquid Crystals. Crystals 2019, 9, 190. https://doi.org/10.3390/cryst9040190
Wang Z, Rofouie P, Rey AD. Surface Anchoring Effects on the Formation of Two-Wavelength Surface Patterns in Chiral Liquid Crystals. Crystals. 2019; 9(4):190. https://doi.org/10.3390/cryst9040190
Chicago/Turabian StyleWang, Ziheng, Pardis Rofouie, and Alejandro D. Rey. 2019. "Surface Anchoring Effects on the Formation of Two-Wavelength Surface Patterns in Chiral Liquid Crystals" Crystals 9, no. 4: 190. https://doi.org/10.3390/cryst9040190
APA StyleWang, Z., Rofouie, P., & Rey, A. D. (2019). Surface Anchoring Effects on the Formation of Two-Wavelength Surface Patterns in Chiral Liquid Crystals. Crystals, 9(4), 190. https://doi.org/10.3390/cryst9040190