A Molecular Dynamics Study of Crosslinked Phthalonitrile Polymers: The Effect of Crosslink Density on Thermomechanical and Dielectric Properties
Abstract
:1. Introduction
2. Material and Molecular Modelling
2.1. Simulation Details
2.2. Cross-Linking Procedure
- (1)
- All activated m-APB were assumed to have the same reactivity.
- (2)
- All NH3+ reactive groups (NH2 in substitute m-APB) were assumed to have the same reactivity no matter where their position is on the crosslinked monomer.
- (3)
- A reaction will take place as long as at least one pair of reactive species are within the cutoff distance.
- (4)
- Triazines will form instantaneously at any point in the cross-linking reaction once conditions for its formation are met.
3. Results and Discussion
3.1. Thermal Properties
3.2. Mechanical Properties
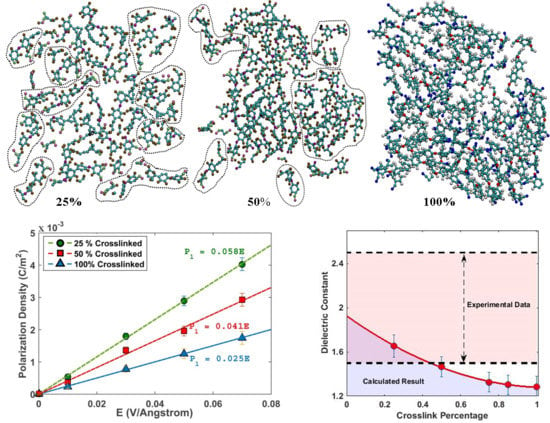
3.3. Dielectric Properties
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Keller, T.M. Imide-Containing Phthalonitrile Resin. Polymer 1993, 34, 952–955. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, M.; Roy, S.; Chu, E.K.; See, K.Y.; Hu, X. Phthalonitrile-Based Carbon Foam with High Specific Mechanical Strength and Superior Electromagnetic Interference Shielding Performance. ACS Appl. Mater. Interfaces 2016, 8, 7422–7430. [Google Scholar] [CrossRef] [PubMed]
- James, O.; Ndoke, P.N.; Kolo, S.S. Effect of Different Curing Methods on the Compressive Strength of Concrete. Available online: http://www.engineeringcivil.com/effect-of-different-curing-methods-on-the-compressive-strength-of-concrete.html (accessed on 10 March 2016).
- Kaliavaradhan, K.; Muthusamy, S. Synthesis and characterization of various phe-nylene diamine-based bismaleimide-containing phthalonitrile resins. Polym. Bull. 2016, 73, 1921–1938. [Google Scholar] [CrossRef]
- Yarovsky, I.; Evans, E. Computer simulation of structure and properties of cross-linked polymers: Application to epoxy resins. Polymer 2002, 43, 963–969. [Google Scholar] [CrossRef]
- Stevens, M.J. Manipulating connectivity to control fracture in network polymer adhe-sives. Macromolecules 2001, 34, 1411–1415. [Google Scholar] [CrossRef]
- Tsige, M.; Stevens, M.J. Effect of cross-linker functionality on the adhesion of highly cross-linked polymer networks: A molecular dynamics study of epoxies. Macromolecules 2004, 37, 630–637. [Google Scholar] [CrossRef]
- Doherty, D.C.; Holmes, B.N.; Leung, P.; Ross, R.B. Polymerization molecular dynamics simulations. I. Cross-linked atomistic models for poly(methacrylate) networks. Comput. Theor. Polym. Sci. 1998, 8, 169–178. [Google Scholar] [CrossRef]
- Wu, C.; Xu, W. Atomistic molecular modelling of crosslinked epoxy resin. Polymer 2006, 47, 6004–6009. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Valavala, P.K.; Clancy, T.C.; Wise, K.E.; Odegard, G.M. Molecular modeling of crosslinked epoxy polymers: The effect of crosslink density on thermo-mechanical properties. Polymer 2011, 52, 2445–2452. [Google Scholar] [CrossRef]
- Heine, D.R.; Grest, G.S.; Lorenz, C.D.; Tsige, M.; Stevens, M.J. Atomistic sim-ulations of end-linked poly (dimethylsiloxane) networks: Structure and relaxation. Macromolecules 2004, 37, 3857–3864. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. A molecular dynamics study of epoxy-based networks: Cross-linking procedure and prediction of molecular and material properties. Macromolecules 2008, 41, 6837–6842. [Google Scholar] [CrossRef]
- Sastri, S.B.; Keller, T.M. Phthalonitrile polymers: Cure behavior and properties. J. Polym. Sci. Part A Polym. Chem. 1999, 37, 2105–2111. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Materials Studio; Accelrys Software Inc.: San Diego, CA, USA, 2016.
- Dauber-Osguthorpe, P.; Roberts, V.A.; Osguthorpe, D.J.; Wolff, J.; Genest, M.; Hagler, A.T. Structure and energetics of ligand binding to proteins: Escherichia coli dihydrofolate reductase-trimethoprim, a drug-receptor system. Proteins Struct. Funct. Genet. 1988, 4, 31–47. [Google Scholar] [CrossRef] [PubMed]
- Burchill, P.J. On the formation and properties of a high-temperature resin from a bisphthalonitrile. J. Polym. Sci. Part A Polym. Chem. 1994, 32, 1–8. [Google Scholar] [CrossRef]
- Keller, T.M. Phthalonitrile-based conductive polymer. J. Polym. Sci. Part A Polym. Chem. 1987, 25, 2569–2576. [Google Scholar] [CrossRef]
- Itecma. High Temperature Resin PN-3M. Available online: itecma.ru/en/products/svyazuyushchie/operating-temperature-up-to-450-s/146/?type=5#downloads (accessed on 7 May 2016).
- Mulliken, A.D.; Boyce, M.C. Mechanics of the rate-dependent elastic–plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 2006, 43, 1331–1356. [Google Scholar] [CrossRef]
- Richeton, J.; Ahzi, S.; Vecchio, K.S.; Jiang, F.C.; Adharapurapu, R.R. Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers: Charac-terization and modeling of the compressive yield stress. Int. J. Solids Struct. 2006, 43, 2318–2335. [Google Scholar] [CrossRef]
- Willgert, M.; Kjell, M.H.; Jacques, E.; Behm, M.; Lindbergh, G.; Johansson, M. Photoinduced free radical polymerization of thermoset lithium battery electrolytes. Eur. Polym. J. 2011, 47, 2372–2378. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, P.; Dong, S. The Influence of Crosslink Density on the Failure Be-havior in Amorphous Polymers by Molecular Dynamics Simulations. Materials 2016, 9, 234. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Small-scale effect on the piezoelectric potential of gallium nitride nanowires. Appl. Phys. Lett. 2014, 104, 253110. [Google Scholar] [CrossRef]
- Ma, J.Z.; Cheng, K.; Lv, J.B.; Chen, C.; Hu, J.H.; Zeng, K.; Yang, G. Phthalonitrile-PPO Blends: Cure Behavior and Properties. Chin. J. Polym. Sci. 2017. [Google Scholar] [CrossRef]
- Hatton, B.D.; Landskron, K.; Hunks, W.J.; Bennett, M.R.; Shukaris, D.; Perovic, D.D.; Ozin, G.A. Materials chemistry for low-k materials. Mater. Today 2006, 9, 22–31. [Google Scholar] [CrossRef]








| CLTE | 25% | 50% | 100% |
|---|---|---|---|
| Above Tg | 15.13 | 13.70 | 12.86 |
| Below Tg | 9.99 | 8.77 | 6.99 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chua, J.; Tu, Q. A Molecular Dynamics Study of Crosslinked Phthalonitrile Polymers: The Effect of Crosslink Density on Thermomechanical and Dielectric Properties. Polymers 2018, 10, 64. https://doi.org/10.3390/polym10010064
Chua J, Tu Q. A Molecular Dynamics Study of Crosslinked Phthalonitrile Polymers: The Effect of Crosslink Density on Thermomechanical and Dielectric Properties. Polymers. 2018; 10(1):64. https://doi.org/10.3390/polym10010064
Chicago/Turabian StyleChua, Janel, and Qingsong Tu. 2018. "A Molecular Dynamics Study of Crosslinked Phthalonitrile Polymers: The Effect of Crosslink Density on Thermomechanical and Dielectric Properties" Polymers 10, no. 1: 64. https://doi.org/10.3390/polym10010064
APA StyleChua, J., & Tu, Q. (2018). A Molecular Dynamics Study of Crosslinked Phthalonitrile Polymers: The Effect of Crosslink Density on Thermomechanical and Dielectric Properties. Polymers, 10(1), 64. https://doi.org/10.3390/polym10010064