Thermal–Mechanical Coupling Behavior of Directional Polymethylmethacrylate under Tension and Compression
Abstract
:1. Introduction
2. Experimental Protocol
2.1. Material and Specimens
2.2. Quasi-Static Testing Method
2.3. Dynamic Testing Method
2.4. Temperature-Control Technology
3. Experimental Results and Analysis
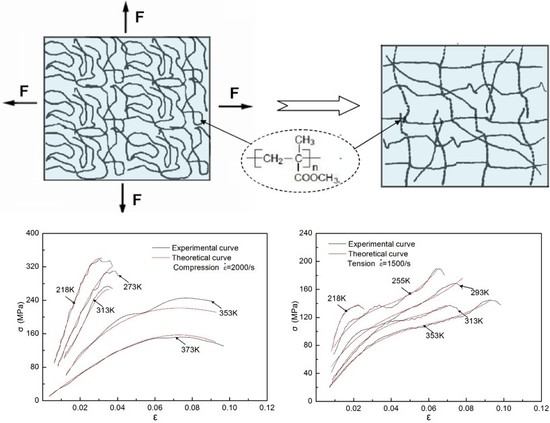
3.1. Quasi-Static and Dynamic Compressive Response at Different Temperatures
3.2. Quasi-Static and Dynamic Tensile Response at Different Temperatures
4. Constitutive Model
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Lambros, J. Strain rate effects on the thermomechanical behavior of polymers. Int. J. Solids Struct. 2001, 38, 3549–3562. [Google Scholar] [CrossRef]
- Chen, W.; Lu, F.; Cheng, M. Tension and compression tests of two polymers under quasi-static and dynamic loading. Polym. Test. 2002, 21, 113–121. [Google Scholar] [CrossRef]
- Forquin, P.; Nasraoui, M.; Rusinek, A.; Siad, L. Experimental study of the confined behavior of PMMA under quasi-static and dynamic loadings. Int. J. Impact Eng. 2012, 40–41, 46–57. [Google Scholar] [CrossRef]
- Jin, T.; Zhou, Z.; Shu, X.; Wang, Z.; Wu, G.; Liu, Z. Effects of strain rate on PMMA failure behavior. Appl. Phys. A Mater. 2016, 122, 1–7. [Google Scholar] [CrossRef]
- Jali, N.M.; Longere, P. Crack resistance of RT-PMMA under impact loading. The Eighteenth International Conference of Experimental Mechanics. Proceedings 2018, 2, 402. [Google Scholar] [CrossRef]
- Marshall, G.P.; Coutts, L.H.; Williams, J.G. Temperature effects in the fracture of PMMA. J. Mater. Sci. 1974, 9, 1409–1419. [Google Scholar] [CrossRef] [Green Version]
- Blumenthal, W.R.; Cady, C.M.; Lopez, M.F.; Gray, G.T., III; Idar, D.J. Influence of temperature and strain rate on the compressive behavior of PMMA and polycarbonate polymers. Am. Inst. Phys. 2002, 620, 665–668. [Google Scholar]
- Palm, G.; Dupaix, R.B.; Castro, J. Large strain mechanical behavior of poly (methyl methacrylate) (PMMA) near the glass transition temperature. J. Eng. Mater. Tecchnol. ASME 2006, 128, 559–563. [Google Scholar] [CrossRef]
- Abdel-Wahab, A.A.; Ataya, S.; Silberschmidt, V.V. Temperature-dependent mechanical behavior of PMMA: Experimental analysis and modeling. Polym. Test. 2017, 58, 86–95. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, L. Mechanisms of the complex thermo-mechanical behavior of polymer glass across a wide range of temperature variations. Polymers 2018, 10, 1153. [Google Scholar] [CrossRef]
- Menikoff, R. Constitutive model for polymethyl methacrylate at high pressure. J. Appl. Phys. 2004, 96, 7696–7704. [Google Scholar] [CrossRef]
- Dar, U.A.; Zhang, W.H.; Xu, Y.J. Numerical implementation of strain rate dependent thermo viscoelastic constitutive relation to simulate the mechanical behavior of PMMA. Int. J. Mech. Mater. Des. 2014, 10, 93–107. [Google Scholar] [CrossRef]
- National Technical Committee on Fiber Reinforced Plastic of Standardization Administration of China. GB/T 1448-2005 Fiber-Reinforced Plastics Composites−Determination of Compressive Properties; Standards Press of China: Beijing, China, 2005.
- Metals Handbook, Mechanical Testing and Evaluation; ASM International: Materials Park, OH, USA, 2000; Volume 8.
- Guo, H.; Guo, W.G.; Amirkhizi, A.V.; Zou, R.L.; Yuan, K. Experimental investigation and modeling of mechanical behaviors of polyurea over wide ranges of strain rates and temperatures. Polym. Test. 2016, 53, 234–244. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Zhang, B.; Forrestal, M.J. A split-Hopkinson bar technique for low impedance materials. Exp. Mech. 1999, 39, 1–5. [Google Scholar] [CrossRef]
- Wu, X.J.; Gorham, D.A. Stress equilibrium in the split Hopkinson pressure bar test. J. Phys. IV 1997, 7, C3-91–C3-96. [Google Scholar] [CrossRef]
- Pan, B.; Lu, Z.; Xie, H. Mean intensity gradient: An effective global parameter for quality assessment of the speckle patterns used in digital image correlation. Opt. Lasers Eng. 2010, 48, 469–477. [Google Scholar] [CrossRef]
- Schreier, H.W.; Braasch, J.R.; Sutton, M.A. Systematic errors in digital image correlation caused by intensity interpolation. Opt. Eng. 2000, 39, 2915–2921. [Google Scholar] [CrossRef]
- Cady, C.M.; Blumenthal, W.R.; Gray, G.T.I.; Idar, D.J. Determining the constitutive response of polymeric materials as a function of temperature and strain rate. J. Phys. IV 2003, 110, 27–32. [Google Scholar] [CrossRef]
- Guo, H.; Hu, W.; Guo, W.; Zou, R. Constitutive modeling of the viscoelastic mechanical response of foam rubber-like materials. RSC Adv. 2015, 5, 33105–33113. [Google Scholar] [CrossRef]
- Li, C.; Lua, J. A hyper-viscoelastic constitutive model for polyuria. Mater. Lett. 2009, 63, 877–880. [Google Scholar] [CrossRef]
- Hu, W.; Guo, H.; Chen, Y.; Xie, R.; Jing, H.; He, P. Experimental investigation and modeling of the rate-dependent deformation behavior of PMMA at different temperatures. Eur. Polym. J. 2016, 85, 313–323. [Google Scholar] [CrossRef]
- Rivlin, R.S. Some topics in finite elasticity. In Proceedings of First Symposium on Naval Structural Mechanics; Pergamon Press: New York, NY, USA, 1960; pp. 169–198. [Google Scholar]
- Yeoh, O.H. Some forms of strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Ogden, R.W.; Roy, P. Large Deformation isotropic elasticity on the correlation of theory and experiment for incompressible rubber like solids. Soc. Math. Phys. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Bernstein, B.; Kearsley, A.; Zapas, L.J. A study of stress relaxation with finite strain. Rubber Chem. Technol. 1965, 38, 76–89. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics, the Non-Linear Field Theories of Mechanics; Springer: Berlin/Heidelberg, Germany, 1965. [Google Scholar]
- Maurel-Pantel, A.; Baquet, E.; Bikard, J.; Bouvard, J.; Billon, N. A thermo-mechanical large deformation constitutive model for polymers based on material network description: Application to a semi-crystalline polyamide 66. Int. J. Plast. 2015, 67, 102–126. [Google Scholar] [CrossRef] [Green Version]
- Suo, T.; Li, Y.L.; Liu, Y.Y. Temperature and strain rate effects on mechanical behavior of a PMMA. Key Eng. Mater. 2007, 340–341, 1079–1084. [Google Scholar] [CrossRef]


















| C1 | C2 | C3 | C4 | C5 | C6 | A1 | A2 | |
|---|---|---|---|---|---|---|---|---|
| Compression | 264 | 302 | −2110 | 7.5 | 753 | 2.6 | 12.7 | 63.8 |
| Tension | −52.7 | 629 | 1327 | −21.4 | 106 | 4.1 | 12.7 | 63.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Lu, C.; Chen, Y.; Tao, J.; Chen, L. Thermal–Mechanical Coupling Behavior of Directional Polymethylmethacrylate under Tension and Compression. Polymers 2018, 10, 1279. https://doi.org/10.3390/polym10111279
Guo H, Lu C, Chen Y, Tao J, Chen L. Thermal–Mechanical Coupling Behavior of Directional Polymethylmethacrylate under Tension and Compression. Polymers. 2018; 10(11):1279. https://doi.org/10.3390/polym10111279
Chicago/Turabian StyleGuo, Hui, Chunjiang Lu, Yu Chen, Junlin Tao, and Longyang Chen. 2018. "Thermal–Mechanical Coupling Behavior of Directional Polymethylmethacrylate under Tension and Compression" Polymers 10, no. 11: 1279. https://doi.org/10.3390/polym10111279
APA StyleGuo, H., Lu, C., Chen, Y., Tao, J., & Chen, L. (2018). Thermal–Mechanical Coupling Behavior of Directional Polymethylmethacrylate under Tension and Compression. Polymers, 10(11), 1279. https://doi.org/10.3390/polym10111279