Coarse-Grained Simulations of Aqueous Thermoresponsive Polyethers
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Properties of The Optimized Model for Linear Ethers
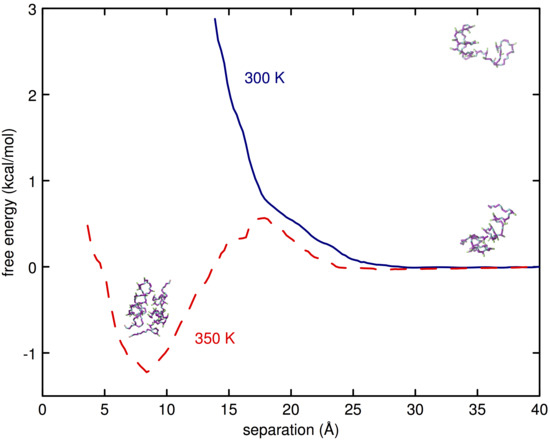
3.2. Simulations of (EO) and L42
4. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| CG | coarse-grained |
| DME | dimethoxyethane |
| EO | ethylene oxide |
| PEG | polyethylene glycol |
| PEO | polyethylene oxide |
| PO | propylene oxide |
| PPO | polypropylene oxide |
| L42 | (EO)-(PO)-(EO) |
| H | enthalpy |
| S | entropy |
| w | potential of mean force |
References
- Harris, J.M. Introduction to biotechnical and biomedical applications of poly(ethylene glycol). In Poly(Ethylene Glycol) Chemistry: Biotechnical and Biomedical Applications; Harris, J.M., Ed.; Springer: Boston, MA, USA, 1992; pp. 1–14. [Google Scholar]
- Ward, M.A.; Georgiou, T.K. Thermoresponsive polymers for biomedical applications. Polymers 2011, 3, 1215–1242. [Google Scholar] [CrossRef]
- Alexandridis, P.; Hatton, T.A. Poly(ethylene oxide)-poly(propylene oxide)-poly(ethylene oxide) block copolymer surfactants in aqueous solutions and at interfaces: Thermodynamics, structure, dynamics, and modeling. Colloids Surf. A Physicochem. Eng. Asp. 1995, 96, 1–46. [Google Scholar] [CrossRef]
- Pitto-Barry, A.; Barry, N.P.E. Pluronic block-copolymers in medicine: From chemical and biological versatility to rationalisation and clinical advances. Polym. Chem. 2014, 5, 3291–3297. [Google Scholar] [CrossRef]
- Briggs, J.M.; Matsui, T.; Jorgensen, W.L. Monte-Carlo simulations of liquid alkyl ethers with The OPLS potential functions. J. Comp. Chem. 1990, 11, 958–971. [Google Scholar] [CrossRef]
- Bedrov, D.; Pekny, M.; Smith, G.D. Quantum-chemistry-based force field for 1,2-dimethoxyethane and poly(ethylene oxide) in aqueous solution. J. Phys. Chem. B 1998, 102, 996–1001. [Google Scholar] [CrossRef]
- Smith, G.D.; Jaffe, R.L.; Yoon, D.Y. A force-field for simulations of 1,2-dimethoxyethane and poly(oxyethylene) based upon ab-initio electronic-structure calculations on model molecules. J. Phys. Chem. 1993, 97, 12752–12759. [Google Scholar] [CrossRef]
- Vorobyov, I.; Anisimov, V.M.; Greene, S.; Venable, R.M.; Moser, A.; Pastor, R.W.; MacKerell, A.D. Additive and classical drude polarizable force fields for linear and cyclic ethers. J. Chem. Theory Comp. 2007, 3, 1120–1133. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, G.; Shelley, J.C.; Nielsen, S.O.; Discher, D.E.; Klein, M.L. Simulation of diblock copolymer self-assembly, using a coarse-grain model. J. Phys. Chem. B 2004, 108, 8153–8160. [Google Scholar] [CrossRef]
- Bedrov, D.; Ayyagari, C.; Smith, G.D. Multiscale modeling of poly(ethylene oxide)-poly(propylene oxide)-poly(ethylene oxide) triblock copolymer micelles in aqueous solution. J. Chem. Theory Comput. 2006, 2, 598–606. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; de Vries, A.H.; Marrink, S.J.; Pastor, R.W. A coarse-grained model for polyethylene oxide and polyethylene glycol: Conformation and hydrodynamics. J. Phys. Chem. B 2009, 113, 13186–13194. [Google Scholar] [CrossRef] [PubMed]
- Rossi, G.; Fuchs, P.F.J.; Barnoud, J.; Monticelli, L. A coarse-grained MARTINI model of polyethylene glycol and of polyoxyethylene alkyl ether surfactants. J. Phys. Chem. B 2012, 116, 14353–14362. [Google Scholar] [CrossRef] [PubMed]
- Lee, H. Molecular modeling of PEGylated peptides, dendrimers, and single-walled carbon nanotubes for biomedical applications. Polymers 2014, 6, 776–798. [Google Scholar] [CrossRef]
- Fischer, J.; Paschek, D.; Geiger, A.; Sadowski, G. Modeling of Aqueous Poly(oxyethylene) Solutions. 2. Mesoscale Simulations. J. Phys. Chem. B 2008, 112, 13561–13571. [Google Scholar] [CrossRef] [PubMed]
- Prasitnok, K.; Wilson, M.R. A coarse-grained model for polyethylene glycol in bulk water and at a water/air interface. Phys. Chem. Chem. Phys. 2013, 15, 17093–17104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chudoba, R.; Heyda, J.; Dzubiella, J. Temperature-dependent implicit-solvent model of polyethylene glycol in aqueous solution. J. Chem. Theory Comput. 2017, 13, 6317–6327. [Google Scholar] [CrossRef] [PubMed]
- Boţan, V.; Ustach, V.; Faller, R.; Leonhard, K. Direct phase equilibrium simulations of NIPAM oligomers in water. J. Phys. Chem. B 2016, 120, 3434–3440. [Google Scholar] [CrossRef] [PubMed]
- Stillinger, F.H.; Weber, T.A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 1986, 31, 5262–5271. [Google Scholar] [CrossRef]
- Molinero, V.; Moore, E.B. Water modeled as an intermediate element between carbon and solicon. J. Phys. Chem. B 2009, 113, 4008–4016. [Google Scholar] [CrossRef] [PubMed]
- Larini, L.; Lu, L.; Voth, G.A. The multiscale coarse-graining method. VI. Implementation of three-body coarse-grained potentials. J. Chem. Phys. 2010, 132, 164107. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Andersen, H.C. The multiscale coarse-graining method. IX. A general method for construction of three body coarse-grained force field. J. Chem. Phys. 2012, 136, 194114. [Google Scholar] [CrossRef] [PubMed]
- DeMille, R.C.; Molinero, V. Coarse-grained ions without charges: Reproducing The solvation structure of NaCl in water using short-ranged potentials. J. Chem. Phys. 2009, 131, 034107. [Google Scholar] [CrossRef] [PubMed]
- Song, B.; Molinero, V. Thermodynamic and structural signatures of water-driven methane-methane attraction in coarse-grained mW water. J. Chem. Phys. 2013, 139, 054511. [Google Scholar] [PubMed]
- Gyawali, G.; Sternfield, S.; Kumar, R.; Rick, S.W. Coarse-grained models of aqueous and pure liquid alkanes. J. Chem. Theory Comput. 2017, 13, 3846–3853. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.L.; Fischer, J.T.; Chandra, A.; Brooks, B.R.; Ichiye, T. A temperature of maximum density in soft sticky dipole water. Chem. Phys. Lett. 2003, 376, 646–652. [Google Scholar] [CrossRef]
- Orsi, M. Comparative assessment of The ELBA coarse-grained model for water. Mol. Phys. 2014, 112, 1566–1576. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Dodd, L.R.; Theodorou, D.N. Atomistic Monte Carlo Simulation and Continuum Mean Field Theory of The Structure and Equation of State Properties of Alkane and Polymer Melts. Adv. Polym. Sci. 1994, 116, 249. [Google Scholar]
- Ashbaugh, H.S.; Liu, L.; Surampdi, L.N. Optimization of linear and branched alkane interactions with water to simulate hydrophobic hydration. J. Chem. Phys. 2011, 135, 054510. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, L.C.; Molinero, V. A methane-water model for coarse-grained simulations of solutions and clathrate hydrates. J. Phys. Chem. B 2010, 114, 7302–7311. [Google Scholar] [CrossRef] [PubMed]
- Stubbs, J.M.; Potoff, J.J.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 6. United-Atom Description for Ethers, Glycols, Ketones, and Aldehydes. J. Phys. Chem. 2004, 108, 17596–17605. [Google Scholar] [CrossRef]
- Faller, R.; Schmitz, H.; Biermann, O.; Müller-Plathe, F. Automatic parameterization of force fields for liquids by simplex optimization. J. Comput. Chem. 1999, 20, 1009–1017. [Google Scholar] [CrossRef]
- Wang, L.P.; Martinez, T.J.; Pande, V.S. Building force fields: An automatic, systematic, and reproducible approach. J. Phys. Chem. Lett. 2014, 5, 1885–1891. [Google Scholar] [CrossRef] [PubMed]
- Mezei, M. The finite difference thermodynamic integration, tested on calculating The hydration free energy difference between acetone and dimethylamine in water. J. Chem. Phys. 1987, 86, 7084–7088. [Google Scholar] [CrossRef]
- Beutler, T.C.; Mark, A.E.; van Schaik, R.C.; Gerber, P.R.; van Gunsteren, W.F. Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett. 1994, 222, 529–539. [Google Scholar] [CrossRef]
- A Git Repository for the Free Energy Routines Is Hosted. Available online: https://github.com/ggyawali/pair_sw_soft/tree/master (accessed on 28 April 2017).
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible and Free. J. Comp. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of The OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269. [Google Scholar] [CrossRef]
- Das, B.; Roy, M.N.; Hazra, D.K. Densities and Viscosities of The Binary Aqueous Mixtures of Tetrahydrofuran and 1,2-Dimethoxyethane at 198, 308 and 318 K. Indian J. Chem. Technol. 1994, 1, 93–97. [Google Scholar]
- Weast, R.C. (Ed.) CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Zhao, G.J.; Bi, S.S.; Li, X.; Wu, J.T. Surface tension of diethyl carbonate, 1,2-dimethoxyethane and diethyl adipate. Fluid Phase Equilib. 2010, 295, 46–49. [Google Scholar] [CrossRef]
- Fischer, J.; Paschek, D.; Geiger, A.; Sadowski, G. Modeling of Aqueous Poly(oxyethylene) Solutions. 1. Atomistic Simulations. J. Phys. Chem. B 2008, 112, 2388–2398. [Google Scholar] [CrossRef] [PubMed]
- Cabani, S.; Gianni, P.; Mollica, V.; Lepori, L. Group Contributions to The Thermodynamic Properties of Non-Ionic Organic Solutes in Dilute Aqueous-Solution. J. Solut. Chem. 1981, 10, 563–595. [Google Scholar] [CrossRef]
- Horn, H.W.; Swope, W.C.; Pitera, J.W.; Madera, J.D.; Dick, T.J.; Hura, G.L.; Head-Gordon, T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Kawaguchi, S.; Imai, G.; Suzuki, J.; Miyahara, A.; Kitano, T. Aqueous solution properties of oligo- and poly(ethylene oxide) by static light scattering and intrinsic viscosity. Polymer 1997, 38, 2885–2891. [Google Scholar] [CrossRef]
- Devanand, K.; Selser, J.C. Asymptotic-behavior and long-range interactions in aqueous-solutions of poly(ethylene oxide). Macromolecules 1991, 24, 5943–5947. [Google Scholar] [CrossRef]
- Lee, H.; Venable, R.M.; MacKerell, A.D.; Pastor, R.W. Molecular dynamics studies of polyethylene oxide and polyethylene glycol: Hydrodynamic radius and shape anisotropy. Biophys. J. 2008, 95, 1590–1599. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.D.; Bedrov, D.; Borodin, O. Molecular Dynamics Simulation Study of Hydrogen Bonding in Aqueous Poly(Ethylene Oxide) Solutions. Phys. Rev. Lett. 2000, 85, 5583–5586. [Google Scholar] [CrossRef] [PubMed]
- Abbott, N.L.; Blankschtein, D.; Hatton, T.A. Protein partitioning in two-phase aqueous polymer systems. 3. A neutron scattering investigation of The polymer solution structure and protein-polymer interactions. Macromolecules 1992, 25, 3932–3941. [Google Scholar] [CrossRef]
- Thiyagarajan, P.; Chaiko, D.J.; Hjelm, R.P. A neutron xcattering study of poly(ethylene glycol) in electrolyte solutions. Macromolecules 1995, 28, 7730–7736. [Google Scholar] [CrossRef]
- Kjellander, R.; Florin, E. Water structure and changes in thermal stability of The system poly(ethylene oxide)-water. J. Chem. Soc. Faraday Trans. 1981, 77, 2053–2077. [Google Scholar] [CrossRef]
- Karlström, G. A New Model for Upper and Lower Critical Solution Temperatures in Poly(ethy1ene oxide) Solutions. J. Phys. Chem. 1985, 89, 4962–4964. [Google Scholar] [CrossRef]
- Dormidontova, E.E. Role of Competitive PEO-Water and Water-Water Hydrogen Bonding in Aqueous Solution PEO Behavior. Macromolecules 2002, 35, 987–1001. [Google Scholar] [CrossRef]
- Smith, G.D.; Bedrov, D. Roles of Enthalpy, Entropy, and Hydrogen Bonding in The Lower Critical Solution Temperature Behavior of Poly(ethylene oxide)/Water Solutions. J. Phys. Chem. B 2003, 107, 3095–3097. [Google Scholar] [CrossRef]
- Ashbaugh, H.S.; Paulaitis, M.E. Monomer Hydrophobicity as a Mechanism for The LCST Behavior of Poly(ethylene oxide) in Water. Ind. Eng. Chem. Res. 2006, 45, 5531–5537. [Google Scholar] [CrossRef]
- Ho, B.H.D.L.; Kline, S. Insight into Clustering in Poly(ethylene oxide) Solutions. Macromolecules 2004, 37, 6932–6937. [Google Scholar]













| (Å) | (kcal/mol) | a (Å) | ||
|---|---|---|---|---|
| CH | CH | 3.98 | 0.11 | 1.8 |
| CH | CH | 3.98 | 0.11 | 1.8 |
| CH | CH | 3.98 | 0.11 | 1.8 |
| CH | O | 3.14 | 0.40 | 2.0 |
| CH | O | 3.14 | 0.40 | 2.0 |
| O | O | 4.10 | 0.10 | 1.8 |
| CH | HO | 3.65 | 0.44 | 1.8 |
| CH | HO | 3.54 | 0.44 | 1.8 |
| O | HO | 2.20 | 4.20 | 1.8 |
| CH (A) | CH (A) | 4.64 | 0.100 | 1.8 |
| CH (A) | HO | 4.25 | 0.165 | 1.8 |
| HO | HO | 2.3925 | 6.189 | 1.8 |
| (kcal/mol) | cos () | ||||
|---|---|---|---|---|---|
| CH | CH | O | 0.10 | 4.55 | 0.64 |
| CH | CH | O | 0.10 | 4.55 | 0.64 |
| CH | CH | O | 0.10 | 4.55 | 0.64 |
| CH | CH | O | 0.10 | 4.55 | 0.64 |
| CH | O | O | 0.40 | 1.8 | 0.07 |
| CH | O | O | 0.40 | 1.8 | 0.07 |
| O | CH | CH | 0.40 | 1.8 | 0.17 |
| O | CH | CH | 0.40 | 1.8 | 0.17 |
| O | CH | CH | 0.40 | 1.8 | 0.17 |
| O | CH | CH | 0.40 | 1.8 | 0.17 |
| O | CH | O | 0.10 | 4.55 | 0.68 |
| O | CH | O | 0.10 | 4.55 | 0.68 |
| O | O | HO | 3.50 | 10.0 | 0.14 |
| O | HO | HO | 4.20 | 18.5 | −1/2 |
| HO | CH | CH | 0.44 | 10.0 | −1/2 |
| HO | CH | CH | 0.44 | 10.0 | −1/2 |
| HO | CH | CH | 0.44 | 8.0 | −1/2 |
| HO | O | O | 4.20 | 10.0 | −1/3 |
| HO | HO | O | 6.189 | 20.0 | −1/2 |
| HO | HO | HO | 6.189 | 23.15 | −1/3 |
| Model | Experiment | |
|---|---|---|
| density (g/cm) | 0.864 ± 0.002 | 0.861 |
| H (kcal/mol) | 8.2 ± 0.2 | 8.79 |
| surface tension (nm/m) | 26 ± 2 | 23.9 |
| G (kcal/mol) | −6.4 ± 0.1 | −4.8 |
| H (kcal/mol) | −13.5 ± 0.6 | −14.2 |
| S (cal/(mol K)) | −24 ± 2 | −31.5 |
| CH–CH | CH–O | O–O | ||
|---|---|---|---|---|
| Intra-Chain | Inter-Chain | |||
| contact pair | 41 ± 1 | 14 ± 1 | 286 ± 4 | 39 ± 1 |
| separated pair | 42 ± 1 | 0 | 363 ± 3 | 46 ± 1 |
| difference | −1 ± 1 | 14 ± 1 | −77 ± 5 | −7 ± 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raubenolt, B.; Gyawali, G.; Tang, W.; Wong, K.S.; Rick, S.W. Coarse-Grained Simulations of Aqueous Thermoresponsive Polyethers. Polymers 2018, 10, 475. https://doi.org/10.3390/polym10050475
Raubenolt B, Gyawali G, Tang W, Wong KS, Rick SW. Coarse-Grained Simulations of Aqueous Thermoresponsive Polyethers. Polymers. 2018; 10(5):475. https://doi.org/10.3390/polym10050475
Chicago/Turabian StyleRaubenolt, Bryan, Gaurav Gyawali, Wenwen Tang, Katy S. Wong, and Steven W. Rick. 2018. "Coarse-Grained Simulations of Aqueous Thermoresponsive Polyethers" Polymers 10, no. 5: 475. https://doi.org/10.3390/polym10050475
APA StyleRaubenolt, B., Gyawali, G., Tang, W., Wong, K. S., & Rick, S. W. (2018). Coarse-Grained Simulations of Aqueous Thermoresponsive Polyethers. Polymers, 10(5), 475. https://doi.org/10.3390/polym10050475