Interfacial Properties and Hopping Diffusion of Small Nanoparticle in Polymer/Nanoparticle Composite with Attractive Interaction on Side Group
Abstract
:1. Introduction
2. Materials and Simulation Methods
3. Results and Discussion
3.1. Interfacial Structure and Dynamics
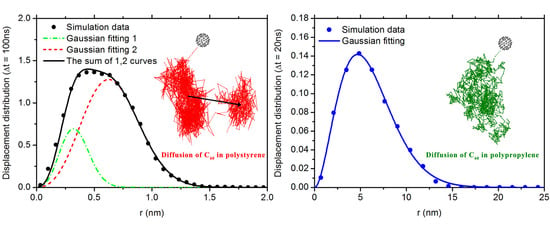
3.2. Diffusion Dynamics of C NP
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thompson, R.B.; Ginzburg, V.V.; Matsen, M.W.; Balazs, A.C. Predicting the mesophases of copolymer-nanoparticle composites. Science 2001, 292, 2469–2472. [Google Scholar] [CrossRef] [PubMed]
- Mackay, M.E.; Tuteja, A.; Duxbury, P.M.; Hawker, C.J.; Van Horn, B.; Guan, Z.; Chen, G.; Krishnan, R. General strategies for nanoparticle dispersion. Science 2006, 311, 1740–1743. [Google Scholar] [CrossRef] [PubMed]
- Warren, S.C.; DiSalvo, F.J.; Wiesner, U. Nanoparticle-tuned assembly and disassembly of mesostructured silica hybrids. Nat. Mater. 2007, 6, 156. [Google Scholar] [CrossRef] [PubMed]
- Hattemer, G.D.; Arya, G. Viscoelastic properties of polymer-grafted nanoparticle composites from molecular dynamics simulations. Macromolecules 2015, 48, 1240–1255. [Google Scholar] [CrossRef]
- Tan, H.; Xu, D.; Wan, D.; Wang, Y.; Wang, L.; Zheng, J.; Liu, F.; Ma, L.; Tang, T. Melt viscosity behavior of C60 containing star polystyrene composites. Soft Matter 2013, 9, 6282–6290. [Google Scholar] [CrossRef]
- Zia, T.U.H.; Khan, A.N.; Hussain, M.; Hassan, I.; Gul, I.H. Enhancing dielectric and mechanical behaviors of hybrid polymer nanocomposites based on polystyrene, polyaniline and carbon nanotubes coated with polyaniline. Chin. J. Polym. Sci. 2016, 34, 1500–1509. [Google Scholar] [CrossRef]
- Meesorn, W.; Shirole, A.; Vanhecke, D.; de Espinosa, L.M.; Weder, C. A simple and versatile strategy to improve the mechanical properties of polymer nanocomposites with cellulose nanocrystals. Macromolecules 2017, 50, 2364–2374. [Google Scholar] [CrossRef]
- Kropka, J.M.; Garcia Sakai, V.; Green, P.F. Local Polymer Dynamics in Polymer- C60 Mixtures. Nano Lett. 2008, 8, 1061–1065. [Google Scholar] [CrossRef] [PubMed]
- Wong, H.C.; Sanz, A.; Douglas, J.F.; Cabral, J.T. Glass formation and stability of polystyrene–fullerene nanocomposites. J. Mol. Liq. 2010, 153, 79–87. [Google Scholar] [CrossRef]
- Sanz, A.; Wong, H.C.; Nedoma, A.J.; Douglas, J.F.; Cabral, J.T. Influence of C60 fullerenes on the glass formation of polystyrene. Polymer 2015, 68, 47–56. [Google Scholar] [CrossRef]
- Kropka, J.M.; Putz, K.W.; Pryamitsyn, V.; Ganesan, V.; Green, P.F. Origin of Dynamical Properties in PMMA-C60 Nanocomposites. Macromolecules 2007, 40, 5424–5432. [Google Scholar] [CrossRef]
- Thomann, H.; Brant, P.; Dismukes, J.P.; Lohse, D.J.; Hwang, J.F.; Kresge, E.N. Fullerene-Polymer Compositions. U.S. Patent 5281653A, 25 January 1994. [Google Scholar]
- Tuteja, A.; Duxbury, P.M.; Mackay, M.E. Multifunctional nanocomposites with reduced viscosity. Macromolecules 2007, 40, 9427–9434. [Google Scholar] [CrossRef]
- Ge, T.; Kalathi, J.T.; Halverson, J.D.; Grest, G.S.; Rubinstein, M. Nanoparticle motion in entangled melts of linear and nonconcatenated ring polymers. Macromolecules 2017, 50, 1749–1754. [Google Scholar] [CrossRef] [PubMed]
- Tuteja, A.; Mackay, M.E.; Narayanan, S.; Asokan, S.; Wong, M.S. Breakdown of the continuum Stokes- Einstein relation for nanoparticle diffusion. Nano Lett. 2007, 7, 1276–1281. [Google Scholar] [CrossRef] [PubMed]
- Mackay, M.E.; Dao, T.T.; Tuteja, A.; Ho, D.L.; Van Horn, B.; Ho-Cheol, K.; Hawker, C.J. Nanoscale effects leading to non-Einstein-like decrease in viscosity. Nat. Mater. 2003, 2, 762. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, C.A.; Adhikary, B.; Mukhopadhyay, A. Dynamics of gold nanoparticles in a polymer melt. Appl. Phys. Lett. 2009, 94, 021903. [Google Scholar] [CrossRef]
- Chen, T.; Qian, H.J.; Zhu, Y.L.; Lu, Z.Y. Structure and dynamics properties at interphase region in the composite of polystyrene and cross-Linked polystyrene soft nanoparticle. Macromolecules 2015, 48, 2751–2760. [Google Scholar] [CrossRef]
- Cheng, S.; Carroll, B.; Lu, W.; Fan, F.; Carrillo, J.M.Y.; Martin, H.; Holt, A.P.; Kang, N.G.; Bocharova, V.; Mays, J.W.; et al. Interfacial Properties of Polymer Nanocomposites: Role of Chain Rigidity and Dynamic Heterogeneity Length Scale. Macromolecules 2017, 50, 2397–2406. [Google Scholar] [CrossRef]
- Cheng, S.; Holt, A.P.; Wang, H.; Fan, F.; Bocharova, V.; Martin, H.; Etampawala, T.; White, B.T.; Saito, T.; Kang, N.G.; et al. Unexpected Molecular Weight Effect in Polymer Nanocomposites. Phys. Rev. Lett. 2016, 116, 038302. [Google Scholar] [CrossRef] [PubMed]
- Ndoro, T.V.M.; Voyiatzis, E.; Ghanbari, A.; Theodorou, D.N.; Böhm, M.C.; Müller-Plathe, F. Interface of Grafted and Ungrafted Silica Nanoparticles with a Polystyrene Matrix: Atomistic Molecular Dynamics Simulations. Macromolecules 2011, 44, 2316–2327. [Google Scholar] [CrossRef]
- Ghanbari, A.; Ndoro, T.V.M.; Leroy, F.; Rahimi, M.; Böhm, M.C.; Müller-Plathe, F. Interphase Structure in Silica-Polystyrene Nanocomposites: A Coarse-Grained Molecular Dynamics Study. Macromolecules 2012, 45, 572–584. [Google Scholar] [CrossRef]
- Eslami, H.; Rahimi, M.; Müller-Plathe, F. Molecular Dynamics Simulation of a Silica Nanoparticle in Oligomeric Poly(methyl methacrylate): A Model System for Studying the Interphase Thickness in a Polymer-Nanocomposite via Different Properties. Macromolecules 2013, 46, 8680–8692. [Google Scholar] [CrossRef]
- Jouault, N.; Moll, J.F.; Meng, D.; Windsor, K.; Ramcharan, S.; Kearney, C.; Kumar, S.K. Bound Polymer Layer in Nanocomposites. ACS Macro Lett. 2013, 2, 371–374. [Google Scholar] [CrossRef]
- Jouault, N.; Crawford, M.K.; Chi, C.; Smalley, R.J.; Wood, B.; Jestin, J.; Melnichenko, Y.B.; He, L.; Guise, W.E.; Kumar, S.K. Polymer Chain Behavior in Polymer Nanocomposites with Attractive Interactions. ACS Macro Lett. 2016, 5, 523–527. [Google Scholar] [CrossRef]
- Griffin, P.J.; Bocharova, V.; Middleton, L.R.; Composto, R.J.; Clarke, N.; Schweizer, K.S.; Winey, K.I. Influence of the Bound Polymer Layer on Nanoparticle Diffusion in Polymer Melts. ACS Macro Lett. 2016, 5, 1141–1145. [Google Scholar] [CrossRef]
- Voylov, D.N.; Holt, A.P.; Doughty, B.; Bocharova, V.; Meyer, H.M.; Cheng, S.; Martin, H.; Dadmun, M.; Kisliuk, A.; Sokolov, A.P. Unraveling the Molecular Weight Dependence of Interfacial Interactions in Poly(2-vinylpyridine)/Silica Nanocomposites. ACS Macro Lett. 2017, 6, 68–72. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Theodorou, D.N. Local Segmental Dynamics and Stresses in Polystyrene–C60 Mixtures. Macromolecules 2014, 47, 387–404. [Google Scholar] [CrossRef]
- Cheng, S.; Xie, S.J.; Carrillo, J.M.Y.; Carroll, B.; Martin, H.; Cao, P.F.; Dadmun, M.D.; Sumpter, B.G.; Novikov, V.N.; Schweizer, K.S.; et al. Big Effect of Small Nanoparticles: A Shift in Paradigm for Polymer Nanocomposites. ACS Nano 2017, 11, 752–759. [Google Scholar] [CrossRef] [PubMed]
- Egorov, S.A. Anomalous nanoparticle diffusion in polymer solutions and melts: A mode-coupling theory study. J. Chem. Phys. 2011, 134, 084903. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, U.; Schweizer, K.S. Theory of nanoparticle diffusion in unentangled and entangled polymer melts. J. Chem. Phys. 2011, 135, 224902. [Google Scholar] [CrossRef] [PubMed]
- Dell, Z.E.; Schweizer, K.S. Theory of localization and activated hopping of nanoparticles in cross-linked networks and entangled polymer melts. Macromolecules 2013, 47, 405–414. [Google Scholar] [CrossRef]
- Yamamoto, U.; Schweizer, K.S. Microscopic theory of the long-time diffusivity and intermediate-time anomalous transport of a nanoparticle in polymer melts. Macromolecules 2014, 48, 152–163. [Google Scholar] [CrossRef]
- Wyart, F.B.; De Gennes, P. Viscosity at small scales in polymer melts. Eur. Phys. J. E 2000, 1, 93–97. [Google Scholar] [CrossRef]
- Cai, L.H.; Panyukov, S.; Rubinstein, M. Mobility of nonsticky nanoparticles in polymer liquids. Macromolecules 2011, 44, 7853–7863. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.H.; Panyukov, S.; Rubinstein, M. Hopping diffusion of nanoparticles in polymer matrices. Macromolecules 2015, 48, 847–862. [Google Scholar] [CrossRef] [PubMed]
- Szymański, J.; Patkowski, A.; Wilk, A.; Garstecki, P.; Holyst, R. Diffusion and viscosity in a crowded environment: From nano-to macroscale. J. Phys. Chem. B 2006, 110, 25593–25597. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Bourret, G.; Lennox, R.B.; Sutton, M.; Harden, J.L.; Leheny, R.L. Entanglement-controlled subdiffusion of nanoparticles within concentrated polymer solutions. Phys. Rev. Lett. 2012, 109, 055901. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, C.A.; Mukhopadhyay, A. Size effect of nanoparticle diffusion in a polymer melt. Macromolecules 2014, 47, 7238–7242. [Google Scholar] [CrossRef]
- Kalathi, J.T.; Grest, G.S.; Kumar, S.K. Universal viscosity behavior of polymer nanocomposites. Phys. Rev. Lett. 2012, 109, 198301. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Cao, D.; Zhang, L. Molecular dynamics study on nanoparticle diffusion in polymer melts: A test of the Stokes-Einstein law. J. Phys. Chem. C 2008, 112, 6653–6661. [Google Scholar] [CrossRef]
- Kalathi, J.T.; Yamamoto, U.; Schweizer, K.S.; Grest, G.S.; Kumar, S.K. Nanoparticle diffusion in polymer nanocomposites. Phys. Rev. Lett. 2014, 112, 108301. [Google Scholar] [CrossRef] [PubMed]
- Burgos-Mármol, J.J.; Patti, A. Unveiling the impact of nanoparticle size dispersity on the behavior of polymer nanocomposites. Polymer 2017, 113, 92–104. [Google Scholar] [CrossRef]
- Volgin, I.V.; Larin, S.V.; Abad, E.; Lyulin, S.V. Molecular dynamics simulations of fullerene diffusion in polymer melts. Macromolecules 2017, 50, 2207–2218. [Google Scholar] [CrossRef]
- Patti, A. Molecular dynamics of spherical nanoparticles in dense polymer melts. J. Phys. Chem. B 2014, 118, 3731–3742. [Google Scholar] [CrossRef] [PubMed]
- Patra, T.K.; Singh, J.K. Coarse-grain molecular dynamics simulations of nanoparticle-polymer melt: Dispersion vs. agglomeration. J. Chem. Phys. 2013, 138, 144901. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.Z.; Merlitz, H.; Wu, C.X.; Ungar, G.; Sommer, J.U. A theoretical study of dispersion-to-aggregation of nanoparticles in adsorbing polymers using molecular dynamics simulations. Nanoscale 2016, 8, 6964–6968. [Google Scholar] [CrossRef] [PubMed]
- Rossi, G.; Monticelli, L.; Puisto, S.R.; Vattulainen, I.; Ala-Nissila, T. Coarse-graining polymers with the MARTINI force-field: Polystyrene as a benchmark case. Soft Matter 2011, 7, 698–708. [Google Scholar] [CrossRef]
- Monticelli, L. On atomistic and coarse-grained models for C60 fullerene. J. Chem. Theory Comput. 2012, 8, 1370–1378. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Qian, H.J.; Carbone, P.; Chen, X.; Karimi-Varzaneh, H.A.; Liew, C.C.; Müller-Plathe, F. Temperature-transferable coarse-grained potentials for ethylbenzene, polystyrene, and their mixtures. Macromolecules 2008, 41, 9919–9929. [Google Scholar] [CrossRef]
- Sun, Q.; Faller, R. Crossover from unentangled to entangled dynamics in a systematically coarse-grained polystyrene melt. Macromolecules 2006, 39, 812–820. [Google Scholar] [CrossRef]
- Hocker, H.; Blake, G.J.; Flory, P.J. Equation-of-state parameters for polystyrene. Trans. Faraday Soc. 1971, 67, 2251–2257. [Google Scholar] [CrossRef]
- Orwoll, R.A. Physical Properties of Polymers Handbook; Mark, J.E., Ed.; American Institute of Physics: New York, NY, USA, 2007; p. 104. [Google Scholar]
- Milano, G.; Müller-Plathe, F. Mapping atomistic simulations to mesoscopic models: A systematic coarse-graining procedure for vinyl polymer chains. J. Phys. Chem. B 2005, 109, 18609–18619. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, G.R.; Windle, A.H. Structure of polystyrene glasses. Polymer 1984, 25, 906–920. [Google Scholar] [CrossRef]
- Campbell, K.; Gurun, B.; Sumpter, B.G.; Thio, Y.S.; Bucknall, D.G. Role of conformation in π–π interactions and polymer/fullerene miscibility. J. Phys. Chem. B 2011, 115, 8989–8995. [Google Scholar] [CrossRef] [PubMed]
- Flenner, E.; Das, J.; Rheinstädter, M.C.; Kosztin, I. Subdiffusion and lateral diffusion coefficient of lipid atoms and molecules in phospholipid bilayers. Phys. Rev. E 2009, 79, 011907. [Google Scholar] [CrossRef] [PubMed]
- Piskorz, T.K.; Ochab-Marcinek, A. A universal model of restricted diffusion for fluorescence correlation spectroscopy. J. Phys. Chem. B 2014, 118, 4906–4912. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Kuo, J.; Bae, S.C.; Granick, S. When Brownian diffusion is not Gaussian. Nat. Mater. 2012, 11, 481–485. [Google Scholar] [CrossRef] [PubMed]
- Szamel, G.; Flenner, E. Time scale for the onset of Fickian diffusion in supercooled liquids. Phys. Rev. E 2006, 73, 011504. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Anthony, S.M.; Bae, S.C.; Granick, S. Anomalous yet brownian. Proc. Natl. Acad. Sci. USA 2009, 106, 15160–15164. [Google Scholar] [CrossRef] [PubMed]
- Eaves, J.D.; Reichman, D.R. Spatial dimension and the dynamics of supercooled liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 15171–15175. [Google Scholar] [CrossRef] [PubMed]
- Stariolo, D.A.; Fabricius, G. Fickian crossover and length scales from two point functions in supercooled liquids. J. Chem. Phys. 2006, 125, 064505. [Google Scholar] [CrossRef] [PubMed]
- Weeks, E.R.; Crocker, J.C.; Levitt, A.C.; Schofield, A.; Weitz, D.A. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science 2000, 287, 627–631. [Google Scholar] [CrossRef] [PubMed]
- Wong, I.; Gardel, M.; Reichman, D.; Weeks, E.R.; Valentine, M.; Bausch, A.; Weitz, D. Anomalous diffusion probes microstructure dynamics of entangled F-actin networks. Phys. Rev. Lett. 2004, 92, 178101. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; He, C.; Stoykovich, M.P.; Schwartz, D.K. Nanoscale topography influences polymer surface diffusion. ACS Nano 2015, 9, 1656–1664. [Google Scholar] [CrossRef] [PubMed]
- Hurley, M.; Harrowell, P. Non-Gaussian behavior and the dynamical complexity of particle motion in a dense two-dimensional liquid. J. Chem. Phys. 1996, 105, 10521–10526. [Google Scholar] [CrossRef]
- Moreno, A.J.; Likos, C.N. Diffusion and relaxation dynamics in cluster crystals. Phys. Rev. Lett. 2007, 99, 107801. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, P.; Berthier, L.; Kob, W. Universal nature of particle displacements close to glass and jamming transitions. Phys. Rev. Lett. 2007, 99, 060604. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.; Zheng, X.; Chen, K.; Tian, Y.; Hu, G. Probing non-Gaussianity in confined diffusion of nanoparticles. J. Phys. Chem. Lett. 2016, 7, 514–519. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.; Garrahan, J.P.; Chandler, D. Dynamical exchanges in facilitated models of supercooled liquids. J. Chem. Phys. 2005, 123, 084509. [Google Scholar] [CrossRef] [PubMed]
- Hedges, L.O.; Maibaum, L.; Chandler, D.; Garrahan, J.P. Decoupling of exchange and persistence times in atomistic models of glass formers. J. Chem. Phys. 2007, 127, 211101. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D.; Garrahan, J.P. Dynamics on the Way to Forming Glass: Bubbles in Space-Time. Ann. Rev. Phys. Chem. 2010, 61, 191–217. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, E.; Akimoto, T.; Yasui, M.; Yasuoka, K. Origin of subdiffusion of water molecules on cell membrane surfaces. Sci. Rep. 2014, 4, 4720. [Google Scholar] [CrossRef] [PubMed]












| Box Size (nm) | Density (g/cm) | (nm) | (nm) | (ns) | |||
|---|---|---|---|---|---|---|---|
| PS | 5.27 | 0.952 | 40 | 20 | 0.982 ± 0.006 | 2.566 ± 0.124 | 792.03 |
| PP | 5.18 | 0.715 | 70 | 20 | 0.836 ± 0.017 | 2.041 ± 0.085 | 0.86 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, K.-X.; Jia, X.-M.; Jiao, G.-S.; Chen, T.; Qian, H.-J.; Lu, Z.-Y. Interfacial Properties and Hopping Diffusion of Small Nanoparticle in Polymer/Nanoparticle Composite with Attractive Interaction on Side Group. Polymers 2018, 10, 598. https://doi.org/10.3390/polym10060598
Ren K-X, Jia X-M, Jiao G-S, Chen T, Qian H-J, Lu Z-Y. Interfacial Properties and Hopping Diffusion of Small Nanoparticle in Polymer/Nanoparticle Composite with Attractive Interaction on Side Group. Polymers. 2018; 10(6):598. https://doi.org/10.3390/polym10060598
Chicago/Turabian StyleRen, Kai-Xin, Xiang-Meng Jia, Gui-Sheng Jiao, Tao Chen, Hu-Jun Qian, and Zhong-Yuan Lu. 2018. "Interfacial Properties and Hopping Diffusion of Small Nanoparticle in Polymer/Nanoparticle Composite with Attractive Interaction on Side Group" Polymers 10, no. 6: 598. https://doi.org/10.3390/polym10060598
APA StyleRen, K. -X., Jia, X. -M., Jiao, G. -S., Chen, T., Qian, H. -J., & Lu, Z. -Y. (2018). Interfacial Properties and Hopping Diffusion of Small Nanoparticle in Polymer/Nanoparticle Composite with Attractive Interaction on Side Group. Polymers, 10(6), 598. https://doi.org/10.3390/polym10060598