Microflow Mechanism of Oil Displacement by Viscoelastic Hydrophobically Associating Water-Soluble Polymers in Enhanced Oil Recovery
Abstract
:1. Introduction
2. Rheological Characterization of the Flow of HAWP Solutions in Porous Media
2.1. Experimental Solutions
2.2. Core Material and Initialization
2.3. Measurement Conditions
3. Mathematical Model
3.1. Continuity Equation
3.2. Momentum Equation
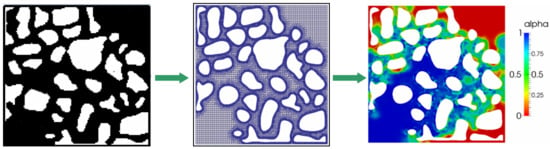
4. Physical Model
5. Numerical Simulation
5.1. Volume Fraction Characteristics
5.2. Pressure Distribution
5.3. Stress Tensor Distribution
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cai, J.; Yu, B.; Zou, M.; Mei, M. Fractal analysis of invasion depth of extraneous fluids in porous media. Chem. Eng. Sci. 2010, 65, 5178–5186. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Wang, Z.; Wang, S.; Dong, Y. The role of surface and subsurface integration in the development of a high-pressure and low-production gas field. Environ. Earth Sci. 2015, 73, 5891–5904. [Google Scholar] [CrossRef]
- Wang, Z.; Le, X.; Feng, Y.; Zhang, C. The role of matching relationship between polymer injection parameters and reservoirs in enhanced oil recovery. J. Pet. Sci. Eng. 2013, 111, 139–143. [Google Scholar] [CrossRef]
- Rui, Z.; Wang, X.; Zhang, Z.; Lu, J.; Chen, G.; Zhou, X.; Patil, S. A realistic and integrated model for evaluating oil sands development with steam assisted gravity drainage technology in Canada. Appl. Energy 2018, 213, 76–91. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, W.; Fu, J.; Lu, J.; Yin, H. The performance of polymer flooding in heterogeneous type II reservoirs–An experimental and field investigation. Energies 2017, 10, 454. [Google Scholar] [CrossRef]
- Zhang, R.; Yin, X.; Winterfeld, P.H.; Wu, Y.S. A fully coupled thermal-hydrological-mechanical-chemical model for CO2 geological sequestration. J. Nat. Gas Sci. Eng. 2016, 28, 280–304. [Google Scholar] [CrossRef]
- Wu, X.; Pu, H.; Zhu, K.; Lu, S. Formation damage mechanisms and protection technology for Nanpu nearshore tight gas reservoir. J. Pet. Sci. Eng. 2017, 158, 509–515. [Google Scholar] [CrossRef]
- Wang, D.M.; Seright, R.S.; Shao, Z.B.; Wang, J.M. Key aspects of project design for polymer flooding at the Daqing oil field. SPE Reserv. Eval. Eng. 2008, 12, 1117–1124. [Google Scholar] [CrossRef]
- Cheng, J.; Wei, J.; Song, K. Study on remaining oil distribution after polymer injection. In Proceedings of the SPE Annual Technical Conference and Exhibition SPE 133808, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Sheng, J.; Azri, N. Status of polymer-flooding technology. J. Can. Pet. Technol. 2005, 3, 116–120. [Google Scholar] [CrossRef]
- Wang, Z.H.; Liu, Y.; Pang, R.S.; Qiu, X.D. A performance evaluation of glycolipid biosurfactant synthesized by the enzyme-catalyzed method. Pet. Sci. Technol. 2005, 31, 2371–2377. [Google Scholar] [CrossRef]
- Guo, Y.; Peng, F.; Wang, H.; Huang, F.; Meng, F.; Hui, D.; Zhou, Z. Intercalation polymerization approach for preparing graphene/polymer composites. Polymers 2018, 10, 61. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, J.; Han, M.; Xiang, W.T.; Feng, G.Z.; Jiang, W.; Sun, F.J.; Zhou, S.W.; Ye, Z.B. Application of hydropholicallly associating water-soluble polymer for polymer flooding in China offshore heavy oilfield. In Proceedings of the International Petroleum Technology Conference IPTC 11635, Dubai, UAE, 4–6 December 2007. [Google Scholar]
- Liu, Y.; Wang, Z.H.; Zhuge, X.L.; Pang, R.S. Distribution of sulfide in oil-water treatment system and field test of treatment technology in Daqing oilfield. Pet. Sci. Technol. 2014, 32, 462–469. [Google Scholar] [CrossRef]
- Kang, X.D.; Zhang, J. Offshore heavy oil polymer flooding test in JZW area. In Proceedings of the SPE Heavy Oil Conference-Canada, SPE 165437, Calgary, AB, Canada, 11–13 June 2013. [Google Scholar]
- Chassenieux, C.; Nicolai, T.; Benyahia, L. Rheology of associative polymer solutions. Curr. Opin. Colloid Interface Sci. 2011, 16, 18–26. [Google Scholar] [CrossRef]
- Lu, H.; Feng, Y.; Huang, Z. Association and effective hydrodynamic thickness of hydrophobically associating polyacrylamide through porous media. J. Appl. Polym. Sci. 2008, 110, 1837–1843. [Google Scholar] [CrossRef]
- Valint, P.L., Jr.; Bock, J. Synthesis and characterization of hydrophobically associating block polymers. Macromolecules 1988, 21, 175–179. [Google Scholar] [CrossRef]
- Hill, A.; Candau, F.; Selb, J. Properties of hydrophobically associating polyacrylamides: Influence of the method of synthesis. Macromolecules 1993, 26, 4521–4532. [Google Scholar] [CrossRef]
- El-hoshoudy, A.N.; Desouky, S.E.M.; Elkady, M.Y.; Al-Sabagh, A.M.; Betiha, M.A.; Mahmoud, S. Hydrophobically associated polymers for wettability alteration and enhanced oil recovery-Article review. Egypt. J. Pet. 2017, 26, 757–762. [Google Scholar] [CrossRef]
- Samakande, A.; Hartmann, P.C.; Sanderson, R.D. Synthesis and characterization of new cationic quaternary ammonium polymerizable surfactants. J. Colloid Interface Sci. 2006, 296, 316–323. [Google Scholar] [CrossRef] [PubMed]
- Wever, D.A.Z.; Picchioni, F.; Broekhuis, A.A. Polymers for enhanced oil recovery: A paradigm for structure-property relationship in aqueous solution. Prog. Polym. Sci. 2011, 36, 1558–1628. [Google Scholar] [CrossRef]
- Alvarado, V.; Manrique, E. Enhanced oil recoverry: An update review. Energies 2010, 3, 1529–1575. [Google Scholar] [CrossRef]
- Wang, Z.H.; Liu, Y.; Le, X.P.; Yu, H.Y. The effects and control of viscosity loss of polymer solution compounded by produced water in oilfield development. Int. J. Oil Gas Coal Technol. 2014, 7, 298–307. [Google Scholar] [CrossRef]
- Carro, S.; Gonzalez-Coronel, V.J.; Castillo-Tejas, J.; Maldonado-Textle, H.; Tepale, N. Rheological properties in aqueous solution for hydrophobically modified polyacrylamides prepared in inverse emulsion polymerization. Int. J. Polym. Sci. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Candau, F.; Biggs, S.; Hill, A.; Selb, J. Synthesis, structure and properties of hydrophobically associating polymers. Prog. Org. Coatings 1994, 24, 11–19. [Google Scholar] [CrossRef]
- Nystrom, B.; Walderhaug, H.; Hansen, F.K. Dynamic crossover effects observed in solutions of a hydrophobically associating water-soluble polymer. J. Phys. Chem. 1993, 97, 7743–7752. [Google Scholar] [CrossRef]
- Taylora, K.C.; Nasr-Ei-Dinb, H.A. Water-soluble hydrophobically associating polymers for improved oil recovery: A literature review. J. Pet. Sci. Eng. 1998, 19, 265–280. [Google Scholar] [CrossRef]
- Peiffer, D.G. Hydrophobically associating polymers and their interactions with rod-like micelles. Polymer 1990, 31, 2353–2360. [Google Scholar] [CrossRef]
- Lin, Y.; Luo, K.; Huang, R. A study on P(AM-DMDA) hydrophobically associating water-soluble copolymer. Eur. Polym. J. 2000, 36, 1711–1715. [Google Scholar] [CrossRef]
- Winkler, R.G.; Elgeti, J.; Gompper, G. Active polymers-emergent conformational and dynamical properties: A brief review. J. Phys. Soc. Jpn. 2017, 86, 101014. [Google Scholar] [CrossRef]
- Wang, D.; Cheng, J.; Yang, Q.; Gong, W.; Li, Q.; Chen, F.M. Viscous-elastic polymer can increase microscale displacement efficiency in cores. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE 63227, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Xia, H.; Wang, D.; Wu, J.; Kong, F. Elasticity of HPAM solutions increases displacement efficiency under mixed wettability conditions. In Proceedings of the SPE Asia Oil and Gas Conference and Exhibition, SPE 88465, Perth, Australia, 18–20 October 2004. [Google Scholar]
- Chen, J.; Bogue, D.C. Time-dependent stress in polymer melts and review of viscoelastic theory. J. Rheol. 1972, 16, 59. [Google Scholar] [CrossRef]
- Yin, H.; Wang, D.; Zhong, H. Study on flow behaviors of viscoelastic polymer solution in micropore with dead end. In Proceedings of the SPE Annual Technical Conference and Exhibition SPE 101950, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Yin, H.; Wang, D.; Zhong, H.; Meng, S. Flow characteristics of viscoelastic polymer solution in micro-pores. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, SPE 154640, Muscat, Oman, 16–18 April 2012. [Google Scholar]
- Qi, M.; Wegner, J.; Falco, L.; Ganzer, L. Pore-scale simulation of viscoelastic polymer flow using a stabilised finite element method. In Proceedings of the SPE Reservoir Characterization and Simulation Conference and Exhibition SPE 165987, Abu Dhabi, UAE, 16–18 September 2013. [Google Scholar]
- Maerker, J.M.; Sinton, S.W. Rheology resulting from shear-induced structure in associating polymer solutions. J. Rheol. 1986, 30, 77. [Google Scholar] [CrossRef]
- Rui, Z.; Li, C.; Peng, P.; Ling, K.; Chen, G.; Zhou, X.; Chang, H. Development of industry performance metrics for offshore oil and gas project. J. Nat. Gas Sci. Eng. 2017, 39, 44–53. [Google Scholar] [CrossRef]
- Morais, A.F.; Seybold, H.; Herrmann, H.J.; Andrade, J.S. Non-newtonian fluid flow through three-dimensional disordered porous media. Phys. Rev. Lett. 2009, 103, 194502. [Google Scholar] [CrossRef] [PubMed]
- Clarke, A.; Howe, A.M.; Mitchell, J.; Staniland, J.; Hawkes, L.A. How viscoelastic-polymer flooding enhances displacement efficiency. SPE J. 2016, 21, 675–687. [Google Scholar] [CrossRef]
- Buchgraber, M.; Clemens, T.; Castanier, L.M.; Kovscek, A.R. A microvisual study of the displacement of viscous oil by polymer solutions. SPE Reserv. Eval. Eng. 2011, 14, 269–280. [Google Scholar] [CrossRef]
- Groisman, A.; Steinberg, V. Elastic turbulence in a polymer solution flow. Nature 2000, 405, 53–55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y. Exact solutions to nonlinear Schrödinger equation with variable coefficients. Appl. Math. Comput. 2011, 217, 5866–5869. [Google Scholar] [CrossRef]
- Lopez, X.; Valvatne, P.H.; Blunt, M.J. Predictive network modeling of single-phase non-Newtonian flow in porous media. J. Colloid Interface Sci. 2003, 264, 256–265. [Google Scholar] [CrossRef]















| Case | Flow Rate [m3/s] | Oil | Displacement Fluid | Interfacial Tension [mN/m] | ||||
|---|---|---|---|---|---|---|---|---|
| Density [kg/m3] | Viscosity [mPa·s] | Density [kg/m3] | Viscosity [mPa·s] | Relaxation Time [s] | ||||
| Waterflooding | 1 × 10−10 | 860 | 9 | 1000 | 1 | - | 4.8 | |
| No elastic polymer flooding | 1 × 10−10 | 860 | 9 | 900 | 12 | - | 4.8 | |
| Elastic polymer flooding (λ = 0.01) | 1 × 10−10 | 860 | 9 | 900 | ηs | ηp | 0.01 | 4.8 |
| 1 | 11 | |||||||
| Elastic polymer flooding (λ = 0.03) | 1 × 10−10 | 860 | 9 | 900 | 1 | 11 | 0.03 | 4.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, H.; Li, Y.; Zhang, W.; Yin, H.; Lu, J.; Guo, D. Microflow Mechanism of Oil Displacement by Viscoelastic Hydrophobically Associating Water-Soluble Polymers in Enhanced Oil Recovery. Polymers 2018, 10, 628. https://doi.org/10.3390/polym10060628
Zhong H, Li Y, Zhang W, Yin H, Lu J, Guo D. Microflow Mechanism of Oil Displacement by Viscoelastic Hydrophobically Associating Water-Soluble Polymers in Enhanced Oil Recovery. Polymers. 2018; 10(6):628. https://doi.org/10.3390/polym10060628
Chicago/Turabian StyleZhong, Huiying, Yuanyuan Li, Weidong Zhang, Hongjun Yin, Jun Lu, and Daizong Guo. 2018. "Microflow Mechanism of Oil Displacement by Viscoelastic Hydrophobically Associating Water-Soluble Polymers in Enhanced Oil Recovery" Polymers 10, no. 6: 628. https://doi.org/10.3390/polym10060628
APA StyleZhong, H., Li, Y., Zhang, W., Yin, H., Lu, J., & Guo, D. (2018). Microflow Mechanism of Oil Displacement by Viscoelastic Hydrophobically Associating Water-Soluble Polymers in Enhanced Oil Recovery. Polymers, 10(6), 628. https://doi.org/10.3390/polym10060628