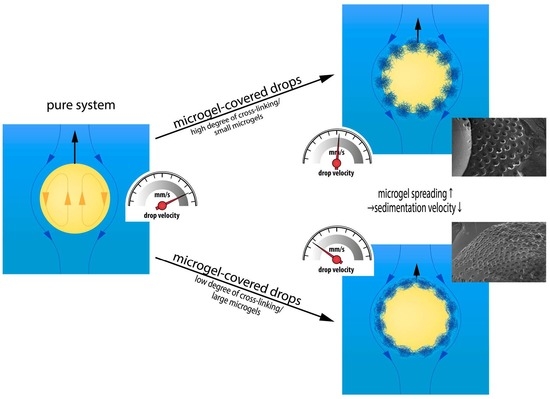
Fluid Dynamics of Microgel-Covered Drops Reveal Impact on Interfacial Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Microgels
2.3. Sedimentation Velocity Measurement
2.4. Generation of Microgel-Covered Drops
2.5. Cryo-SEM Observation
3. Results and Discussion
3.1. Sedimentation Velocity
3.2. Drag Coefficient and Deformation of Drops
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| BIS | N,N-Methylenebis(acrylamide) |
| cmc | critical micelle concentration |
| CTAB | cetyltrimethylammonium bromide |
| DLS | dynamic light scattering |
| EFCE | European Federation of Chemical Engineering |
| MG | microgel |
| SEM | scanning electron microscope |
| SF | surfactant |
| PNIPAM | Poly(N-isopropylacrylamide) |
Appendix A
| Symbol | Unit | |
|---|---|---|
| drag coefficient | - | |
| microgel concentration | /m3 | |
| drop diameter | m | |
| transition parameter | mm | |
| height of the drop path in drop generator | ||
| number of mcirogels | - | |
| hydrodynamic radius | ||
| drop velocity | /s | |
| Volume of the drop path | ||
| dimensionless numbers | ||
| We | Weber number | - |
| Re | Reynolds number | |
| greek letters | ||
| interfacial tension | N/m | |
| density of the continuous phase | / | |
| density of the disperse phase | / | |
| density difference | / |
| Component | Unit | MG1 | MG2 | MG3 | MG4 |
|---|---|---|---|---|---|
| NIPAM | 5.4008 | 4.5443 | |||
| BIS | 0.18303 | 0.3677 | 1.4708 | 0.3329 | |
| water | mL | 450 | 172 | ||
| AMPA | 0.1503 | ||||
| APMH | 0.1228 | ||||
| V50 | 0.0468 | ||||
| CTAB | 0.0058 | ||||
| reaction conditions | |||||
| stirring speed | 200 | 500 | |||
| reaction time | 2 | 3.5 | |||
| Temperature | 70 | 67 | |||
| purification | cellulose dialysis | ultracentrifugation |

References
- Pich, A.; Richtering, W. Chemical Design of Responsive Microgels; Springer: Berlin/Heidelberg, Germany, 2011; Volume 234. [Google Scholar]
- Agrawal, G.; Agrawal, R. Stimuli-Responsive Microgels and Microgel-Based Systems: Advances in the Exploitation of Microgel Colloidal Properties and Their Interfacial Activity. Polymers 2018, 10, 418. [Google Scholar] [CrossRef]
- Brugger, B.; Richtering, W. Emulsions stabilized by stimuli-sensitive poly(N-isopropylacrylamide)-co-methacrylic acid polymers: Microgels versus low molecular weight polymers. Langmuir 2008, 24, 7769–7777. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, O.S.; Maestro, A.; Duits, M.H.G.; van den Ende, D.; Stuart, M.C.; Mugele, F. Equation of state and adsorption dynamics of soft microgel particles at an air-water interface. Soft Matter 2014, 10, 7045–7050. [Google Scholar] [CrossRef] [PubMed]
- Destribats, M.; Lapeyre, V.; Sellier, E.; Leal-Calderon, F.; Schmitt, V.; Ravaine, V. Water-in-oil emulsions stabilized by water-dispersible poly(N-isopropylacrylamide) microgels: Understanding anti-Finkle behavior. Langmuir 2011, 27, 14096–14107. [Google Scholar] [CrossRef] [PubMed]
- Destribats, M.; Eyharts, M.; Lapeyre, V.; Sellier, E.; Varga, I.; Ravaine, V.; Schmitt, V. Impact of pNIPAM microgel size on its ability to stabilize Pickering emulsions. Langmuir 2014, 30, 1768–1777. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Geisel, K.; Richtering, W.; Ngai, T. Poly(N-isopropylacrylamide) microgels at the oil–water interface: Adsorption kinetics. Soft Matter 2013, 9, 9939–9946. [Google Scholar] [CrossRef]
- Wellert, S.; Richter, M.; Hellweg, T.; von Klitzing, R.; Hertle, Y. Responsive Microgels at Surfaces and Interfaces. Z. Phys. Chem. 2015, 229. [Google Scholar] [CrossRef]
- Pinaud, F.; Geisel, K.; Massé, P.; Catargi, B.; Isa, L.; Richtering, W.; Ravaine, V.; Schmitt, V. Adsorption of microgels at an oil-water interface: Correlation between packing and 2D elasticity. Soft Matter 2014, 10, 6963–6974. [Google Scholar] [CrossRef] [PubMed]
- Geisel, K.; Isa, L.; Richtering, W. Unraveling the 3D localization and deformation of responsive microgels at oil/water interfaces: A step forward in understanding soft emulsion stabilizers. Langmuir 2012, 28, 15770–15776. [Google Scholar] [CrossRef] [PubMed]
- Geisel, K.; Richtering, W.; Isa, L. Highly ordered 2D microgel arrays: Compression versus self-assembly. Soft Matter 2014, 10, 7968–7976. [Google Scholar] [CrossRef] [PubMed]
- Richtering, W. Responsive emulsions stabilized by stimuli-sensitive microgels: Emulsions with special non-Pickering properties. Langmuir 2012, 28, 17218–17229. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, S.; Liu, T.; Rütten, S.; Phan, K.H.; Möller, M.; Richtering, W. Influence of microgel architecture and oil polarity on stabilization of emulsions by stimuli-sensitive core-shell poly(N-isopropylacrylamide-co-methacrylic acid) microgels: Mickering versus Pickering behavior? Langmuir 2011, 27, 9801–9806. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wiese, S.; Balaceanu, A.; Richtering, W.; Pich, A. Behavior of Temperature-Responsive Copolymer Microgels at the Oil/Water Interface. Langmuir 2014, 30, 7660–7669. [Google Scholar] [CrossRef] [PubMed]
- Brugger, B.; Rosen, B.A.; Richtering, W. Microgels as Stimuli-Responsive Stabilizers for Emulsions. Langmuir 2008, 24, 12202–12208. [Google Scholar] [CrossRef] [PubMed]
- Destribats, M.; Lapeyre, V.; Wolfs, M.; Sellier, E.; Leal-Calderon, F.; Ravaine, V.; Schmitt, V. Soft microgels as Pickering emulsion stabilisers: Role of particle deformability. Soft Matter 2011, 7, 7689. [Google Scholar] [CrossRef]
- Bäumler, K.; Wegener, M.; Paschedag, A.R.; Bänsch, E. Drop rise velocities and fluid dynamic behavior in standard test systems for liquid/liquid extraction—Experimental and numerical investigations. Chem. Eng. Sci. 2011, 66, 426–439. [Google Scholar] [CrossRef]
- Wegener, M. A numerical parameter study on the impact of Marangoni convection on the mass transfer at buoyancy-driven single droplets. Int. J. Heat Mass Transf. 2014, 71, 769–778. [Google Scholar] [CrossRef]
- Henschke, M. Auslegung Pulsierter Siebboden-Extraktionskolonnen; Berichte aus der Verfahrenstechnik, Shaker: Aachen, Germany, 2004. [Google Scholar]
- Bertakis, E.; Groß, S.; Grande, J.; Fortmeier, O.; Reusken, A.; Pfennig, A. Validated simulation of droplet sedimentation with finite-element and level-set methods. Chem. Eng. Sci. 2010, 65, 2037–2051. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Mıšek, T.; Berger, R.; Schröter, J. Standard Test Systems for Liquid Extraction, 2nd ed.; European Federation of Chemical Engineering by Institution of Chemical Engineers: Rugby, UK, 1985. [Google Scholar]
- Wegener, M.; Eppinger, T.; Bäumler, K.; Kraume, M.; Paschedag, A.R.; Bänsch, E. Transient rise velocity and mass transfer of a single drop with interfacial instabilities—Numerical investigations. Chem. Eng. Sci. 2009, 64, 4835–4845. [Google Scholar] [CrossRef]
- Jung, Y.C.; Bhushan, B. Biomimetic structures for fluid drag reduction in laminar and turbulent flows. J. Phys. Condens. Matter 2010, 22, 035104. [Google Scholar] [CrossRef] [PubMed]
- Brauer, H.; Mewes, D. Strömungswiderstand sowie stationärer Stoff- und Wärmeübergang an Blasen und Tropfen. Chem. Ing. Tech. 1972, 44, 953–956. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. Drag Coefficients of Viscous Spheres at Intermediate and High Reynolds Numbers. J. Fluids Eng. 2001, 123, 841. [Google Scholar] [CrossRef]
- Wegener, M. Der Einfluss der Konzentrationsinduzierten Marangonikonvektion Auf Den Instationären Impuls-und Stofftransport an Einzeltropfen. Ph.D. Thesis, TU Berlin, Berlin, Germany, 2009. [Google Scholar]
- Shilin, H.; Gawlitza, K.; von Klitzing, R.; Steffen, W.; Auernhammer, G.K. Structure and Rheology of Microgel Monolayers at the Water/Oil Interface. Macromolecules 2017, 9, 3680–3689. [Google Scholar]
- Paul, N.; Schrader, P.; Enders, S.; Kraume, M. Effects of phase behaviour on mass transfer in micellar liquid/liquid systems. Chem. Eng. Sci. 2014, 115, 148–156. [Google Scholar] [CrossRef]









| Name | Cross-Linker Content | Hydrodynamic Radius |
|---|---|---|
| - | [mol %] | [nm] |
| MG1 | 2.5 | 320 |
| MG2 | 5 | 287 |
| MG3 | 20 | 310 |
| MG4 | 5 | 170 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faulde, M.; Siemes, E.; Wöll, D.; Jupke, A. Fluid Dynamics of Microgel-Covered Drops Reveal Impact on Interfacial Conditions. Polymers 2018, 10, 809. https://doi.org/10.3390/polym10080809
Faulde M, Siemes E, Wöll D, Jupke A. Fluid Dynamics of Microgel-Covered Drops Reveal Impact on Interfacial Conditions. Polymers. 2018; 10(8):809. https://doi.org/10.3390/polym10080809
Chicago/Turabian StyleFaulde, Miriam, Eric Siemes, Dominik Wöll, and Andreas Jupke. 2018. "Fluid Dynamics of Microgel-Covered Drops Reveal Impact on Interfacial Conditions" Polymers 10, no. 8: 809. https://doi.org/10.3390/polym10080809
APA StyleFaulde, M., Siemes, E., Wöll, D., & Jupke, A. (2018). Fluid Dynamics of Microgel-Covered Drops Reveal Impact on Interfacial Conditions. Polymers, 10(8), 809. https://doi.org/10.3390/polym10080809