Electrical Characteristics of Polypropylene Mixed with Natural Nanoclay
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results
3.1. Breakdown Strength
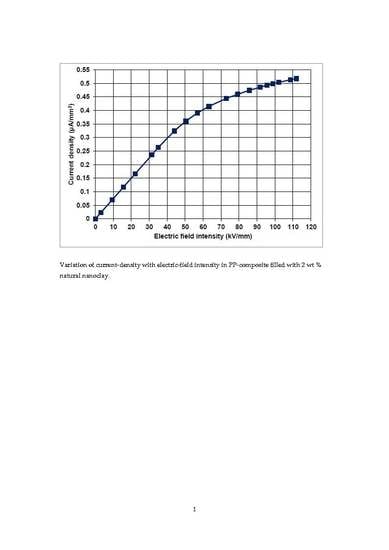
3.2. Characteristics on the Variation of Current Density as a Function of Electric-Field Intensity
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nelson, J.K. (Ed.) Background, principles and promise of nanodielectrics. In Dielectric Polymer Nanocomposites; Springer: New York, NY, USA, 2010; pp. 1–30. ISBN 978144191591-7. [Google Scholar]
- Lewis, T.J. Interfaces are the dominant feature of dielectrics at the nanometric level. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 739–753. [Google Scholar] [CrossRef]
- Pourrahimi, A.M.; Olsson, R.T.; Hedenqvist, M.S. The role of interfaces in polyethylene/metal-oxide nanocomposites for ultrahigh-voltage insulating materials. Adv. Mater. 2018, 30, 1703624. [Google Scholar] [CrossRef] [PubMed]
- Bartnikas, R.; Srivastava, K.D. Elements of Cable Engineering; Sanford Educational Press: Waterloo, ON, Canada, 1980; pp. 19–64. ISBN 0920574092. [Google Scholar]
- Nelson, J.K.; Fothergill, J.C. Internal charge behaviour of nanocomposites. Nanotechnology 2004, 15, 586–595. [Google Scholar] [CrossRef] [Green Version]
- Laihonen, S.J. Polypropylene: Morphology, Defects and Electrical Breakdown. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2005. [Google Scholar]
- Raju, G.G. Dielectrics in Electric Fields, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 183–245. ISBN 978-1-4987-6521-3. [Google Scholar]
- Moyassari, A.; Unge, M.; Hedenqvist, M.S.; Gedde, U.W.; Nilsson, F. First-principle simulations of electronic structure in semicrystalline polyethylene. J. Chem. Phys. 2017, 146, 204901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abou-Dakka, M.; Cisse, L. Evolution of some dielectric properties of polypropylene-nanoclay composites with DC poling. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Cancun, Mexico, 16–19 October 2011; pp. 628–631. [Google Scholar]
- Chung, T.C.M. Functionalization of polypropylene with high dielectric properties: Applications in Electric Energy storage. Green Sustain. Chem. 2012, 2, 29–37. [Google Scholar] [CrossRef]
- Abou-Dakka, M.; Chen, Y. Effect of Reverse Polarity on Space Charge Evolution in Polypropylene with Different Concentration of Natural and Synthetic Nano Clay. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Shenzhen, China, 20–23 October 2013; pp. 671–675. [Google Scholar]
- Andritsch, T.; Vaughan, A.; Stevens, G.C. Novel Insulation Materials for High Voltage Cable Systems Key words: Thermoplastic polymer, high voltage cable, cross-linked polyethylene. IEEE Electr. Insul. Mag. 2017, 33, 27–33. [Google Scholar] [CrossRef]
- Liu, D.; Hoang, A.T.; Pourrahimi, A.M.; Pallon, L.K.H.; Nilsson, F.; Gubanski, S.M.; Olsson, R.T.; Hedenqvist, M.S.; Gedde, U.W. Influence of nanoparticle surface coating on electrical conductivity of LDPE/Al2O3 nanocomposites for HVDC cable insulations. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1396–1404. [Google Scholar] [CrossRef]
- Liu, D.; Pallon, L.K.H.; Pourrahimi, A.M.; Zhang, P.; Diaz, A.; Holler, M.; Schneider, K.; Olsson, R.T.; Hedenqvist, M.S.; Yua, S.; et al. Cavitation in strained polyethylene/aluminium oxide nanocomposites. Eur. Polym. J. 2017, 87, 255–265. [Google Scholar] [CrossRef]
- Mammone, R.J.; Wade, W.L.; Binder, M. Extruded Films from Modified Polypropylene Resin: Dielectric and Breakdown Studies; Electronics Technology and Devices Laboratory, A Report Approved for Public Release; U.S. Army Laboratory Command: Adelphi, MD, USA, 1992. [Google Scholar]
- Cygan, P.; Krishnakumar, B.; Laghari, J.R. Lifetimes of polypropylene films under combined high electric fields and thermal stresses. IEEE Trans. Electr. Insul. 1989, 24, 619–625. [Google Scholar] [CrossRef]
- Mason, J.H. Effects of Thickness and Area on the electric Strength of Polymers. IEEE Trans. Electr. Insul. 1991, 26, 318–322. [Google Scholar] [CrossRef]
- Bulinski, A.; Bamji, S.S.; Abou-Dakka, M.; Chen, Y. Dielectric properties of polypropylene containing synthetic and natural organoclays. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, San Diego, CA, USA, 6–9 June 2010. [Google Scholar]
- Abou-Dakka, M.; Ghunem, R.A.; McIntyre, D. Space Charge Evolution in Polypropylene loaded with Synthetic and Natural Nanoclay Aged at 50 °C Temperature. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Des Moines, IA, USA, 19–22 October 2014; pp. 723–726. [Google Scholar]
- Couderc, H.; Frechette, M.; David, E. Fabrication and dielectric properties of polypropylene/silica nano-composites. In Proceedings of the IEEE Electrical Insulation Conference, Seattle, WA, USA, 7–10 June 2015; pp. 329–332. [Google Scholar]
- Hiziroglu, H.R.; Shkolnik, I.E. Electrical Breakdown of Polypropylene Filled with Natural Clay as Nanomaterial. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena, Ann Arbor, MI, USA, 18–21 October 2015; pp. 455–458. [Google Scholar]
- Utracki, L.A. Clay-containing polymeric nanocomposites and their properties. IEEE Electr. Insul. Mag. 2010, 26, 6–15. [Google Scholar] [CrossRef]
- Gómez, M.; Palza, H.; Quijada, R. Influence of organically-modified montmorillonite and synthesized layered silica nanoparticles on the properties of polypropylene and polyamide-6 nanocomposites. Polymers 2016, 8, 386. [Google Scholar] [CrossRef]
- Guru, B.S.; Hiziroglu, H.R. Electromagnetic Field Theory Fundamentals, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 94–98. ISBN 0521830168. [Google Scholar]
- Brandrup, J.; Immergut, E.H.; Grulke, E.A. Polymer Handbook, 4th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Raju, G.G. Dielectrics in Electric Fields, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; p. 79. ISBN 978-1-4987-6521-3. [Google Scholar]
- An International Collective of Scientists. Nanodielectrics: A Panacea for Solving All Electrical Insulation Problems? In Proceedings of the International Conference on Solid Dielectrics, Potsdam, Germany, 4–9 July 2010; pp. 1–29. [Google Scholar]

 90 V/s;
90 V/s;  1050 V/s.
1050 V/s.
 90 V/s;
90 V/s;  1050 V/s.
1050 V/s.






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hiziroglu, H.R.; Shkolnik, I.E. Electrical Characteristics of Polypropylene Mixed with Natural Nanoclay. Polymers 2018, 10, 942. https://doi.org/10.3390/polym10090942
Hiziroglu HR, Shkolnik IE. Electrical Characteristics of Polypropylene Mixed with Natural Nanoclay. Polymers. 2018; 10(9):942. https://doi.org/10.3390/polym10090942
Chicago/Turabian StyleHiziroglu, Huseyin R., and Iosif E. Shkolnik. 2018. "Electrical Characteristics of Polypropylene Mixed with Natural Nanoclay" Polymers 10, no. 9: 942. https://doi.org/10.3390/polym10090942
APA StyleHiziroglu, H. R., & Shkolnik, I. E. (2018). Electrical Characteristics of Polypropylene Mixed with Natural Nanoclay. Polymers, 10(9), 942. https://doi.org/10.3390/polym10090942