Role of Protein Self-Association on DNA Condensation and Nucleoid Stability in a Bacterial Cell Model
Abstract
:1. Introduction
2. Model and Systems
2.1. Model
2.2. Simulation Details
3. Results and Discussion
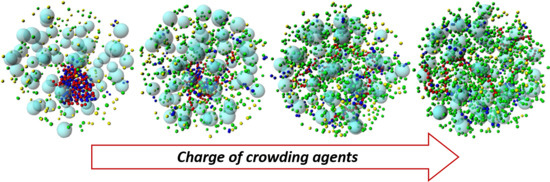
3.1. Effect of Crowding on DNA Condensation
3.2. Effect of H-NS Self-Assembly on DNA Condensation
3.3. Effect of Protein Self-Association on DNA-Protein Complex Stability
4. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Alberts, B.; Johnson, A.; Lewis, J.; Morgan, D.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 6th ed.; Garland Science: NewYork, NY, USA, 2015. [Google Scholar]
- Hacker, W.C.; Li, S.; Elcock, A.H. Features of genomic organization in a nucleotide-resolution molecular model of the Escherichia coli chromosome. Nucleic. Acid Res. 2017, 45, 7541–7554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kavenoff, R.; Ryder, O.A. Electron microscopy of membrane-associated folded chromosomes of escherichia coli. Chromosoma 1976, 55, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Tolstorukov, M.Y.; Virnik, K.; Zhurkin, V.B.; Adhya, S. Organization of DNA in a bacterial nucleoid. BMC Microbiol. 2016, 16, 22. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, S.B. Shape and compaction of Escherichia coli nucleoids. J. Stuct. Biol. 2006, 156, 255–261. [Google Scholar] [CrossRef] [PubMed]
- Asakura, S.; Oozawa, F. Interactions between particles suspended in solutions of macromolecules. J. Polym. Sci. B 1958, 33, 183–192. [Google Scholar] [CrossRef]
- Marenduzzo, D.; Finan, K.; Cook, P.R. The depletion attraction: An underappreciated force driving cellular organization. J. Cell Biol. 2006, 175, 681–686. [Google Scholar] [CrossRef] [PubMed]
- Cunha, S.; Woldringh, C.L.; Odijk, T. Polymer-Mediated Compaction and Internal Dynamics of Isolated Escherichia coli Nucleoids. J. Struct. Biol. 2001, 136, 53–66. [Google Scholar] [CrossRef] [PubMed]
- Odijk, T. Osmotic compaction of supercoiled DNA into a bacterial nucleoid. Biophys. Chem. 1998, 73, 23–29. [Google Scholar] [CrossRef]
- Zimmerman, S.B. Macromolecular crowding effects on macromolecular interactions: Some implications for genome structure and function. Biochim. Biophys. Acta 1993, 1216, 175–185. [Google Scholar] [CrossRef] [Green Version]
- Murphy, L.D.; Zimmerman, S.B. Macromolecular crowding effects on the interaction of DNA with Escherichia coli DNA-binding proteins: A model for bacterial nucleoid stabilization. Biochim. Biophys. Acta 1994, 1219, 277–284. [Google Scholar] [CrossRef]
- Murphy, L.D.; Zimmerman, S.B. Condensation and cohesion of λ DNA in cell extracts and other media: Implications for the structure and function of DNA in prokaryotes. Biophys. Chem. 1995, 57, 71–92. [Google Scholar] [CrossRef]
- de Vries, R. DNA condensation in bacteria: Interplay between macromolecular crowding and nucleoid proteins. Biochimie 2010, 92, 1715–1721. [Google Scholar] [CrossRef] [PubMed]
- Wegner, A.S.; Wintraecken, K.; Spurio, R.; Woldringh, C.L.; de Vries, R.; Odijk, T. Compaction of isolated Escherichia coli nucleoids: Polymer and H-NS protein synergetics. J. Stuct. Biol. 2016, 194, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Ramisetty, S.K.; Langlete, P.; Lale, R.; Dias, R.S. In vitro studies of DNA condensation by bridging protein in a crowding environment. Int. J. Mol. Biol. Macromol. 2017, 103, 845–853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zimmerman, S.B.; Minton, A.P. Macromolecular crowding: Biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993, 22, 27–65. [Google Scholar] [CrossRef] [PubMed]
- Dix, J.A.; Verkman, A.S. Crowding effects on diffusion in solutions and cells. Annu. Rev. Biophys. 2008, 37, 247–263. [Google Scholar] [CrossRef]
- Minton, A.P. How can biochemical reactions within cells differ from those in test tubes? J. Cell Sci. 2006, 119, 2863–2869. [Google Scholar] [CrossRef] [Green Version]
- Lerman, L.S. A Transition to a Compact Form of DNA in Polymer Solutions. Proc. Natl. Acad. Sci. USA 1971, 68, 1886–1890. [Google Scholar] [CrossRef] [Green Version]
- Bloomfield, V.A. DNA condensation. Curr. Opin. Struct. Biol. 1996, 6, 334–341. [Google Scholar] [CrossRef]
- Kojima, M.; Kubo, K.; Yoshikawa, K. Elongation/compaction of giant DNA caused by depletion interaction with a flexible polymer. J. Chem. Phys. 2006, 124, 024902. [Google Scholar] [CrossRef] [Green Version]
- Shin, J.; Cherstvy, A.G.; Metzler, R. Polymer Looping Is Controlled by Macromolecular Crowding, Spatial Confinement, and Chain Stiffness. ACS Macro Lett. 2015, 4, 202–206. [Google Scholar] [CrossRef]
- Arnold, K.; Herrmann, A.; Pratsch, L.; Gawrisch, K. The dielectric properties of aqueous solutions of poly(ethylene glycol) and their influence on membrane structure. Biochim. Biophys. Acta 1985, 815, 515–518. [Google Scholar] [CrossRef]
- Israelachvili, J. The different faces of poly(ethylene glycol). Proc. Natl. Acad. Sci. USA 1997, 94, 8378–8379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ullner, M. Polyelectrolytes. Physicochemical aspects and biological significance. In DNA Interactions with Polymers and Surfactants; Dias, R.S., Lindman, B., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Laue, T. Charge matters. Biophys. Rev. 2016, 8, 287–289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McConkey, E.H. Molecular evolution, intracellular organization, and the quinary structure of proteins. Proc. Natl. Acad. Sci. USA 1982, 79, 3236–3240. [Google Scholar] [CrossRef] [PubMed]
- Gnutt, D.; Ebbinghaus, S. The macromolecular crowding effect—From in vitro into the cell. Biol. Chem. 2016, 397, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.K.; Cherstvy, A.G.; Metzler, R. Non-universal tracer diffusion in crowded media of non-inert obstacles. Phys. Chem. Chem. Phys. 2015, 17, 1847–1858. [Google Scholar] [CrossRef] [PubMed]
- Link, A.J.; Robison, K.; Church, G.M. Comparing the predicted and observed properties of proteins encoded in the genome of Escherichia coli K-12. Electrophoresis 1997, 18, 1259–1313. [Google Scholar] [CrossRef] [PubMed]
- Ishihama, Y.; Schmidt, T.; Rappsilber, J.; Mann, M.; Hartl, F.U.; Kerner, M.J.; Frishman, D. Protein abundance profiling of the Escherichia coli cytosol. BMC Genom. 2008, 9, 102. [Google Scholar] [CrossRef] [PubMed]
- Joyeux, M. In vivo compaction dynamics of bacterial DNA: A fingerprint of DNA/RNA demixing? Curr. Opin. Colloid Interface Sci. 2016, 26, 17–27. [Google Scholar] [CrossRef] [Green Version]
- Castelnovo, M.; Gelbart, W.M. Semiflexible Chain Condensation by Neutral Depleting Agents: Role of Correlations between Depletants. Macromolecules 2004, 37, 3510–3517. [Google Scholar] [CrossRef] [Green Version]
- de Vries, R. Depletion-induced instability in protein-DNA mixtures: Influence of protein charge and size. J. Chem. Phys. 2006, 125, 014905. [Google Scholar] [CrossRef] [PubMed]
- Zinchenko, A.; Tsumoto, K.; Murata, S.; Yoshikawa, K. Crowding by Anionic Nanoparticles Causes DNA Double-Strand Instability and Compaction. J. Phys. Chem. B 2014, 118, 1256–1262. [Google Scholar] [CrossRef] [PubMed]
- Suryanarayana, T.; Subramanian, A.R. Specific association of two homologous DNA-binding proteins to the native 30-S ribosomal subunits of Escherichia coli. Biochim. Biophys. Acta 1978, 520, 342–357. [Google Scholar] [CrossRef]
- Holck, A.; Kleppe, K. Affinity of protein HU for different nucleic acids. FEBS Lett. 1985, 185, 121–124. [Google Scholar] [CrossRef] [Green Version]
- Holck, A.; Lossius, I.; Aasland, R.; Haarr, L.; Kleppe, K. DNA- and RNA-binding proteins of chromatin from Escherichia coli. Biochim. Biophys. Acta 1987, 908, 188–199. [Google Scholar] [CrossRef]
- Guo, R.; Xue, H.; Huang, L. Ssh10b, a conserved thermophilic archaeal protein, binds RNA in vivo. Mol. Microbiol. 2003, 50, 1605–1615. [Google Scholar] [CrossRef] [Green Version]
- Ainalem, M.L.; Bartles, A.; Muck, J.; Dias, R.S.; Carnerup, A.M.; Zink, D.; Nylander, T. DNA Compaction Induced by a Cationic Polymer or Surfactant Impact Gene Expression and DNA Degradation. PLoS ONE 2014, 9, e92692. [Google Scholar] [CrossRef]
- Luijsterburg, M.S.; White, M.F.; van Driel, R.; Dame, R.T. The Major Architects of Chromatin: Architectural Proteins in Bacteria, Archaea and Eukaryotes. CRC Crit. Rev. Biochem. Mol. Biol. 2008, 43, 393–418. [Google Scholar] [CrossRef]
- Ceci, P.; Cellai, S.; Falvo, E.; Rivetti, C.; Rossi, G.L.; Chiancone, E. DNA condensation and self-aggregation of Escherichia coli Dps are coupled phenomena related to the properties of the N-terminus. Nucleic Acid Res. 2004, 32, 5935–5944. [Google Scholar] [CrossRef] [Green Version]
- Waligora, E.A.; Ramsey, D.M.; Pryor, E.E.; Lu, H.; Hollis, T.; Sloan, G.P.; Deora, R.; Wozniak, D.J. AmrZ Beta-Sheet Residues Are Essential for DNA Binding and Transcriptional Control of Pseudomonas aeruginosa Virulence Genes. J. Bacteriol. 2010, 192, 5390–5401. [Google Scholar] [CrossRef] [PubMed]
- Cosgriff, S.; Chintakayala, K.; Chim, Y.T.A.; Chen, X.; Allen, S.; Lovering, A.L.; Grainger, D.C. Dimerization and DNA-dependent aggregation of the Escherichia coli nucleoid protein and chaperone CbpA. Mol. Microbiol. 2010, 77, 1289–1300. [Google Scholar] [CrossRef] [PubMed]
- Funnell, B.E. ParB Partition Proteins: Complex Formation and Spreading at Bacterial and Plasmid Centromeres. Front. Mol. Biosci. 2016, 3, 44. [Google Scholar] [CrossRef] [PubMed]
- Arold, S.T.; Leonard, P.G.; Parkinson, G.N.; Ladbury, J.E. H-NS forms a superhelical protein scaffold for DNA condensation. Proc. Natl. Acad. Sci. USA 2010, 107, 15728–15732. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hommais, F.; Krin, E.; Laurent-Winter, C.; Soutourina, O.; Malpertuy, A.; Caer, J.P.L.; Danchin, A.; Bertin, P. Large-scale monitoring of pleiotropic regulation of gene expression by the prokaryotic nucleiod-associated protein, H-NS. Mol. Microbiol. 2001, 40, 20–36. [Google Scholar] [CrossRef] [PubMed]
- Kawula, T.H.; Orndorff, P.E. Rapid Site-Specific DNA Inversion in Escherichia coli Mutants Lacking the Histone-like Protein H-NS. J. Bacteriol. 1991, 173, 4116–4123. [Google Scholar] [CrossRef] [PubMed]
- Yamada, H.; Yoshida, T.; Tanaka, K.; Sasakawa, C.; Mizuno, T. Molecular analysis of the Escherichia coli has gene encoding a DNA-binding protein, which preferentially recognizes curved DNA sequences. Mol. Gen. Genet. 1991, 230, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Dame, R.T.; Wyman, C.; Goosen, N. H-NS mediated compaction of DNA visualised by atomic force microscopy. Nucleic. Acid Res. 2000, 28, 3504–3510. [Google Scholar] [CrossRef]
- Amit, R.; Oppenheim, A.B.; Stavans, J. Increased Bending Rigidity of Single DNA Molecules by H-NS, a Temperature and Osmolarity Sensor. Biophys. J. 2003, 84, 2467–2473. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, H.; Kenney, L.J.; Yan, J. A divalent switch drives H-NS/DNA-binding conformations between stiffening and bridging modes. Genes Dev. 2010, 24, 339–344. [Google Scholar] [CrossRef] [Green Version]
- Spurio, R.; Falconi, M.; Brandi, A.; Pon, C.L.; Gualerzi, C.O. The oligomeric structure of nucleoid protein H-NS is necessary for recognition of intrinsically curved DNA and for DNA bending. EMBO J. 1997, 16, 1795–1805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rimsky, S.; Zuber, F.; Buckle, M.; Buc, H. A molecular mechanism for the repression of transcription by the H-NS protein. Mol. Microbiol. 2001, 42, 1311–1323. [Google Scholar] [CrossRef] [PubMed]
- Giangrossi, M.; Wintraecken, K.; Spurio, R.; de Vries, R. Probing the relation between protein–protein interactions and DNA binding for a linker mutant of the bacterial nucleoid protein H-NS. Biochim. Biophys. Acta 2014, 1844, 339–345. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids; Clarendon: Oxford, UK, 1987. [Google Scholar]
- Rescic, J.; Linse, P. MOLSIM: A modular molecular simulation software. J. Comput. Chem. 2015, 36, 1259–1274. [Google Scholar]
- Ramisetty, S.K.; Dias, R.S. Synergistic role of DNA-binding protein and macromolecular crowding on DNA condensation. An experimental and theoretical approach. J. Mol. Liquid 2015, 210, 64–73. [Google Scholar] [CrossRef]
- Kim, J.; Jeon, C.; Jeong, H.; Jung, Y.; Ha, B.Y. A polymer in a crowded and confined space: Effects of crowder size and poly-dispersity. Soft Matter 2015, 11, 1877–1888. [Google Scholar] [CrossRef] [PubMed]
- Dias, R.S.; Pais, A.A.C.C.; Lindman, B.; Miguel, M.G. Modeling of DNA compaction by polycations. J. Chem. Phys. 2003, 119, 8150–8157. [Google Scholar] [CrossRef]
- Dias, R.S.; Linse, P.; Pais, A.A.C.C. Stepwise disproportionation in polyeletrolyte complexes. J. Comput. Chem. 2011, 32, 2697–2707. [Google Scholar] [CrossRef]
- de Vries, R. Influence of mobile DNA-protein-DNA bridges on DNA configurations: Coarse-grained Monte-Carlo simulations. J. Chem. Phys. 2011, 135, 125104. [Google Scholar] [CrossRef]
- Joyeux, M.; Vreede, J. A Model of H-NS Mediated Compaction of Bacterial DNA. Biophys. J. 2013, 104, 1615–1622. [Google Scholar] [CrossRef] [Green Version]
- Joyeux, M. Role of Salt Valency in the Switch of H-NS Proteins between DNA-Bridging and DNA-Stiffening Modes. Biophys. J. 2018, 114, 2317–2325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holmberg, K.; Jönsson, B.; Kronberg, B.; Lindman, B. Surfactants and Polymers in Aqueous Solution, 2nd ed.; John Wiley & Sons, Inc.: West Sussex, UK, 2003. [Google Scholar]
- Dias, R.; Mel’nikov, S.; Lindman, B.; Miguel, M.G. DNA phase behavior in the presence of oppositely charged surfactants. Langmuir 2000, 16, 9577–9583. [Google Scholar] [CrossRef]
- Ceschini, S.; Lupidi, G.; Coletta, M.; Pon, C.L.; Fioretti, E.; Angeletti, M. Multimeric self-assembly equilibria involving the histone-like protein H-NS. A thermodynamic study. J. Biol. Chem. 2000, 275, 729–734. [Google Scholar] [CrossRef] [PubMed]










| Cell radius | 100 Å |
| DNA monomer radius | 2 Å |
| DNA monomer charge | −1 |
| DNA length (in no. of monomers) | 120 |
| H-NS monomer radius | 2 Å |
| H-NS monomer charge | 1 |
| H-NS length (in no. of monomers) | 2 |
| No. of H-NS | 60 |
| Attractive potential H-NS–H-NS | 0–2 kT |
| Crowder radius | 10 Å |
| Crowder surface charge density | 0– e/nm |
| Volume fraction of crowders | 0–0.06 |
| Counterion radius | 2 Å |
| Counterion charge | 1 |
| No. positively charged counterions | 120–1020 |
| No. negatively charged counterions | 120 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
S. Dias, R. Role of Protein Self-Association on DNA Condensation and Nucleoid Stability in a Bacterial Cell Model. Polymers 2019, 11, 1102. https://doi.org/10.3390/polym11071102
S. Dias R. Role of Protein Self-Association on DNA Condensation and Nucleoid Stability in a Bacterial Cell Model. Polymers. 2019; 11(7):1102. https://doi.org/10.3390/polym11071102
Chicago/Turabian StyleS. Dias, Rita. 2019. "Role of Protein Self-Association on DNA Condensation and Nucleoid Stability in a Bacterial Cell Model" Polymers 11, no. 7: 1102. https://doi.org/10.3390/polym11071102
APA StyleS. Dias, R. (2019). Role of Protein Self-Association on DNA Condensation and Nucleoid Stability in a Bacterial Cell Model. Polymers, 11(7), 1102. https://doi.org/10.3390/polym11071102