3.1. Miscibility Analysis
It is well known that a miscible polymer blend usually has a single-phase structure and presents the average properties depending on the compositions of this blend [
43,
44]. Oppositely, the immiscibility between two polymers can lead to a series phase separation and inevitably deteriorates the mechanical performance of their blending system. Therefore, it is vital to seek a miscible system for polymer blends so as to gain desirable properties. Although it has long been known that POM is seldom miscible thermodynamically with other polymers because of its specific molecular structure and crystallinity, it still indicates partially miscibility with PLA on the basis of some publications. In this work, we intended to reconfirm this thermodynamical miscibility by means of a series of typical characterization results in
Figure 1. As seen in the phase diagram of POM/PLA blends in
Figure 1a, this blending system exhibits a series of typical cloud temperatures dependent on the blending compositions due to a phase separation occurring at the critical solution temperature. Moreover, a lower critical solution temperature (LCST) was observed at around 185 °C for the blend with a POM/PLA mass ratio of 50/50, suggesting a typical miscible behavior of POM/PLA blends [
29]. The incorporation of PLA also leads to a decreasing trend in melting temperature (
Tm) of POM as a function of the PLA content as shown in
Figure 1b, in which a similar descent trend could be observed for the
Tm of PLA as a function of the POM content. It is understandable that the miscible PLA chains may disturb the crystallization process of POM chains due to the interaction between two domains in the melt state, resulting in an imperfect crystalline form accordingly. In this case, the reduction of
Tm for a semi-crystalline POM domain is considered as an indicator for its miscibility with PLA. In addition, it is noteworthy that the LCST of POM/PLA blends is far higher than its
Tm, indicating that the blends always keep a homogeneous state due to their miscible domains at low temperature even in the melt state but have to suffer a phase separation at the temperature much higher than
Tm.
On the other hand, the variation trend in glass transition temperature (
Tg) can be taken as another indicator for a miscible polymer blending system, and only one
Tg is a vital criterion for the miscibility of polymeric components. However, there are two dependent
Tg’s observed in the POM/PLA blending system according to the DSC results shown in
Figure 1c. Pure POM and PLA exhibit the
Tg’s of −73 and 66 °C, respectively. It is noteworthy that the
Tg of POM domain presents a decreasing trend as a function of the PLA content, while the PLA domain shows an opposite trend for its
Tg. Such a shift of
Tg with a variation of weight fraction of each domain is ascribed to the occurrence of phase separation between two domains due to partial miscibility, which increases the free volume for both macromolecular chains and results in a reduction of
Tg accordingly [
29]. XRD measurement was performed to confirm the effect of miscibility on the crystallinity of POM and PLA, and the resulting XRD patterns are given in
Figure 1d. Although the XRD patterns of POM/PLA blends clearly show the diffraction peaks of each domain, there is a slight fluctuation in the 2θ value observed on the (100) and (105) reflections of the POM domain with a variation of PLA content. This phenomenon can be explained by the fact that the macromolecular entanglement between POM and PLA may disturb the crystallization of POM domain, thus leading to the formation of imperfect crystals of POM domain. In this case, the Bragg angle tends to fluctuate with a variation of the PLA content.
To further confirm the driving power of miscibility between POM and PLA, FTIR spectroscopy was performed to detect the variation of characteristic absorption bands of POM and PLA domains.
Figure 2 shows the infrared spectra of POM/PLA blends at different mass ratios, which may reflect the potential interaction between two domains. As seen in
Figure 2a, pure POM exhibits two characteristic absorption peaks at 2975 and 2918 cm
−1 to the symmetric and asymmetric stretching vibrations of C−H bond, respectively. It is interesting to note in the infrared spectra of the blends that these two characteristic bands reveal a slight and constant shift to higher wavenumber with an increase of PLA loading. On the other hand, pure PLA shows a characteristics peak at 1756 cm
−1 due to the stretching vibration of its carbonyl groups as observed in
Figure 2b. This characteristic absorption band in the infrared spectra of the blends is found to continually shift to lower wavenumber with an increase of PLA loading. Qiu et al. [
29] observed the similar interesting band shifts occurring in POM and PLA domains from their blends and they considered the possible formation of hydrogen bonding between the POM and PLA molecular chains as schematically illustrated in
Figure 2c. They thought that the intrachain dipolar interaction of POM domains was reduced because of the hydrogen bond of C−H····O=C, thus resulting in a shift to higher wavenumber for the corresponding absorption bands as supported by Lee et al. [
45]. However, considering the fact that the vibrational frequencies of both domains in the partially miscible blends are influenced to a much greater extent than the reported explanations, such band shifts are more likely ascribed to the phase-separated structures in the blends.
3.2. Mechanical Properties and Fracture Morphology
The mechanical performance of POM/PLA blends was evaluated in terms of tensile, flexural, and notched impact measurements, and the obtained data are presented in
Figure 3. Pure POM is found to show pretty high tensile and flexural strength and moduli as well as good impact toughness according to the mechanical data in
Figure 3. It has been broadly reported that POM is miscible with few of polymers due to its special chain structure, and only thermoplastic polyurethane (TPU) has been generally recognized as an impact modifier for POM by now [
46]. Nevertheless, the combination of POM and TPU brings about a serious decrease in tensile and flexural properties when gaining a good toughening effect. It is found that the blending system at the POM/PLA mass ratios of 90/10 and 80/20 exhibits a slight reduction in tensile strength and modulus as well as Izod impact strength but an improvement in flexural strength and modulus. The interface existing between the POM and PLA phases may weaken the stress transfer during the tensile and impact fracture in spite of the partial miscibility of POM with PLA. The decrement in tensile and impact performance is still limited compared to other immiscible POM-based blending systems [
29,
35]. However, there are highly negative results in tensile and impact performance when the PLA loading is higher than 30 wt %, implicating that the stress transfer effect is deteriorated significantly with an increase of additional phase. It has been reported that PLA has inherent brittleness and a high sensitivity to notched impact, which are due to its low entanglement density and high value of characteristics ratios [
18]. The decrease of impact toughness of POM/PLA blends may be due to the additive behavior resulting from the increase of interface between two phases [
35], which is related to the distribution of POM and PLA domains from the surface to the core of mechanical test bar of the blends. To understand the effect of domain distribution in the test bar, Raman spectroscopy was conducted to analyze the molecular structure and composition of material surfaces, and the resulting spectra are displayed in
Figure 4. It is observed that both pure POM and PLA exhibit a set of Raman peaks at 532, 641, and 690 cm
−1 assigned to their backbone chemical structure. Pure POM is found to show a higher Raman shifting intensity than pure PLA at the peak of 532 cm
−1 due to its hexagonal structure. Moreover, pure POM also presents a characteristic Raman shift at 989 cm
−1 associated with its unique monotonic structure. It is observed in
Figure 4 that the four Raman characteristic peaks also appear in the Raman spectra of POM/PLA blends, but their shift intensity declines with an increase of PLA loading. Furthermore, there is a significant enhancement in shift intensity of these Raman peaks, especially at 989 cm
−1 when the PLA loading is lower than 30 wt %. This phenomenon suggests that the sample surface of the blends is mainly composed of a POM-rich domain when the PLA loading is lower than 30 wt %, and however there is a transition from the POM-rich domain to the PLA-rich one on the sample surface with the PLA loading over 30 wt %. Such a transition enlarges the domain size of PLA and leads to an increase in interphase tension between the POM and PLA domains accordingly. This result is disadvantageous for the mechanical strength of POM/PLA blends. As a result, the deterioration of tensile and impact strength becomes more significant.
The morphologies of impact fracture surfaces of POM/PLA blends were further investigated by SEM, and the obtained micrographs are illustrated in
Figure 5. As noted in
Figure 5a, pure POM reveals a smooth fracture surface with small matrix deformation, indicating a typical morphology from brittle fracture. On the other hand, the blends also exhibit a uniform surface with increasingly enhanced deformation in the PLA loading range of 10–30 wt %, and there is no separated phase or clear boundary between two phases observed as seen in
Figure 5b–d. When the PLA loading is improved to 40 and 50 wt %, such a homogeneous phase structure is still maintained, followed by more serious matrix deformation. Although the interface is still hard to be distinguished between the POM and PLA phases, some wrapped spherical particles seem to appear on the fracture surface as the dispersed phase of PLA (see
Figure 5e,f). These SEM observation results confirm a homogeneous phase structure in the blends even at a high loading of PLA due to the miscibility between two polymers, and therefore the deterioration in mechanical performance of the blends is effectively depressed. In summary, it is still a valuable route to gain the biodegradability for POM/PLA blends at a low loading of PLA even if there is a limited loss in tensile and impact performance compared to non-biodegradable pure POM resin.
3.4. Crystallization Behaviors and Kinetics
POM is a typical semi-crystalline polymer with a high degree of crystallinity, and it usually forms a complex heterogeneous system composed of amorphous and crystalline phases of a different order and hierarchical crystalline structure during the crystallization process. Therefore, the crystallization behavior of POM plays an important role in its production processing such as injection molding, extrusion molding and blow molding, and directly affects the properties of molded products. For example, the mechanical performance of POM is strongly associated with the molding process, especially pronounced in injection-molded devices [
35]. On the other hand, the introduction of other polymers also influences the crystallinity and crystallization behavior of POM in most cases. In this work, considering that the industrial processing conditions strongly depend on its crystallization performance with technological importance in the processability of POM/PLA blends, it is essential to well understand the crystallization behaviors and kinetics of POM domain in its blends with PLA. The non-isothermal crystallization behaviors and kinetics of POM/PLA blends were first studied by using DSC at different cooling rates, and the obtained DSC curves are illustrated in
Figure 7. As observed in
Figure 7, pure POM display a single crystallization peak (
Tp) at 148.5 °C in its DSC thermogram with a cooling rate of 2.5 °C/min, and however the
Tp is found to shift to a lower temperature with an increase of cooling rate, followed by a significant enhancement in the peak intensity of heat flow. It is understandable that a higher cooling rate corresponds to a smaller timescale for crystallization, and therefore a higher supercooling degree is required to initiate the crystallization of POM, thus leading to a longer crystallization time for POM. Although the POM/PLA blends show a similar trend in the variation of
Tp for POM domain, the
Tp’s of the blends seem to be lower than that of pure POM and tend to decrease with an increase of PLA content at all of the cooling rates. Considering the fact that the PLA domain has much lower crystallization rate and temperature than the POM one, the molten PLA evidently disturbs the crystallization of POM domain and results in a decline of
Tp.
The development of relative degree of crystallinity as a function of temperature can be derived from these DSC diagrams by Equation (1) under the non-isothermal condition, and the resulting plots are presented in
Figure 8.
where
XT is the relative degree of crystallinity,
dHc/
dT the heat flow of DSC scan,
T an arbitrary temperature, and
T0 and
T∞ are the crystallization onset and end temperatures, respectively. All of the development plots of
XT exhibit a sigmoid mode, but the crystallization period of POM domain seems to be prolonged with the addition of PLA. The non-isothermal crystallization time (
t) can be deduced from Equation (2).
where
ϕ is the cooling rate,
T0 the onset crystallization temperature at
t = 0, and
T is the temperature at crystallization time
t. To obtain the kinetic parameters, the experimental data based on the plots of
XT as a function of
T should be converted to the relative degree of crystallinity (
Xt) as a function of time by Equation (2). In this case, a crystallization kinetic analysis was conducted to evaluate the crystallization behaviors of POM and its blends with PLA using the Jeziorny-modified Avrami model with an expression as follows [
36]:
where
Xt is the relative degree of crystallinity at time
t,
n the Avrami exponent that depends on the nucleation and growth mechanism and
Z is the growth rate constant involving both nucleation and growth rate parameters. The values
n and
Z are determined from the slope and intercept of the plot of ln[−ln(1 −
Xt)] versus ln
t in terms of Equation (4).
Figure 9 shows the plots of ln[−ln(1 −
Xt)] versus ln
t, which gives a clear relationship between ln[−ln(1 −
Xt)] and ln
t with a slope of
n and an intercept of ln
Z. However, since the Avrami equation is generally applied to isothermal crystallization, it is inappropriate for describing the non-isothermal crystallization process involving a constant change of temperature. Jeziorny et al. [
36] suggested that the crystallization rate parameter
Z could be corrected for the influence of cooling rate by Equation (5).
Nevertheless, the kinetic parameter
Zc does not keep a constant as suggested by Jeziorny et al. [
33] at different scanning rates. The half crystallization time (
t1/2) defined as the time taken to complete half of the full crystallization can be calculated by Equation (6).
Furthermore, the crystallization rate parameter (CRP) is also introduced by taking into consideration the temperature width for a crystallinity degree of 50% together with the cooling rates, and it can be determined from the slope of the plots of reciprocal
t1/2 against
ϕ, as shown in
Figure S1 (see
Supplementary Material) according to Equation (7) [
47].
Furthermore, the activation energy (Δ
Ea) of non-isothermal crystallization can be calculated by the Kissinger’s equation as expressed by Equation (8) [
48]:
where
ϕ is the cooling rate,
Tp the crystallization peak temperature,
R the gas constant, and
A is the frequent factor. As a result, the values of Δ
Ea can be determined by the slope of the plot of ln(
ϕ/
Tp2) against 1/
Tp as displayed in
Figure S2 (see
Supplementary Material). All of these kinetic parameters for the non-isothermal crystallization of pure POM and its blends with PLA are collected in
Table 1. It is important to note in
Table 1 that the faster the cooling rate, the shorter the half-time (
t1/2) required for the completion of non-isothermal crystallization for both pure POM and its blends with PLA, indicating that the crystallization process can accelerated by improving the cooling rate. The Avrami exponent is found to range from two to three for both the pure POM and its blends with PLA at any given cooling rates, and however it presents an increasing trend with an improvement of cooling rate in most cases, suggesting an increase of dimension in the crystal growth with increasing the cooling rate. On the other hand, the
t1/2 value tends to increase with the incorporation of PLA into POM, whereas the Avrami exponent seems to decrease. It is found in
Table 1 that, in most cases, the
t1/2 values of POM/PLA blends are improved with increasing the PLA content at the same cooling rate under the non-isothermal condition. Although the PLA domain is in the melt state when the crystallization of POM domain occurs, the high viscose PLA chains as alien species can act as nuclei to induce the heterogeneous nucleation of POM domain. However, there are some exceptions observed in the
t1/2 value, indicating that the PLA domain serves a dual role as a nucleating agent and an obstacle due to entanglement, thus resulting in a complicated trend. On the other hand, the crystallization rate parameter is also found to decrease as observed in
Table 1, confirming the decreasing trend on a single scale of crystallization rate for the blends. It is understandable that the crystallization temperature of PLA is far lower than that of POM. Therefore, the amorphous PLA macromolecules may disturb the non-isothermal crystallization process of POM domain in the crystallization temperature range of POM and reduces the crystallization rate of blends. Although the introduction of PLA into POM leads to a decrease of the Avrami exponent at any cooling rates, the Avrami exponents of the blends are found to tend to decrease with increasing the PLA content. This result implies that the PLA macromolecules not only can act as athermal nuclei to promote the crystal growth of POM but also can hinder the molecular motion of POM domain and reduces its crystal dimensions accordingly.
The effective energy barrier for non-isothermal crystallization process of pure POM and its blends with PLA can be determined by the values of Δ
Ea shown in
Table 1. It is noteworthy that the values of crystallization activation energy of pure POM, PLA, and their blends are negative, indicating that all of them have an initiative crystallization capability. The value of Δ
Ea is found to show a decrease in the presence of 10 wt % PLA and then increases monotonically with increasing the content of PLA. This phenomenon indicates that the small amount of PLA can reduce the energy barrier of crystallization by the heterogeneous nucleation effect and promotes the crystallization of POM domain accordingly. This makes the POM domain tend to crystallize more easily and also gains a faster growth rate for crystallization. Nevertheless, it is more difficult for POM domain to crystallize at higher contents of PLA, because the large number of PLA chains may act as obstacles to the motion and diffusion of POM macromolecules, thus depressing their crystal growth in the overall non-isothermal crystallization process.
The isothermal crystallization behaviors and kinetics of POM and its blends with PLA were also studied by DSC scans at different crystallization temperatures. The development of relative degree of crystallinity as a function of crystallization time can be obtained from the DSC scans under the isothermal condition by Equation (9):
where
Xt is the relative degree of crystallinity,
dHc/
dt the heat flow rate of DSC scans and
t is an arbitrary crystallization time.
Figure 10 shows the plots of
Xt against
t at different crystallization temperatures for the isothermal crystallization of pure POM and its blends with PLA. It can be seen in
Figure 10 that all of these curves show a similar sigmoid shape, and the crystallization time for all samples seems to shorten with a decrease of crystallization temperature. Compared to pure POM, the PLA blend containing 10 wt % PLA exhibits a faster development in the relative degree of crystallinity at the given crystallization temperatures. However, the development of relative degree of crystallinity seems to become slower when the PLA content is further improved. These results indicate that the loading of PLA significantly influences the isothermal crystallization of POM domain in the blend. The isothermal crystallization kinetics of pure POM and its blends with PLA were studied by means of the well-known Avrami equation [
37,
38], which establishes the relationship between the development of
Xt against
t by Equation (10):
where
K and
n are the Avrami crystallization rate constant and Avrami exponent, respectively. The values of
K and
n can be obtained from the slope of plot of ln[−ln(1 −
Xt)] against ln
t by the following equation:
Figure 11 shows the linear fitting plots of ln[−ln(1 −
Xt)] against ln
t for the isothermal crystallization of pure POM and its blends with PLA. The half time (
t1/2) of isothermal crystallization, defined as the time required for reaching an
Xt value of 50%, is commonly used to evaluate the crystallization rates of POM/PLA blends within different environments, and it can be calculated by Equation (12).
Moreover, as the isothermal crystallization process is assumed to be thermally activated, the crystallization rate parameter
K can be approximately described by an Arrhenius equation as follows [
49]:
where
K is a temperature-independent pre-exponential factor, Δ
Ea is the total activation energy consisting of the transport activation energy Δ
E* and the nucleation activation energy Δ
F. * in Δ
E* refers to the activation energy required to transport molecular segments across the phase boundary to the crystallization surface. Δ
F is the free energy of formation of the critical size crystal nuclei at crystallization temperature
Tc,
R the universal gas constant and
T is the absolute temperature. The values of Δ
Ea can be determined by the slope of the Arrhenius plots of ln
K/
n against l/
Tc as shown in
Figure S3 (see
Supplementary Material) using the following equation:
All of these isothermal crystallization kinetic parameters derived from the analysis of the Avrami model are also summarized in
Table 1. It is noted in
Table 1 that for pure POM and its blends with PLA the
t1/2 values all present an almost exponential increase as the crystallization temperature is improved. At the same crystallization temperature, the addition of small amounts of PLA leads to a decrease of the
t1/2 value as an indicator of improved crystallization rate. This is the evidence that the crystallization of POM domain occurs by a nucleation-controlled mechanism [
49]. However, the
t1/2 values of the blends tend to increase continually with further increasing the PLA content, suggesting that the crystallization of POM domain has been controlled by the molecular-confined mechanism [
49]. It is apparent that the serious entanglement between POM and PLA chains takes place in the melt state at a high POM loading. Accordingly, the motion of POM chains is hindered during the isothermal crystallization process, resulting in a decrease of crystallization rate.
It is also clearly observed in
Table 1 that the Avrami exponents of pure POM are in the range of 1.89–2.27, implying athermal nucleation and three-dimensional growth. However, the Avrami exponent tends to decrease in the presence of PLA in most cases, suggesting athermal nucleation and two-dimensional growth for the POM domain due to the confinement of molecular motion. These results are in good agreement with the non-isothermal crystallization data. It is necessary to discuss the effect of PLA on the activation energy (Δ
Ea) of isothermal crystallization behaviors of POM domain in the blends. As seen in
Table 1, the Δ
Ea value of the blend decreases slightly in the presence of 10 wt % PLA, and furthermore, the Δ
Ea values show a continual increase as the PLA content is further improved. Such a trend is in perfect agreement with the non-isothermal crystallization results. Normally, there are two factors determining the crystallization rate of a polymer when another polymer is introduced. On the one hand, the additive polymer can play a role of heterogeneous nucleation in the crystallization process of the host polymer in the blend thus generating a positive effect on crystallization. On the other hand, the additive polymer can hinder the motion and diffusion of host polymer chains to the surface of nucleus by chain entanglement, and therefore it constrains the crystalline growth by a confinement mechanism in the blend, which leads to a negative effect on crystallization. The non-isothermal and isothermal crystallization kinetic results confirm that the PLA domain at a low content can serve as a nucleating agent to reduce the energy barriers for the non-isothermal and isothermal crystallization of POM domain. However, at the high content of PLA, the polymeric chains from POM and PLA domains are highly entangled into each other in the melt state. It is well known that the polymer chains must overcome certain energy barriers to diffuse and attach onto the growing surface of a crystal, and therefore the presence of large amounts of PLA chains may confine the motion of POM chains and hinder their crystal growth by imposing the entanglement with the POM chains. As a result, the Δ
Ea value is improved and the crystallization rate is reduced.
The real isothermal crystallization processes for pure POM and its blends with PLA were monitored by a polarizing optical microscope, and the obtained microscopic images are shown in
Figure 12. It is clearly observed that pure POM performs a fast crystallization process at a given temperature of 145 °C and forms a number of spherulites within 60 min. Compared to pure POM, the blend containing 10% PLA is found to present a slightly slower crystallization process during the same period and show a much smaller size of spherulites due to the nucleating effect of PLA. The number of spherulites is found to increase. However, the crystallization process becomes much slower with a further increase of PLA content. On the other hand, the spherulite size of the blends at the PLA content over 10 wt % become larger than that with 10 wt % of PLA, indicating that the confinement dominates the nucleation and crystallization of POM domain at the high loadings of PLA. These results confirm the conclusions obtained from the isothermal crystallization kinetic study.
3.5. Thermal Degradation Kinetics and Lifespan Prediction
TGA is considered as a powerful tool to study the thermal degradation kinetics of polymers. TGA methodology can provide important information the degradation activation energy (Δ
Ea), reaction order (
n), and frequency factor (
A) in terms of various kinetic models, and consequently, the lifetime of polymers at various temperatures can be predicted on the basis of these kinetic parameters obtained from the relevant kinetic models [
39,
40,
50,
51,
52,
53]. The thermal degradation behavior and degradation kinetics of pure POM, PLA, and their blends were evaluated by TGA at different heating rates, and some representative TGA thermograms are illustrated in
Figure 13. The degradation kinetic data including the initial degradation temperature (
Ti) corresponding to 5 wt % weight loss and final degradation temperature (
Tf) corresponding to 5 wt % residual char left calculated at different heating rates for pure POM, PLA, and POM/PLA blends are collected in
Table 2. It is clearly observed in
Figure 13 that both pure POM and PLA exhibit a typical one-step degradation behavior at the given heat rates in the temperature ranges of 250–450 and 250–360 °C, respectively. It is interesting to note that the TGA thermograms for these two polymers shift toward a higher temperature with improving the heat rate. This result suggests that the polymer has to complete thermal decomposition in a higher temperature region due to slow heat diffusion in the faster heating process [
53]. Oppositely, in the slower heating process, i.e., at a low heating rate, the polymer can rapidly achieve an equilibrium in thermal decomposition and thus complete the thermal degradation in a lower temperature region. The characteristic temperature at the maximum weight-loss rate (
Tmax) can be adopted as an important index to indicate the thermal stability of a polymer and obtained from the DTG thermogram. It is found in
Figure 13 and
Table 2 that the
Tmax’s of pure POM and PLA were distributed in the temperature range of 359.2–399.4 and 304.2–353.6 °C at the given four heating rates, respectively, indicating that pure POM has much better thermal stability than pure PLA. There are two
Tmax’s observed in the DTG thermograms of POM/PLA blends, in which the lower characteristic temperature (
Tmax,1) is attributed to PLA domain and the higher characteristic one (
Tmax,2) is associated with the thermal degradation of POM domain. It is noteworthy that the incorporation of 10 wt % PLA results in a considerable improvement in the
Tmax’s of POM and PLA domains in the blend. This phenomenon may be ascribed to the enhancement of crystallinity for POM domain as well as the envelopment effect of PLA domain in the blends. It is accepted that the high crystallinity improves the heat resistance of POM domain, while the envelopment with POM domain effectively prevents the heat diffusion to PLA domain. However, the increment becomes less with further increasing the PLA content. As seen in the DTG thermograms of
Figure 13, both
Tmax,1 and
Tmax,2 tend to decrease with reducing the heating rate, indicating that both POM and PLA domains exhibit a poorer thermal stability on a longer time scale due to the longer heating time caused by a lower heating rate.
The thermal degradation kinetics of pure POM, PLA, and their blends were studied by means of the Kissinger’s and Flynn–Wall’s methods in this work. For the thermal decomposition reaction of a polymer, the conversion (
a) of decomposition reaction is defined as the ratio of mass loss at arbitrary time to total mass loss at complete decomposition temperature from TGA analysis and can be calculated by the following equation:
where
w0,
wt, and
wf are the initial weight, actual weight at time
t, and, final weight of the sample at the end of degradation, respectively. The thermal degradation kinetics of this polymer can be expressed by Equation (16) on the basis of the reaction rate for a basic solid-state chemical reaction [
54]:
where
α is the conversion of thermal decomposition,
k the rate constant, and
n is the apparent order of reaction. The combination of the above two expressions with the Arrhenius expression gives the following relationship, which is the basis of numerous analytical approaches to the calculation of kinetic parameters from TGA data [Equations (17) and (18)]:
The degradation temperatures of pure POM, PLA, and their blends at different conversion levels are summarized in
Table S1 (see
Supplementary Material). These data indicate that the incorporation of small amounts of PLA seems not to influence the evolution of degradation reaction of the blends, and however the high content of PLA leads to a significant decrease of degradation temperature for the blends at the same conversion. According to Kissinger’ method [
51], the peak temperatures given by the maxima of the first derivative weight-loss thermogram can be used to calculate the apparent activation energy (Δ
Ea) of thermal degradation reaction by means of the following expression:
where
β is the heating rate,
T the absolute temperature corresponding to the conversion, and
R is the gas constant. On the other hand, a new expression was developed by Flynn and Wall to calculate the thermal degradation kinetic parameters of a polymer based on the Kissinger’s equation as follows [
39]:
According to the Flynn–Wall’s method, the apparent activation energy of thermal degradation reaction for pure POM, PLA, and their blends could be obtained from the slope of the linear plot of ln
β versus 1/
T at a fixed conversion (normally taken as 5% conversion) [
39].
Figure S4 shows the Flynn–Wall plots of ln
β versus 1/
T at the 5% conversion for all the samples (see
Supplementary Material), and
Table 2 gives the apparent activation energy of thermal degradation derived from the Flynn–Wall plots. It is calculated that the apparent activation energy for the thermal degradation reactions of pure POM and PLA at a conversion of 5% is 371.8 and 309.2 kJ/mol, respectively, indicating that PLA performs thermal decomposition earlier than POM. The apparent activation energy shows a remarkable decrease with the addition of 5 wt % PLA into POM and reaches a minimum with the PLA content rising up to 20 wt %. The apparent activation energy of POM/PLA blends tends to increase continuously with a further increase of PLA content. It is well known that the apparent activation energy is associated with the initial decomposition stage [
54]. The degradation kinetic results explicitly suggest that the incorporation of small amounts of PLA can initiate the thermal degradation reaction more easily.
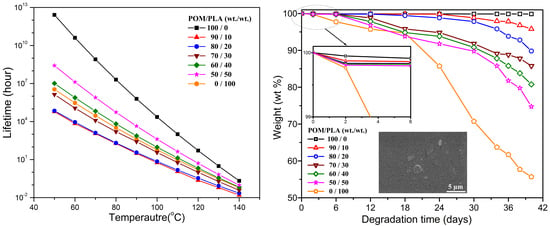
The lifespans of pure POM, PLA, and their blends in the temperature range of 50–140 °C were further predicted according to the method proposed by Toop et al. [
40] using Equations (21)–(23):
where
Xf is set as Δ
Ea/
RT5%,
T5% the absolute temperature at 5% weight loss,
Tf the failure temperature,
tf the approximate time of failure, and ln
p(
Xf) is the linear function of
Xf. The lifespans of pure POM, PLA, and their blends at different temperatures was calculated by Equation (23) on the basis of the Δ
Ea values obtained from the Flynn–Wall method, and the results of lifespan prediction are presented in
Figure 14. It is clearly observed that pure POM exhibits a much longer lifespan than pure PLA in the temperature range between 50 and 140 °C due to its structural stability. Moreover, the temperature is also found to generate a significant effect on the lifespans of these two polymers. The higher the temperature, the shorter is the lifespan as a result of the effect of thermal stability. The lifespans of POM/PLA blends are found to decrease significantly in the presence of 10 wt % PLA at all temperatures and then tends to increase with an increase of PLA content. It is noted that the lifespans of POM/PLA blends are shorter than pure PLA as long as the content of PLA is lower than 30 wt %. On the basis of the Flynn–Wall’s method and Loop’s model, the blends at the PLA contents of 10%, 20% and 30% were predicted to have the lifespans of about 6.0 × 10
4, 7.03 × 10
4, and 1.37 × 10
6 h at 50 °C, respectively. However, the lifespan of pure POM is predicted to be 2.56 × 10
12 h at 50 °C. Evidently, the introduction of 10 wt % PLA into POM can lead to the shortest lifespan in all of the POM/PLA blending samples. This percentage of PLA favors the natural degradation of the blend as well as the reservation of better mechanical performance within the lifespan of the blends.