Steps Toward the Band Gap Identification in Polystyrene Based Solid Polymer Nanocomposites Integrated with Tin Titanate Nanoparticles
Abstract
:1. Introduction
2. Experimental Details
2.1. Hybrid Fabrication
2.2. X-Ray Diffraction
2.3. UV-Vis Measurements
3. Results and Discussion
3.1. XRD Examination
3.2. Absorption Study
3.3. Absorption Edge Study
3.4. Refractive Index Analysis
3.5. Optical Dielectric Constant Study
3.6. Band Gap Study
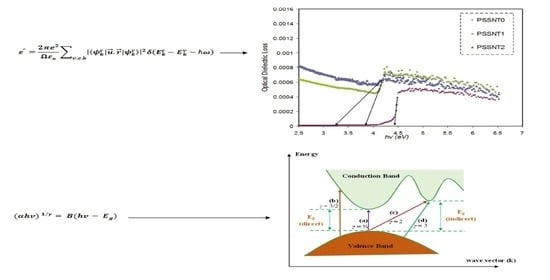
3.6.1. Optical Dielectric Loss Study
3.6.2. Tauc’s Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mohan, V.M.; Bhargav, P.B.; Raja, V.; Sharma, A.K.; NarasimhaRao, V.V.R. Optical and Electrical Properties of Pure and Doped PEO Polymer Electrolyte Films. Soft Mater. 2007, 5, 33–46. [Google Scholar] [CrossRef]
- Aziz, S.B.; Marif, R.B.; Brza, M.A.; Hassan, A.N.; Ahmad, H.A.; Faidhalla, Y.A.; Kadir, M.F.Z. Structural, thermal, morphological and optical properties of PEO filled with biosynthesized Ag nanoparticles: New insights to band gap study. Results Phys. 2019, 13, 102220. [Google Scholar] [CrossRef]
- Meyer, W.H. Polymer Electrolytes for Lithium-Ion Batteries. Adv. Mater. 1998, 10, 439–448. [Google Scholar] [CrossRef]
- Aziz, S.B.; Brza, M.A.; Mohamed, P.A.; Kadir, M.F.Z.; Hamsan, M.H.; Abdulwahid, R.T.; Woo, H.J. Increase of metallic silver nanoparticles in Chitosan: AgNt based polymer electrolytes incorporated with alumina filler. Results Phys. 2019, 13, 102326. [Google Scholar] [CrossRef]
- Ngai, K.S.; Ramesh, S.; Ramesh, K.; Juan, J.C. A review of polymer electrolytes: Fundamental, approaches and applications. Ionics 2016, 22, 1259. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y.; Liu, J.; LIu, G.; Wang, W.; Xia, Y. A PEO-based gel polymer electrolyte for lithium ion batteries. RSC Adv. 2017, 7, 23494–23501. [Google Scholar] [CrossRef] [Green Version]
- Sundaram, M.M.; Appadoo, D. Traditional salt-in-water electrolyte: Vs. water-in-salt electrolyte with binary metal oxide for symmetric supercapacitors: Capacitive vs. faradaic. Dalt. Trans. 2020, 49, 11743–11755. [Google Scholar] [CrossRef]
- Abdullah, R.M.; Aziz, S.B.; Mamand, S.M.; Hassan, A.Q.; Hussein, S.A.; Kadir, M.F.Z. Reducing the crystallite size of spherulites in PEO-based polymer nanocomposites mediated by carbon nanodots and Ag nanoparticles. Nanomaterials 2019, 9, 874. [Google Scholar] [CrossRef] [Green Version]
- Parola, S.; Julián-López, B.; Carlos, L.D.; Sanchez, C. Optical Properties of Hybrid Organic-Inorganic Materials and their Applications. Adv. Funct. Mater. 2016. [Google Scholar] [CrossRef]
- Zeranska-Chudek, K.; Lapinska, A.; Wroblewska, A.; Judek, J.; Duzynska, A.; Pawlowski, M.; Witowski, A.M.; Zdrojek, M. Study of the absorption coefficient of graphene-polymer composites. Sci. Rep. 2018, 8, 9132. [Google Scholar] [CrossRef]
- Guggillia, P.; Chilvery, A.; Powell, R. Reducing the Bandgap Energy via Doping Process in Lead-Free Thin Film Nanocomposites. Res. Rev. J. Mater. Sci. 2017, 5, 34–44. [Google Scholar] [CrossRef]
- Rama, M.K.; Achari, V.B.S.; Rao, V.V.R.N.; Sharma, A.K. Electrical and optical properties of (PEMA/PVC) polymer blend electrolyte doped with NaClO4. Polym. Test. 2011, 30, 881–886. [Google Scholar] [CrossRef]
- Aziz, S.B.; Ahmed, H.M.; Hussein, A.M.; Fathulla, A.B.; Wsw, R.M.; Hussein, R.T. Tuning the absorption of ultraviolet spectra and optical parameters of aluminum doped PVA based solid polymer composites. J. Mater. Sci. Mater. Electron. 2015, 26, 8022. [Google Scholar] [CrossRef]
- Brza, M.A.; Aziz, S.B.; Anuar, H.; Al Hazza, M.F. From green remediation to polymer hybrid fabrication with improved optical band gaps. Int. J. Mol. Sci. 2019, 20, 3910. [Google Scholar] [CrossRef] [Green Version]
- Aziz, S.B.; Abdulwahid, R.T.; Rsaul, H.A.; Ahmed, H.M. In situ synthesis of CuS nanoparticle with a distinguishable SPR peak in NIR region. J. Mater. Sci. Mater. Electron. 2016, 27, 4163. [Google Scholar] [CrossRef]
- Aziz, S.B.; Abdullah, O.G.; Rasheed, M.A. A novel polymer composite with a small optical band gap: New approaches for photonics and optoelectronics. J. Appl. Polym. Sci. 2017, 134, 44847. [Google Scholar] [CrossRef]
- Aziz, S.B.; Hussein, S.; Hussein, A.M.; Saeed, S.R. Optical characteristics of polystyrene based solid polymer composites: Effect of metallic copper powder. Int. J. Met. 2013, 2013, 123657. [Google Scholar] [CrossRef]
- Cardona, M. Light Scattering in Solids I, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar] [CrossRef]
- Träger, F. Springer Handbook of Lasers and Optics; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Bower, D.I. Infrared dichroism, polarized fluorescence and Raman spectroscopy. In Structure and Properties of Oriented Polymers, 1st ed.; Springer: Dordrecht, The Netherlands, 1997; pp. 181–233. [Google Scholar] [CrossRef]
- Manjunatha, V.; Subramanya, K.; Devendrappa, H. Structural optical and electrical conductivity properties of Li2SO4 doped polymer electrolytes. Compos. Interfaces 2014, 21, 121–131. [Google Scholar] [CrossRef]
- Uratani, Y.; Shishidou, T.; Oguchi, T. First-principles study of lead-free piezoelectric SnTiO3. Jpn. J. Appl. Phys. 2008, 47, 7735–7739. [Google Scholar] [CrossRef]
- Matar, S.F.; Baraille, I.; Subramaniam, M.A. First principles studies of SnTiO3 perovskite as potential environmentally benign ferroelectric material. Chem. Phys. 2009, 355, 43–49. [Google Scholar] [CrossRef]
- Scott, J.F.; Paz de Araujo, C.A. Ferroelectric Memories. Science 1989, 246, 1400–1405. [Google Scholar] [CrossRef] [PubMed]
- Jiwei, Z.; Xi, Y.; Liangying, Z. The optical waveguide characteristics of highly orientated sol–gel derived polycrystalline ferroelectric PZT thin films. Ceram. Int. 2001, 27, 585–589. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, B.; Woo, C.H. Piezoelectric bending response and switching behavior of ferroelectric/paraelectric bilayers. Acta Mater. 2008, 56, 479–488. [Google Scholar] [CrossRef]
- Aziz, S.B.; Rasheed, M.A.; Hussein, A.M.; Ahmed, H.M. Fabrication of polymer blend composites based on [PVA-PVP](1−x):(Ag2S)x (0.01 ≤ x ≤ 0.03) with small optical band gaps: Structural and optical properties. Mater. Sci. Semicond. Process. 2017, 71, 197–203. [Google Scholar] [CrossRef]
- Aziz, S.B.; Hassan, A.Q.; Mohammed, S.J.; Karim, W.O.; Kadir, M.F.Z.; Tajuddin, H.A.; Chan, N.N.M.Y. Structural and optical characteristics of PVA: C-Dot composites: Tuning the absorption of ultra violet (UV) region. Nanomaterials 2019, 9, 216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, A.; Jangir, L.K.; Kumari, Y.; Kumar, M.; Kumar, V.; Awasthi, K. Optical and Structural Study of Polyaniline/Polystyrene Composite Films. Macromol. Symp. 2015, 357, 229–234. [Google Scholar] [CrossRef]
- Aziz, S.B.; Abdullah, R.M. Crystalline and amorphous phase identification from the tanδ relaxation peaks and impedance plots in polymer blend electrolytes based on [CS: AgNt] x: PEO (x-1)(10≤ x≤ 50). Electrochim. Acta 2018, 285, 30–46. [Google Scholar] [CrossRef]
- Hou, X.; Ying, H. Fabrication of Polystyrene/Detonation Nanographite Composite Microspheres with the Core/Shell Structure via Pickering Emulsion Polymerization. J. Nanomater. 2013, 2013, 751497. [Google Scholar] [CrossRef]
- Yusuf, S.N.F.; Azzahari, A.D.; Yahya, R.; Majid, S.R.; Careem, M.A.; Arof, A.K. From crab shell to solar cell: A gel polymer electrolyte based on N-phthaloylchitosan and its application in dye-sensitized solar cells. RSC Adv. 2016, 6, 27714–27724. [Google Scholar] [CrossRef]
- Al Juhaiman, L.A.; Al-Enezi, D.A.; Mekhamer, W.K. Preparation and characterization of polystyrene/organoclay nanocomposites from raw clay. Dig. J. Nanomater. Biostruct. 2016, 11, 105–114. [Google Scholar]
- Saini, I.; Rozra, J.; Chandak, N.; Aggarwal, S.; Sharma, P.K.; Sharma, A. Tailoring of electrical, optical and structural properties of PVA by additionof Ag nanoparticles. Mater. Chem. Phys. 2013, 139, 802–810. [Google Scholar] [CrossRef]
- Niculaescu, C.; Olar, L.; Stefan, R.; Todica, M.; Pop, C. XRD and IR investigationofsomecommercial Polystyrene samples thermally degraded. Studia UBB Chem. 2018, 63, 63–70. [Google Scholar] [CrossRef]
- Verma, M.L.; Minakshi, M.; Singh, N.K. Synthesis and characterization of solid polymer electrolyte based on activated carbon for solid state capacitor. Electrochim. Acta 2014, 137, 497–503. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, D.M.T.; Rostam, S.; Aziz, S.B. A Comparative Study on Structural, Morphological, and Tensile Properties of Binary and Ternary Epoxy Resin-Based Polymer Nanocomposites. Adv. Mater. Sci. Eng. 2020, 2020, 7914796. [Google Scholar] [CrossRef]
- Verma, M.L.; Minakshi, M.; Singh, N.K. Structural and electrochemical properties of nanocomposite polymer electrolyte for electrochemical devices. Ind. Eng. Chem. Res. 2014, 53, 14993–15001. [Google Scholar] [CrossRef]
- Aziz, S.B. Role of dielectric constant on ion transport: Reformulated Arrhenius equation. Adv. Mater. Sci. Eng. 2016, 2016, 2527013. [Google Scholar] [CrossRef] [Green Version]
- Aziz, S.B.; Abidin, Z.H.Z. Ion-transport study in nanocomposite solid polymer electrolytes based on chitosan: Electrical and dielectric analysis. J. Appl. Polym. Sci. 2015, 132, 1–10. [Google Scholar] [CrossRef]
- Stefanescu, E.A.; Daranga, C.; Stefanescu, C. Insight into the Broad Field of Polymer Nanocomposites: From Carbon Nanotubes to Clay Nanoplatelets, via Metal Nanoparticles. Materials 2009, 2, 2095–2153. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Al-Ghamdi, A.A.; Sharma, G.D.; El Mansy, M.K. Effect of ethylene carbonate as a plasticizer on CuI/PVA nanocomposite: Structure, optical and electrical properties. J. Adv. Res. 2014, 5, 79–86. [Google Scholar] [CrossRef] [Green Version]
- Rahman, E.S.; Ahmmad, S.K.; Gupta, A.; Kumar, K.S. Optical properties of amorphous Li2O–WO3–B2O3 thin films deposited by electron beam evaporation. J. Taibah Univ. Sci. 2016, 10, 363–368. [Google Scholar]
- Aziz, S.B.; Abdullah, O.G.; Hussein, A.M.; Ahmed, H.M. From Insulating PMMA Polymer to Conjugated Double Bond Behavior: Green Chemistry as a Novel Approach to Fabricate Small Band Gap Polymers. Polymers 2017, 9, 626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wooten, F. Optical Properties of Solids; Academic Press: New York, NY, USA; London, UK, 1972. [Google Scholar]
- Aziz, S.B.; Abdullah, O.G.; Hussein, A.M.; Abdulwahid, R.T.; Rasheed, M.A.; Ahmed, H.M.; Abdalqadir, S.W.; Mohammed, A.R. Optical properties of pure and doped PVA: PEO based solid polymer blend electrolytes: Two methods for band gap study. J. Mater. Sci. Mater. Electron. 2017, 28, 7473. [Google Scholar] [CrossRef]
- Fritsch, J.; Mansfeld, D.; Mehring, M.; Wursche, R.; Grothe, J.; Kaskel, S. Refractive index tuning of highly transparent bismuth containing polymer composites. Polymer 2011, 52, 3263–3268. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids, 3rd ed.; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Caseri, W. Nanocomposites of polymers and metals or semiconductors: Historical background and optical properties. Macromol. Rapid Commun. 2000, 21, 705–722. [Google Scholar] [CrossRef]
- Jin, J.; Qi, R.; Su, Y.; Tong, M.; Zhu, J. Preparation of high-refractive-index PMMA/TiO2 nanocomposites by one-step in situ solvothermal method. Iran. Polym. J. 2013, 22, 767–774. [Google Scholar] [CrossRef]
- Muhammad, F.F.; Aziz, S.B.; Hussein, S.A. Effect of the dopant salt on the optical parameters of PVA:NaNO3solid polymer electrolyte. J. Mater. Sci. Mater. Electron. 2015, 26, 521–529. [Google Scholar] [CrossRef]
- Tao, P.; Li, Y.; Rungta, A.; Viswanath, A.; Gao, J.; Benicewicz, B.C.; Siegel, R.W.; Schadler, L.S. TiO2 nanocomposites with high refractive index and transparency. J. Mater. Chem. 2011, 21, 18623. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, Z.; Mahoney, C.; Yan, J.; Ferebee, R.; Luo, D.; Matyjaszewski, K.; Bockstaller, M.R. Transparent and High Refractive Index Thermoplastic Polymer Glasses Using Evaporative Ligand Exchange of Hybrid Particle Fillers. ACS Appl. Mater. Interfaces 2017, 9, 7515–7522. [Google Scholar] [CrossRef]
- Aziz, S.B. Modifying poly (vinyl alcohol)(PVA) from insulator to small-bandgap polymer: A novel approach for organic solar cells and optoelectronic devices. J. Electron. Mater. 2016, 45, 736–745. [Google Scholar] [CrossRef]
- Biskri, Z.E.; Rached, H.; Bouchear, M.; Rached, D.; Aida, M.S. A Comparative Study of Structural Stability and Mechanical and Optical Properties of Fluorapatite (Ca5(PO4)3F) and Lithium Disilicate (Li2Si2O5) Components Forming Dental Glass–Ceramics: First Principles Study. J. Electron. Mater. 2016, 45, 5082–5095. [Google Scholar] [CrossRef]
- Ravindra, N.M.; Ganapathy, P.; Choi, J. Energy gap–refractive index relations in semiconductors—An overview. Infrared Phys. Technol. 2007, 50, 21–29. [Google Scholar] [CrossRef]
- Plass, M.F.; Popov, C.; Ivanov, B.; Mänd, S.; Jelinek, M.; Zambov, L.M.; Kulisch, W. Correlation between photoluminescence, optical and structuralproperties of amorphous nitrogen-rich carbon nitride films. Appl. Phys. A 2001, 72, 21–27. [Google Scholar] [CrossRef]
- Jacob, R.; Harikrishnan, J.I.; Nair, G. Optical band gap analysis of nano-crystalline ceramic PbSrCaCuO. J. Adv. Phys. 2014, 5, 816–822. [Google Scholar] [CrossRef]
- Yakuphanoglu, F.; Arslan, M. Determination of electrical conduction mechanism and optical band gap of a new charge transfer complex: TCNQ-PANT. Solid State Commun. 2004, 132, 229–234. [Google Scholar] [CrossRef]
- Muhammed, D.S.; Brza, M.A.; Nofal, M.M.; Aziz, S.B.; Hussen, S.A.; Abdulwahid, R.T. Optical Dielectric Loss as a Novel Approach to Specify the Types of Electron Transition: XRD and UV-Vis as a Non-Destructive Techniques for Structural and Optical Characterization of PEO Based Nanocomposites. Materials 2020, 13, 2979. [Google Scholar] [CrossRef] [PubMed]
- Aziz, S. Morphological and Optical Characteristics of Chitosan(1−x):Cuox (4 ≤ x ≤ 12) Based Polymer nanocomposites: Optical Dielectric Loss as an Alternative Method for Tauc’s Model. Nanomaterials 2017, 7, 444. [Google Scholar] [CrossRef] [Green Version]
- Aziz, S.B.; Abdullah, O.; Brza, M.A.; Azawy, A.K.; Tahir, D.A. Effect of Carbon Nano-dots (CNDs) on Structural and Optical Properties of PMMA Polymer Composite. Results Phys. 2019, 102776. [Google Scholar] [CrossRef]
- Aziz, S.B.; Rasheed, M.A.; Ahmed, H.M. Synthesis of Polymer Nanocomposites Based on [Methyl Cellulose](1− x):(CuS) x (0.02 M≤ x≤ 0.08 M) with Desired Optical Band Gaps. Polymers 2017, 9, 194. [Google Scholar] [CrossRef]
- Aziz, S.B.; Mamand, S.M.; Saed, S.R.; Abdullah, R.M.; Hussein, S.A. New Method for the Development of Plasmonic Metal-Semiconductor Interface Layer: Polymer Composites with Reduced Energy Band Gap. J. Nanomater. 2017, 2017, 8140693. [Google Scholar] [CrossRef] [Green Version]
- Cui-E, H.; Zhao-Yi, Z.; Yan, C.; Xiang-Rong, C.; Ling-Cang, C. First-principles calculations for electronic, optical and thermodynamic properties of ZnS. Chin. Phys. B 2008, 17, 3867–3874. [Google Scholar] [CrossRef]
- Rahman, A.; Rahman, A.; Chowdhury, U.K.; Bhuiyan, M.T.H.; Ali, L.; Sarker, A.R. First principles investigation of structural, elastic, electronic and optical properties of ABi2O6 (A = Mg,Zn) with trirutile-type structure. Cogent Phys. 2016, 3, 1257414. [Google Scholar] [CrossRef]
- Nasr, T.B.; Maghraoui-Meherzi, H.; Abdallah, H.B.; Bennaceur, R. First principles calculations of electronic and optical properties of Ag2S. Solid State Sci. 2013, 26, 65–71. [Google Scholar] [CrossRef]
- Taib, M.F.M.; Yaakob, M.K.; Hassan, O.H.; Yahya, M.Z.A. First Principles Calculation on Elastic, Electronic and Optical Properties of new cubic (Pm3m) Pb-free Perovskite Oxide of SnZrO3. In Proceedings of the IEEE Symposium on Business, Engineering and Industrial Applications, Bandung, Indonesia, 23–26 September 2012; pp. 13–17. [Google Scholar]
- Thutupallit, G.K.M.; Tomlin, S.G. The optical properties of thin films of cadmium and zinc selenides and tellurides. J. Phys. D Appl. Phys. 1976, 9, 1639–1646. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Wang, Y.H.; Zhang, M.; Zhao, N.; Gong, S.; Chen, Q. First-Principles Calculations of the Structural, Electronic and Optical Properties of BaZrxTi1−xO3 (x = 0, 0.25, 0.5, 0.75). Chin. Phys. Lett. 2011, 28, 067101. [Google Scholar] [CrossRef]
- Ching, W.Y.; Gu, Z.Q.; Xu, Y.N. First-principles calculation of the electronic and optical properties of LiNb03. Phys. Rev. B 1992, 50, 1992–1995. [Google Scholar] [CrossRef]
- Cheddadi, S.; Boubendira, K.; Meradji, H.; Ghemid, S.; Hassan, F.E.H.; Lakel, S.; Khenata, R. First-principle calculations of structural, electronic, optical, elastic and thermal properties of MgXAs2 (X = Si, Ge) compounds. Pramana J. Phys. 2017, 89, 89. [Google Scholar] [CrossRef]
- Meftah, A.M.; Gharibshahi, E.; Soltani, N.; Yunus, W.M.M.; Saion, E. Structural, optical and electrical properties of PVA/PANI/Nickel nanocomposites synthesized by gamma radiolytic method. Polymers 2014, 6, 2435–2450. [Google Scholar] [CrossRef] [Green Version]
- Aziz, S.B.; Brza, M.A.; Nofal, M.M.; Abdulwahid, R.T.; Hussen, S.A.; Hussein, A.M.; Karim, W.O. A Comprehensive Review on Optical Properties of Polymer Electrolytes and Composites. Materials 2020, 13, 3675. [Google Scholar] [CrossRef]
- Balestrieri, M. Transparent Conductive Oxides with Photon Converting Properties in View of Photovoltaic Applications: The Cases of Rare Earth-Doped Zinc Oxide and Cerium Oxide. Ph.D. Thesis, Université de Strasbourg, Strasbourg, France, 2015. [Google Scholar]
- Aziz, S.B.; Rasheed, M.A.; Abidin, Z.H.Z. Optical and Electrical Characteristics of Silver Ion Conducting Nanocomposite Solid Polymer Electrolytes Based on Chitosan. J. Electron. Mater. 2017, 46, 6119–6130. [Google Scholar] [CrossRef]
- Li, L.; Wang, W.; Liu, H.; Liu, X.; Song, Q.; Ren, S. First Principles Calculations of Electronic Band Structure and Optical Properties of Cr-Doped ZnO. J. Phys. Chem. C 2009, 113, 8460–8464. [Google Scholar] [CrossRef]
- Rocquefelte, X.; Jobic, S.; Whangbo, M.H. Concept of optical channel as a guide for tuning the optical properties of insulating materials. Solid State Sci. 2007, 9, 600–603. [Google Scholar] [CrossRef]
- Rodríguez, A.; Vergara, M.E.S.; Montalvo, V.G.; Ortiz, A.; Alvarez, J.R. “Thin films of molecular materials synthesized from C32H20N10M (M = Co, Pb, Fe): Film formation, electrical and optical properties. Appl. Surf. Sci. 2010, 256, 3374–3379. [Google Scholar] [CrossRef]
- Hossain, F.M.; Sheppard, L.; Nowotny, J.; Murch, G.E. Optical properties of anatase and rutile titanium dioxide: Ab initio calculations for pure and anion-doped material. J. Phys. Chem. Solids 2008, 69, 1820–1828. [Google Scholar] [CrossRef]















| 2θ Degree | cos θ | D (nm) | DAverage (nm) |
|---|---|---|---|
| 30.85° | 0.963 | 20.85 | 25.179 |
| 32.15° | 0.96 | 33.19 | |
| 44.05° | 0.927 | 24.91 | |
| 45.05° | 0.923 | 21.76 |
| Sample Code | FWHM |
|---|---|
| PSSNT0 | 0.963 |
| PSSNT1 | 0.96 |
| PSSNT2 | 0.923 |
| Sample Code | Absorption Edge (eV) |
|---|---|
| PSSNT0 | 4.4 |
| PSSNT1 | 3.7 |
| PSSNT2 | 3.4 |
| Composition | Refractive Index | Ref. |
|---|---|---|
| PMMA: TiO2 | 1.839 | [50] |
| PGMA: TiO2 | 1.8 | [52] |
| PMMA: ZnO | ≈1.65 | [53] |
| PVA: Al powder | 2.14 | [13] |
| PVA-Cu(II)-complex | 1.6 | [14] |
| PS: SnTiO3 | 2.6 | This work |
| Sample Code | Eg for γ = 1/2 | Eg for γ = 2 | Eg for γ = 3 | Eg for γ = 3/2 | Eg from ɛi plot |
|---|---|---|---|---|---|
| PSSNT0 | 4.44 | 4.39 | 4.24 | 4.35 | 4.42 |
| PSSNT1 | 3.94 | 3.75 | 3.38 | 3.76 | 3.78 |
| PSSNT2 | 3.64 | 3.4 | 3.2 | 3.27 | 3.25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussein, A.M.; Dannoun, E.M.A.; Aziz, S.B.; Brza, M.A.; Abdulwahid, R.T.; Hussen, S.A.; Rostam, S.; Mustafa, D.M.T.; Muhammad, D.S. Steps Toward the Band Gap Identification in Polystyrene Based Solid Polymer Nanocomposites Integrated with Tin Titanate Nanoparticles. Polymers 2020, 12, 2320. https://doi.org/10.3390/polym12102320
Hussein AM, Dannoun EMA, Aziz SB, Brza MA, Abdulwahid RT, Hussen SA, Rostam S, Mustafa DMT, Muhammad DS. Steps Toward the Band Gap Identification in Polystyrene Based Solid Polymer Nanocomposites Integrated with Tin Titanate Nanoparticles. Polymers. 2020; 12(10):2320. https://doi.org/10.3390/polym12102320
Chicago/Turabian StyleHussein, Ahang M., Elham M. A. Dannoun, Shujahadeen B. Aziz, Mohamad A. Brza, Rebar T. Abdulwahid, Sarkawt A. Hussen, Sarkawt Rostam, Dalia M. T. Mustafa, and Dana S. Muhammad. 2020. "Steps Toward the Band Gap Identification in Polystyrene Based Solid Polymer Nanocomposites Integrated with Tin Titanate Nanoparticles" Polymers 12, no. 10: 2320. https://doi.org/10.3390/polym12102320
APA StyleHussein, A. M., Dannoun, E. M. A., Aziz, S. B., Brza, M. A., Abdulwahid, R. T., Hussen, S. A., Rostam, S., Mustafa, D. M. T., & Muhammad, D. S. (2020). Steps Toward the Band Gap Identification in Polystyrene Based Solid Polymer Nanocomposites Integrated with Tin Titanate Nanoparticles. Polymers, 12(10), 2320. https://doi.org/10.3390/polym12102320