Energy Utilization of Building Insulation Waste Expanded Polystyrene: Pyrolysis Kinetic Estimation by a New Comprehensive Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Thermogravimetric Measurements
2.3. Pyrolysis Kinetics
2.4. Methods
2.4.1. Flynn–Wall–Ozawa Method (FWO)
2.4.2. Coats–Redfern Method (CR)
2.4.3. Global Optimization Method-PSO
3. Results and Discussion
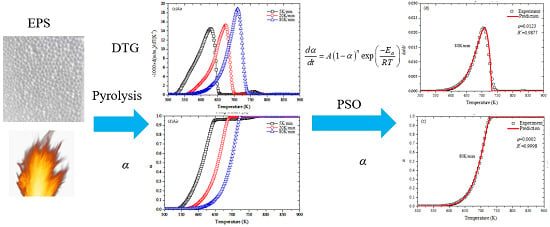
3.1. Thermogravimetric Analysis
3.2. Kinetic Analysis by the FWO Method
3.3. Establish Reaction Mechanisms
3.4. Parameters Optimization by PSO
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pichler, C.; Metzler, G.; Niederegger, C.; Lackner, R. Thermo-mechanical optimization of porous building materials based on micromechanical concepts: Application to load-carrying insulation materials. Compos. B Eng. 2012, 43, 1015–1023. [Google Scholar] [CrossRef]
- Rao, V.V.; Parameshwaran, R.; Ram, V.V. PCM-mortar based construction materials for energy efficient buildings: A review on research trends. Energy Build. 2018, 158, 95–122. [Google Scholar] [CrossRef]
- Hong, T.; Chen, Y.; Luo, X.; Luo, N.; Lee, S.H. Ten questions on urban building energy modeling. Build. Environ. 2020, 168, 106508. [Google Scholar] [CrossRef] [Green Version]
- Cárdenas-R, J.P.; Cea, M.; Santín, K.; Valdés, G.; Hunter, R.; Navia, R. Characterization and application of a natural polymer obtained from Hydrangea macrophylla as a thermal insulation biomaterial. Compos. B Eng. 2018, 132, S1359836816311155. [Google Scholar] [CrossRef]
- Park, H.S.; Kim, Y.; Oh, B.K.; Cho, T. Compressive properties of graphite-embedded expanded polystyrene for vibroacoustic engineering applications. Compos. B Eng. 2016, 93, S1359836816300282. [Google Scholar] [CrossRef]
- Rajak, A.; Hapidin, D.A.; Iskandar, F.; Munir, M.M.; Khairurrijal, K. Electrospun nanofiber from various source of expanded polystyrene (EPS) waste and their characterization as potential air filter media. Waste Manag. 2020, 103, 76–86. [Google Scholar] [CrossRef]
- Lahtela, V.; Hyvarinen, M.; Karki, T. Composition of plastic fractions in waste streams: Toward more efficient recycling and utilization. Polymers 2019, 11, 69. [Google Scholar] [CrossRef] [Green Version]
- Fernando, P.; Jayasinghe, M.; Jayasinghe, C. Structural feasibility of expanded polystyrene (EPS) based lightweight concrete sandwich wall panels. Constr. Build. Mater. 2017, 139, 45–51. [Google Scholar] [CrossRef]
- Chauhan, R.; Gopinath, S.; Razdan, P.; Delattre, C.; Nirmala, G.; Natarajan, R. Thermal decomposition of expanded polystyrene in a pebble bed reactor to get higher liquid fraction yield at low temperatures. Waste Manag. 2008, 28, 2140–2145. [Google Scholar] [CrossRef]
- Johnston, B.; Radecka, I.; Hill, D.; Chiellini, E.; Ilieva, V.I.; Sikorska, W.; Musiol, M.; Zieba, M.; Marek, A.A.; Keddie, D. The microbial production of polyhydroxyalkanoates from waste polystyrene fragments attained using oxidative degradation. Polymers 2018, 10, 957. [Google Scholar] [CrossRef] [Green Version]
- Gomezrojo, R.; Alameda, L.; Rodriguez, A.; Calderon, V.; Gutierrezgonzalez, S. Characterization of polyurethane foam waste for reuse in eco-efficient building materials. Polymers 2019, 11, 359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abnisa, F.; Sharuddin, S.D.A.; Zanil, M.; Daud, W.M.; Mahlia, T.M. The yield prediction of synthetic fuel production from pyrolysis of plastic waste by levenberg–Marquardt approach in feedforward neural networks model. Polymers 2019, 11, 1853. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Xu, X.; Zhang, Y.; Lo, S.; Lu, S. Kinetic study on pyrolysis of waste phenolic fibre-reinforced plastic. Appl. Therm. Eng. 2018, 136, 484–491. [Google Scholar] [CrossRef]
- Li, M.; Liu, L.; Jiang, L.; Gou, F.; Sun, J. Application of distributed activation energy models to polymer pyrolysis: Effects of distributed model selection, characteristics, validation, and sensitivity analysis. Fuel 2019, 254, 115594. [Google Scholar] [CrossRef]
- Zhou, Y.; Bu, R.; Gong, J.; Yan, W.; Fan, C. Experimental investigation on downward flame spread over rigid polyurethane and extruded polystyrene foams. Exp. Therm. Fluid Sci. 2018, 92, 346–352. [Google Scholar] [CrossRef]
- Si, J.; Tawiah, B.; Sun, W.; Lin, B.; Wang, C.; Yuen, A.C.Y.; Yu, B.; Li, A.; Yang, W.; Lu, H. Functionalization of MXene nanosheets for polystyrene towards high thermal stability and flame retardant properties. Polymers 2019, 11, 976. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernandez, A.; Saffe, A.; Pereyra, R.; Mazza, G.; Rodriguez, R. Kinetic study of regional agro-industrial wastes pyrolysis using non-isothermal TGA analysis. Appl. Therm. Eng. 2016, 106, 1157–1164. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Liu, P.; Jing, Z.; Ge, X.; Jiang, Y. The flame resistance properties of expandable polystyrene foams coated with a cheap and effective barrier layer. Constr. Build. Mater. 2018, 176, 403–414. [Google Scholar] [CrossRef]
- Nisar, J.; Ali, G.; Shah, A.; Iqbal, M.; Khan, R.A.; Anwar, F.; Ullah, R.; Akhter, M.S. Fuel production from waste polystyrene via pyrolysis: Kinetics and products distribution. Waste Manag. 2019, 88, 236–247. [Google Scholar] [CrossRef]
- Jiao, L.; Xu, G.; Wang, Q.; Xu, Q.; Sun, J. Kinetics and volatile products of thermal degradation of building insulation materials. Thermochim. Acta 2012, 547, 120–125. [Google Scholar] [CrossRef]
- Azimi, H.R.; Rezaei, M.; Abbasi, F.; Charchi, A.; Bahluli, Y. Non-isothermal degradation kinetics of MMA-St copolymer and EPS lost foams. Thermochim. Acta 2008, 474, 72–77. [Google Scholar] [CrossRef]
- Kannan, P.; Biernacki, J.J.; Visco, D.P., Jr.; Lambert, W. Kinetics of thermal decomposition of expandable polystyrene in different gaseous environments. J. Anal. Appl. Pyrolysis 2009, 84, 139–144. [Google Scholar] [CrossRef]
- Jun, H.C.; Oh, S.C.; Lee, H.P.; Kim, H.T. A kinetic analysis of the thermal-oxidative decomposition of expandable polystyrene. Korean J. Chem. Eng. 2006, 23, 761–766. [Google Scholar] [CrossRef]
- Jiang, L.; Xiao, H.; He, J.; Sun, Q.; Gong, L.; Sun, J. Application of genetic algorithm to pyrolysis of typical polymers. Fuel Process. Technol. 2015, 138, 48–55. [Google Scholar] [CrossRef]
- Xiao, R.; Yang, W.; Cong, X.; Dong, K.; Xu, J.; Wang, D.; Yang, X. Thermogravimetric analysis and reaction kinetics of lignocellulosic biomass pyrolysis. Energy 2020, 201, 117537. [Google Scholar] [CrossRef]
- Ding, Y.; Fukumoto, K.; Ezekoye, O.A.; Lu, S.; Wang, C.; Li, C. Experimental and numerical simulation of multi-component combustion of typical charring material. Combust. Flame 2020, 211, 417–429. [Google Scholar] [CrossRef]
- Ding, Y.; Ezekoye, O.A.; Zhang, J.; Wang, C.; Lu, S. The effect of chemical reaction kinetic parameters on the bench-scale pyrolysis of lignocellulosic biomass. Fuel 2018, 232, 147–153. [Google Scholar] [CrossRef]
- Ding, Y.; Huang, B.; Li, K.; Du, W.; Lu, K.; Zhang, Y. Thermal interaction analysis of isolated hemicellulose and cellulose by kinetic parameters during biomass pyrolysis. Energy 2020, 195, 117010. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Y.; Zhang, J.; Zhou, R.; Ren, Z.; Guo, H. Kinetic parameters estimation of pinus sylvestris pyrolysis by Kissinger-Kai method coupled with particle swarm optimization and global sensitivity analysis. Bioresour. Technol. 2019, 293, 122079. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, W.; Yu, L.; Lu, K. The accuracy and efficiency of GA and PSO optimization schemes on estimating reaction kinetic parameters of biomass pyrolysis. Energy 2019, 176, 582–588. [Google Scholar] [CrossRef]
- Kannan, P.; Biernacki, J.J.; Visco, D.P., Jr. A review of physical and kinetic models of thermal degradation of expanded polystyrene foam and their application to the lost foam casting process. J. Anal. Appl. Pyrolysis 2007, 78, 162–171. [Google Scholar] [CrossRef]
- Dixit, A.; Dai Pang, S.; Kang, S.H.; Moon, J. Lightweight structural cement composites with expanded polystyrene (EPS) for enhanced thermal insulation. Cem. Concr. Compos. 2019, 102, 185–197. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, J.; Tang, G.; Zhang, Y.; Sun, J. Effects of altitude and inclination on the flame structure over the insulation material PS based on heat and mass transfer. Int. J. Heat Mass Transf. 2015, 90, 1046–1055. [Google Scholar] [CrossRef]
- Jiao, L.; Sun, J. A thermal degradation study of insulation materials extruded polystyrene. Procedia Eng. 2014, 71, 622–628. [Google Scholar] [CrossRef] [Green Version]
- Doroudiani, S.; Omidian, H. Environmental, health and safety concerns of decorative mouldings made of expanded polystyrene in buildings. Build. Environ. 2010, 45, 647–654. [Google Scholar] [CrossRef]
- Gao, X.; Jiang, L.; Xu, Q. Experimental and theoretical study on thermal kinetics and reactive mechanism of nitrocellulose pyrolysis by traditional multi kinetics and modeling reconstruction. J Hazard Mater. 2020, 386, 121645. [Google Scholar] [CrossRef]
- Slopiecka, K.; Bartocci, P.; Fantozzi, F. Thermogravimetric analysis and kinetic study of poplar wood pyrolysis. Appl. Energy 2012, 97, 491–497. [Google Scholar] [CrossRef]
- Venkatesh, M.; Ravi, P.; Tewari, S.P. Isoconversional kinetic analysis of decomposition of nitroimidazoles: Friedman method vs. Flynn-Wall-Ozawa method. J. Phys. Chem. A 2013, 11, 10162–10169. [Google Scholar] [CrossRef]
- Kong, D.; Peng, R.; Sun, X.; Zhang, J.; Ping, P.; Du, J. Study of the influence of crude oil on the spontaneous combustion risk of sulfurized rust in crude oil tanks. Fuel 2019, 255, 115816. [Google Scholar] [CrossRef]
- Doyle, C.D. Kinetic analysis of thermogravimetric data. J. Appl. Polym. Sci. 1961, 5, 285–292. [Google Scholar] [CrossRef]
- Coats, A.W.; Redfern, J. Kinetic parameters from thermogravimetric data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Gao, X.; Jiang, L.; Xu, Q.; Wu, W.Q.; Mensah, R.A. Thermal kinetics and reactive mechanism of cellulose nitrate decomposition by traditional multi kinetics and modeling calculation under isothermal and non-isothermal conditions. Ind. Crops Prod. 2020, 145, 112085. [Google Scholar] [CrossRef]
- Vlaev, L.; Nedelchev, N.; Gyurova, K.; Zagorcheva, M. A comparative study of non-isothermal kinetics of decomposition of calcium oxalate monohydrate. J. Anal. Appl. Pyrolysis 2008, 81, 253–262. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, J.; Wu, S.; Wang, B.; Wang, Z. Pyrolysis kinetics of phenol–formaldehyde resin by non-isothermal thermogravimetry. Carbon 2010, 48, 352–358. [Google Scholar] [CrossRef]
- Xu, L.; Jiang, Y.; Wang, L. Thermal decomposition of rape straw: Pyrolysis modeling and kinetic study via particle swarm optimization. Energy Convers. Manag. 2017, 146, 124–133. [Google Scholar] [CrossRef]
- Liu, Y.; Bakhtiyarov, S.I.; Overfelt, R.A. Numerical modeling and experimental verification of mold filling and evolved gas pressure in lost foam casting process. J. Mater. Sci. 2002, 37, 2997–3003. [Google Scholar] [CrossRef]
- Ding, Y.; Huang, B.; Wu, C.; He, Q.; Lu, K. Kinetic model and parameters study of lignocellulosic biomass oxidative pyrolysis. Energy 2019, 181, 11–17. [Google Scholar] [CrossRef]
- Ding, Y.; Ezekoye, O.A.; Lu, S.; Wang, C.; Zhou, R. Comparative pyrolysis behaviors and reaction mechanisms of hardwood and softwood. Energy Convers. Manag. 2017, 132, 102–109. [Google Scholar] [CrossRef]
- Chen, R.; Li, Q.; Xu, X.; Zhang, D. Pyrolysis kinetics and reaction mechanism of representative non-charring polymer waste with micron particle size. Energy Convers. Manag. 2019, 198, 111923. [Google Scholar] [CrossRef]




| g(α) | f(α) | Rate-Determining Mechanism |
|---|---|---|
| α | 1 | Contracting disk |
| 1 − (1 − α)1/2 | 2(1 − α)1/2 | Contracting area |
| 1 − (1 − α)1/3 | 3(1 − α)2/3 | Contracting volume |
| 1 − (1 − α)1/4 | 4(1 − α)3/4 | Chemical reaction |
| 1 − (1 − α)2 | 1/2(1 − α)−1 | Chemical reaction |
| 1 − (1 − α)3 | 1/3(1 − α)−2 | Chemical reaction |
| α2 | 1/(2α) | 1-D diffusion |
| (1 − α)ln(1 − α) + α | [−ln(1 − α)]−1 | 2-D diffusion |
| [1 − (1 − α)1/3]1/2 | 6(1 − α)2/3[1 − (1 − α)1/3]1/2 | 3-D diffusion |
| β (K/min) | Peak Temperature (K) | |||
|---|---|---|---|---|
| Calculated Values | Kannan et al. [22] | Experimental Values (N2) | Experimental Values (Air) | |
| 5 | 672 | 673 | 671 | 628 |
| 20 | 705 | 703 | 699 | 674 |
| 80 | 741 | - | 735 | 710 |
| α | N2 | Air | ||||
|---|---|---|---|---|---|---|
| Ea (kJ/mol) | R2 | lnA [ln(s−1)] | Ea (kJ/mol) | R2 | lnA [ln(s−1)] | |
| g(α) = 1 − (1 − α)3 | g(α) = 1 − (1 − α)1/4 | |||||
| 0.10 | 153.79 | 0.979 | 21.91 | 98.83 | 0.993 | 11.84 |
| 0.20 | 162.32 | 0.985 | 23.63 | 98.97 | 0.986 | 12.00 |
| 0.30 | 162.32 | 0.985 | 23.68 | 102.50 | 0.982 | 12.72 |
| 0.40 | 163.64 | 0.987 | 23.91 | 106.97 | 0.982 | 13.60 |
| 0.50 | 164.98 | 0.988 | 24.10 | 110.94 | 0.985 | 14.37 |
| 0.60 | 166.33 | 0.989 | 24.27 | 115.08 | 0.986 | 15.15 |
| 0.70 | 166.10 | 0.986 | 24.11 | 120.24 | 0.984 | 16.13 |
| 0.80 | 166.33 | 0.989 | 24.02 | 125.20 | 0.986 | 17.06 |
| Average | 163.23 | 0.986 | 23.70 | 109.85 | 0.986 | 14.11 |
| Reaction Model | Average Value (N2) | Average Value (Air) | ||
|---|---|---|---|---|
| g(α) | Ea (kJ/mol) | R2 | Ea (kJ/mol) | R2 |
| α | 238.00 | 0.985 | 95.03 | 0.995 |
| 1 − (1 − α)1/2 | 274.12 | 0.994 | 85.64 | 0.998 |
| 1 − (1 − α)1/3 | 287.34 | 0.995 | 86.99 | 0.997 |
| 1 − (1 − α)1/4 | 295.74 | 0.996 | 105.14 | 0.996 |
| 1 − (1 − α)2 | 182.05 | 0.952 | 66.61 | 0.969 |
| 1 − (1 − α)3 | 158.17 | 0.902 | 62.08 | 0.918 |
| α2 | 371.42 | 0.986 | 160.76 | 0.996 |
| (1 − α)ln(1 − α) + α | 532.55 | 0.992 | 219.33 | 0.998 |
| [1 − (1 − α)1/3]1/2 | 138.70 | 0.995 | 52.60 | 0.996 |
| Gas | Parameters | Search Range | Optimized Values | Integral Method [23] | Differential Method [23] |
|---|---|---|---|---|---|
| N2 | lnA [ln(s−1)] | [10.96,36.41] | 24.20 | 35.59 | 25.99 |
| Ea (kJ/mol) | [76.90,250.89] | 170.10 | 153.48 | 136.26 | |
| n | [−5,5] | 0.58 | 0.5 | 0.88 | |
| v | [0.05,0.95] | 0.05 | - | - | |
| Air | lnA [ln(s−1)] | [5.92,25.59] | 16.58 | 22.47 | 22.62 |
| Ea (kJ/mol) | [49.19,187.80] | 121.47 | 104.31 | 126.52 | |
| n | [−5,5] | 0.45 | 0.5 | 0.77 | |
| v | [0.05,0.95] | 0.16 | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, X.; Wu, Z.; Zhang, W.; Lu, K.; Ding, Y.; Mao, S. Energy Utilization of Building Insulation Waste Expanded Polystyrene: Pyrolysis Kinetic Estimation by a New Comprehensive Method. Polymers 2020, 12, 1744. https://doi.org/10.3390/polym12081744
Ni X, Wu Z, Zhang W, Lu K, Ding Y, Mao S. Energy Utilization of Building Insulation Waste Expanded Polystyrene: Pyrolysis Kinetic Estimation by a New Comprehensive Method. Polymers. 2020; 12(8):1744. https://doi.org/10.3390/polym12081744
Chicago/Turabian StyleNi, Xiaoyang, Zheng Wu, Wenlong Zhang, Kaihua Lu, Yanming Ding, and Shaohua Mao. 2020. "Energy Utilization of Building Insulation Waste Expanded Polystyrene: Pyrolysis Kinetic Estimation by a New Comprehensive Method" Polymers 12, no. 8: 1744. https://doi.org/10.3390/polym12081744
APA StyleNi, X., Wu, Z., Zhang, W., Lu, K., Ding, Y., & Mao, S. (2020). Energy Utilization of Building Insulation Waste Expanded Polystyrene: Pyrolysis Kinetic Estimation by a New Comprehensive Method. Polymers, 12(8), 1744. https://doi.org/10.3390/polym12081744