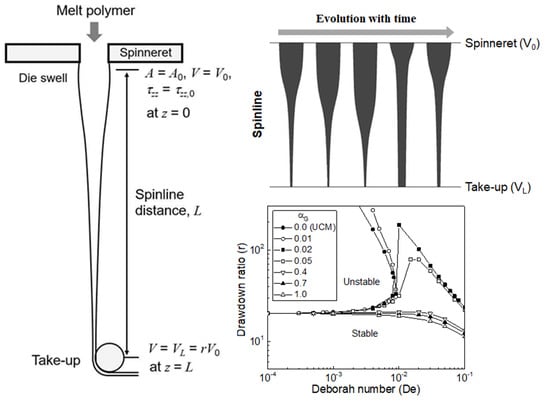
Effect of Material Parameter of Viscoelastic Giesekus Fluids on Extensional Properties in Spinline and Draw Resonance Instability in Isothermal Melt Spinning Process
Abstract
:1. Introduction
2. Simulation Methods
2.1. Governing Equations of Spinning Flows
2.2. Linear Stability Analysis of Steady Flows
2.3. Simple Stability Indicator Using Traveling Times of Kinematic Waves
3. Results and Discussion
3.1. Neutral Stability Curves with Respect to De for Giesekus Fluids with Different Values
3.2. Steady Extensional Properties of Giesekus Fluids in the Spinline
3.3. Transit Times of Kinematic Waves for Different Giesekus Fluids
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Denn, M.M. Continuous drawing of liquids to form fibers. Annu. Rev. Fluid Mech. 1980, 12, 365–387. [Google Scholar] [CrossRef]
- Christensen, R.E. Extrusion coating of polypropylene. SPE J. 1962, 18, 751–755. [Google Scholar]
- Miller, J.C. Swelling behavior in extrusion. Polym. Eng. Sci. 1963, 3, 134–137. [Google Scholar] [CrossRef]
- Jung, H.W.; Hyun, J.C. Instabilities in extensional deformation polymer processing. In Rheology Reviews, 2006; Binding, D.M., Walters, K., Eds.; The British Society of Rheology: Aberystwyth, UK, 2006; pp. 131–164. [Google Scholar]
- Jung, H.W.; Hyun, J.C. Fiber spinning and film blowing instabilities. In Polymer Processing Instabilities: Control and understanding, 1st ed.; Hatzikiriakos, S.G., Migler, K.B., Eds.; Marcel Dekker: New York, NY, USA, 2005; pp. 321–381. [Google Scholar]
- Gelder, D. The stability of fiber drawing processes. Ind. Eng. Chem. Fundam. 1971, 10, 534–535. [Google Scholar] [CrossRef]
- Fisher, R.J.; Denn, M.M. Finite-amplitude stability and draw resonance in isothermal melt spinning. Chem. Eng. Sci. 1975, 30, 1129–1134. [Google Scholar] [CrossRef]
- Jung, H.W.; Hyun, J.C. Stability of isothermal spinning of viscoelastic fluids. Korean J. Chem. Eng. 1999, 16, 325–330. [Google Scholar] [CrossRef]
- Götz, T.; Perera, S.S.N. Stability analysis of the melt spinning process with respect to parameters. ZAMM-Z. Angew. Math. Mech. 2009, 89, 874–880. [Google Scholar] [CrossRef]
- Bechert, M.; Scheid, B. Combined influence of inertia, gravity, and surface tension on the linear stability of Newtonian fiber spinning. Phys. Rev. Fluids 2017, 2, 1–19. [Google Scholar] [CrossRef]
- Kase, S.; Matsuo, T. Studies on melt spinning. II. Steady-state and transient solutions of fundamental equations compared with experimental results. J. Appl. Polym. Sci. 1967, 11, 251–287. [Google Scholar] [CrossRef]
- Hyun, J.C. Theory of draw resonance: Part I. Newtonian fluid & Part II Power-law and Maxwell fluids. AIChE J. 1978, 24, 418–426. [Google Scholar]
- Kim, B.M.; Hyun, J.C.; Oh, J.S.; Lee, S.J. Kinematic waves in the isothermal melt spinning of Newtonian fluids. AIChE J. 1996, 42, 3164–3169. [Google Scholar] [CrossRef]
- Jung, H.W.; Song, H.S.; Hyun, J.C. Draw resonance and kinematic waves in viscoelastic isothermal spinning. AIChE J. 2000, 46, 2106–2111. [Google Scholar] [CrossRef]
- Lee, J.S.; Jung, H.W.; Hyun, J.C.; Scriven, L.E. Simple indicator of draw resonance instability in melt spinning processes. AIChE J. 2005, 51, 2869–2874. [Google Scholar] [CrossRef]
- Schultz, W.W.; Zebib, A.; Davis, S.H.; Yee, L. Nonlinear stability of Newtonian fibres. J. Fluid Mech. 1984, 149, 455–475. [Google Scholar] [CrossRef] [Green Version]
- Yun, J.H.; Shin, D.M.; Lee, J.S.; Jung, H.W.; Hyun, J.C. Direct calculation of limit cycles of draw resonance and their stability in spinning process. Nihon Reoroji Gakkaishi. 2008, 36, 133–136. [Google Scholar] [CrossRef] [Green Version]
- Bergonzoni, A.; DiCresce, A.J. The phenomenon of draw resonance in polymeric melts. Part I—Qualitative view, Part II—Correlation to molecular parameters. Polym. Eng. Sci. 1966, 6, 45–59. [Google Scholar] [CrossRef]
- Demay, Y.; Agassant, J.F. Experimental study of draw resonance in fiber spinning. J. Non-Newton. Fluid Mech. 1985, 18, 187–198. [Google Scholar] [CrossRef]
- Kwon, I.; Chun, M.S.; Jung, H.W.; Hyun, J.C. Determination of draw resonance onsets in tension-controlled viscoelastic spinning process using transient frequency response method. J. Non-Newton. Fluid Mech. 2016, 228, 31–37. [Google Scholar] [CrossRef]
- Pearson, J.R.A.; Shah, Y.T. On the stability of isothermal and nonisothermal fiber spinning of power-law fluids. Ind. Eng. Chem. Fundam. 1974, 13, 134–138. [Google Scholar] [CrossRef]
- Lee, J.S.; Jung, H.W.; Kim, S.H.; Hyun, J.C. Effect of fluid viscoelasticity on the draw resonance dynamics of melt Spinning. J. Non-Newton. Fluid Mech. 2001, 99, 159–166. [Google Scholar] [CrossRef]
- Lee, J.S.; Jung, H.W.; Hyun, J.C. Melt spinning dynamics of Phan-Thien Tanner fluids. Korea-Aust. Rheol. J. 2000, 12, 119–124. [Google Scholar]
- Giesekus, H. A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J. Non-Newton. Fluid Mech. 1982, 11, 69–109. [Google Scholar] [CrossRef]
- Giesekus, H. A unified approach to a variety of constitutive models for polymer fluids based on the concept of configuration-dependent molecular mobility. Rheol. Acta. 1982, 11, 366–375. [Google Scholar] [CrossRef]
- Khan, S.A.; Larson, R.G. Comparison of simple constitutive equations for polymer melts in shear and biaxial and uniaxial extensions. J. Rheol. 1987, 31, 207–234. [Google Scholar] [CrossRef]
- Dhadwal, R. Numerical study of effect of inertia on stability of fibre spinning. Int. J. Appl. Comput. Math. 2016, 2, 699–711. [Google Scholar] [CrossRef] [Green Version]
- Iyengar, V.R.; Co, A. Film casting of a modified Giesekus fluid: Stability analysis. Chem. Eng. Sci. 1996, 51, 1417–1430. [Google Scholar] [CrossRef]
- Pis-Lopez, M.E.; Co, A. Multilayer film casting of modified Giesekus fluids Part2. Linear stability analysis. J. Non-Newton. Fluid Mech. 1996, 66, 95–114. [Google Scholar] [CrossRef]
- Doufas, A.K.; McHugh, A.J. Simulation of film blowing including flow-induced crystallization. J. Rheol. 2001, 45, 1085–1104. [Google Scholar] [CrossRef]
- Chang, J.C.; Denn, M.M. Sensitivity of the stability of isothermal melt spinning to rheological constitutive assumptions. In Rheology Vol 3: Application, 1st ed.; Astarita, G., Marrucci, G., Nicolais, L., Eds.; Plenum Press: New York, NY, USA, 1980; pp. 9–13. [Google Scholar]
- Papanastasiou, T.C.; Macosko, C.W.; Scriven, L.E. Fiber spinning of viscoelastic liquid. AIChE J. 1987, 33, 834–842. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, G.; Yun, J.; Lee, C.; Jung, H.W. Effect of Material Parameter of Viscoelastic Giesekus Fluids on Extensional Properties in Spinline and Draw Resonance Instability in Isothermal Melt Spinning Process. Polymers 2021, 13, 139. https://doi.org/10.3390/polym13010139
Park G, Yun J, Lee C, Jung HW. Effect of Material Parameter of Viscoelastic Giesekus Fluids on Extensional Properties in Spinline and Draw Resonance Instability in Isothermal Melt Spinning Process. Polymers. 2021; 13(1):139. https://doi.org/10.3390/polym13010139
Chicago/Turabian StylePark, Geunyeop, Jangho Yun, Changhoon Lee, and Hyun Wook Jung. 2021. "Effect of Material Parameter of Viscoelastic Giesekus Fluids on Extensional Properties in Spinline and Draw Resonance Instability in Isothermal Melt Spinning Process" Polymers 13, no. 1: 139. https://doi.org/10.3390/polym13010139
APA StylePark, G., Yun, J., Lee, C., & Jung, H. W. (2021). Effect of Material Parameter of Viscoelastic Giesekus Fluids on Extensional Properties in Spinline and Draw Resonance Instability in Isothermal Melt Spinning Process. Polymers, 13(1), 139. https://doi.org/10.3390/polym13010139