Wave Dispersion Analysis of Fluid Conveying Nanocomposite Shell Reinforced by MWCNTs Considering the Effect of Waviness and Agglomeration Efficiency
Abstract
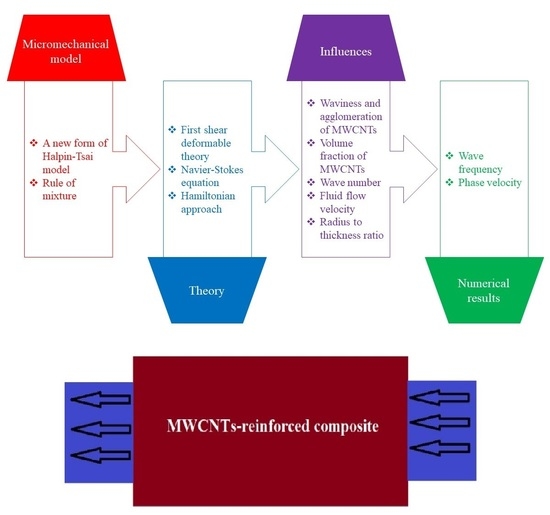
:1. Introduction
2. Theory and Formulation
2.1. Homogenization Procedure
2.2. Kinetic Relations
3. Analytical Solution Scheme
4. Numerical Results and Discussion
5. Conclusions
- The phase velocity and wave frequency of the fluid-conveying MWCNT-reinforced nanocomposite cylindrical shell decreased with enhancing the fluid flow velocity.
- An increment in the radius to thickness ratio declined the phase velocity and wave frequency of the fluid-conveying MWCNT-reinforced nanocomposite cylindrical shells.
- Agglomeration and waviness factor affected the mechanical behavior of nanocomposite shells in a decreasing manner.
- Regardless of the agglomeration factor, an enhancement in the MWCNT content augmented the elastic modulus, wave frequency, and phase velocity.
- The increment of parameter α plays a decreasing role in the variation of phase velocity.
- Resolving the MWCNTs agglomeration is vital to enhance the mechanical behavior of nanocomposite cylindrical shells.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Kollar, L.P.; Springer, G.S. Mechanics of Composite Structures; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kant, T.; Swaminathan, K. Analytical solutions for free vibration of laminated composite and sandwich plates based on a higher-order refined theory. Compos. Struct. 2001, 53, 73–85. [Google Scholar] [CrossRef]
- Tripathi, V.; Singh, B.; Shukla, K. Free vibration of laminated composite conical shells with random material properties. Compos. Struct. 2007, 81, 96–104. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. Free vibration of laminated composite plates using two variable refined plate theory. Int. J. Mech. Sci. 2010, 52, 626–633. [Google Scholar] [CrossRef]
- Houmat, A. Nonlinear free vibration of laminated composite rectangular plates with curvilinear fibers. Compos. Struct. 2013, 106, 211–224. [Google Scholar] [CrossRef]
- Verma, K.L. Wave propagation in laminated composite plates. Int. J. Adv. Struct. Eng. 2013, 5, 10. [Google Scholar] [CrossRef] [Green Version]
- Panda, S.K.; Singh, B. Nonlinear finite element analysis of thermal post-buckling vibration of laminated composite shell panel embedded with SMA fibre. Aerosp. Sci. Technol. 2013, 29, 47–57. [Google Scholar] [CrossRef]
- Kumar, A.; Chakrabarti, A.; Bhargava, P. Vibration of laminated composites and sandwich shells based on higher order zigzag theory. Eng. Struct. 2013, 56, 880–888. [Google Scholar] [CrossRef]
- Nedri, K.; El Meiche, N.; Tounsi, A. Free vibration analysis of laminated composite plates resting on elastic foundations by using a refined hyperbolic shear deformation theory. Mech. Compos. Mater. 2014, 49, 629–640. [Google Scholar] [CrossRef]
- Panda, S.K.; Katariya, P.V. Stability and free vibration behaviour of laminated composite panels under thermo-mechanical loading. Int. J. Appl. Comput. Math. 2015, 1, 475–490. [Google Scholar] [CrossRef] [Green Version]
- Dey, T.; Ramachandra, L. Non-linear vibration analysis of laminated composite circular cylindrical shells. Compos. Struct. 2017, 163, 89–100. [Google Scholar] [CrossRef]
- Barouni, A.K.; Saravanos, D.A. A layerwise semi-analytical method for modeling guided wave propagation in laminated composite infinite plates with induced surface excitation. Wave Motion 2017, 68, 56–77. [Google Scholar] [CrossRef]
- Chaubey, A.K.; Kumar, A.; Chakrabarti, A. Vibration of laminated composite shells with cutouts and concentrated mass. AIAA J. 2018, 56, 1662–1678. [Google Scholar] [CrossRef]
- Gao, J.; Lyu, Y.; Zheng, M.; Liu, M.; Liu, H.; Wu, B.; He, C. Modeling guided wave propagation in multi-layered anisotropic composite laminates by state-vector formalism and the Legendre polynomials. Compos. Struct. 2019, 228, 111319. [Google Scholar] [CrossRef]
- Nastos, C.; Saravanos, D. A finite wavelet domain method for wave propagation analysis in thick laminated composite and sandwich plates. Wave Motion 2020, 102543. [Google Scholar] [CrossRef]
- Safaei, B. The effect of embedding a porous core on the free vibration behavior of laminated composite plates. Steel Compos. Struct. 2020, 35, 659–670. [Google Scholar]
- Shen, H.-S.; Xiang, Y. Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput. Methods Appl. Mech. Eng. 2012, 213, 196–205. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M. Axial postbuckling analysis of multilayer functionally graded composite nanoplates reinforced with GPLs based on nonlocal strain gradient theory. Eur. Phys. J. Plus 2017, 132, 1–17. [Google Scholar] [CrossRef]
- Sahmani, S.; Fattahi, A.M.; Ahmed, N. Analytical mathematical solution for vibrational response of postbuckled laminated FG-GPLRC nonlocal strain gradient micro-/nanobeams. Eng. Comput. 2019, 35, 1173–1189. [Google Scholar] [CrossRef]
- Mirjavadi, S.S.; Forsat, M.; Barati, M.R.; Hamouda, A. Post-buckling analysis of geometrically imperfect tapered curved micro-panels made of graphene oxide powder reinforced composite. Steel Compos. Struct. 2020, 36, 63–74. [Google Scholar]
- Mirjavadi, S.S.; Forsat, M.; Mollaee, S.; Barati, M.R.; Afshari, B.M.; Hamouda, A. Post-buckling analysis of geometrically imperfect nanoparticle reinforced annular sector plates under radial compression. Comput. Concr. 2020, 26, 21–30. [Google Scholar]
- Heshmati, M.; Yas, M. Vibrations of non-uniform functionally graded MWCNTs-polystyrene nanocomposite beams under action of moving load. Mater. Des. 2013, 46, 206–218. [Google Scholar] [CrossRef]
- Kiani, Y. Free vibration of FG-CNT reinforced composite spherical shell panels using Gram-Schmidt shape functions. Compos. Struct. 2017, 159, 368–381. [Google Scholar] [CrossRef]
- Wang, A.; Chen, H.; Hao, Y.; Zhang, W. Vibration and bending behavior of functionally graded nanocomposite doubly-curved shallow shells reinforced by graphene nanoplatelets. Results Phys. 2018, 9, 550–559. [Google Scholar] [CrossRef]
- Liu, D.; Kitipornchai, S.; Chen, W.; Yang, J. Three-dimensional buckling and free vibration analyses of initially stressed functionally graded graphene reinforced composite cylindrical shell. Compos. Struct. 2018, 189, 560–569. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Srinivas, J. Transient vibration analysis of FG-MWCNT reinforced composite plate resting on foundation. Steel Compos. Struct. 2018, 29, 569–578. [Google Scholar]
- Ebrahimi, F.; Seyfi, A.; Dabbagh, A.; Tornabene, F. Wave dispersion characteristics of porous graphene platelet-reinforced composite shells. Struct. Eng. Mech. 2019, 71, 99–107. [Google Scholar]
- Karami, B.; Shahsavari, D.; Janghorban, M.; Li, L. Elastic guided waves in fully-clamped functionally graded carbon nanotube-reinforced composite plates. Mater. Res. Express 2019, 6, 0950a0959. [Google Scholar] [CrossRef]
- Qaderi, S.; Ebrahimi, F.; Seyfi, A. An investigation of the vibration of multi-layer composite beams reinforced by graphene platelets resting on two parameter viscoelastic foundation. SN Appl. Sci. 2019, 1, 399. [Google Scholar] [CrossRef] [Green Version]
- Ghassabi, M.; Zarastvand, M.; Talebitooti, R. Investigation of state vector computational solution on modeling of wave propagation through functionally graded nanocomposite doubly curved thick structures. Eng. Comput. 2019, 36, 1417–1433. [Google Scholar] [CrossRef]
- Barati, M.R.; Zenkour, A.M. Vibration analysis of functionally graded graphene platelet reinforced cylindrical shells with different porosity distributions. Mech. Adv. Mater. Struct. 2019, 26, 1580–1588. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Nouraei, M.; Dabbagh, A. Thermal vibration analysis of embedded graphene oxide powder-reinforced nanocomposite plates. Eng. Comput. 2019, 36, 879–895. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Nouraei, M.; Dabbagh, A.; Rabczuk, T. Thermal buckling analysis of embedded graphene-oxide powder-reinforced nanocomposite plates. Adv. Nano Res. 2019, 7, 293–310. [Google Scholar]
- Lal, A.; Markad, K. Thermo-mechanical post buckling analysis of multiwall carbon nanotube-reinforced composite laminated beam under elastic foundation. Curved Layer. Struct. 2019, 6, 212–228. [Google Scholar] [CrossRef]
- Lee, S.-Y. Dynamic stability and nonlinear transient behaviors of CNT-reinforced fiber/polymer composite cylindrical panels with delamination around a cutout. Nonlinear Dyn. 2020, 25, 2551–2569. [Google Scholar] [CrossRef]
- Jam, J.; Pourasghar, A.; Kamarian, S. Effect of the aspect ratio and waviness of carbon nanotubes on the vibrational behavior of functionally graded nanocomposite cylindrical panels. Polym. Compos. 2012, 33, 2036–2044. [Google Scholar] [CrossRef]
- Rashidifar, M.A.; Ahmadi, D. Vibration analysis of randomly oriented carbon nanotube based on FGM beam using Timoshenko theory. Adv. Mech. Eng. 2015, 7, 653950. [Google Scholar] [CrossRef] [Green Version]
- Sepahvand, K. Spectral stochastic finite element vibration analysis of fiber-reinforced composites with random fiber orientation. Compos. Struct. 2016, 145, 119–128. [Google Scholar] [CrossRef]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis of conical shells reinforced with agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108, 157–165. [Google Scholar] [CrossRef]
- Tahouneh, V. Effects of CNTs waviness and aspect ratio on vibrational response of FG-sector plate. Steel Compos. Struct. 2017, 25, 649–661. [Google Scholar]
- García-Macías, E.; Castro-Triguero, R. Coupled effect of CNT waviness and agglomeration: A case study of vibrational analysis of CNT/polymer skew plates. Compos. Struct. 2018, 193, 87–102. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Seyfi, A.; Dabbagh, A. Wave dispersion characteristics of agglomerated multi-scale hybrid nanocomposite beams. J. Strain Anal. Eng. Des. 2019, 54, 276–289. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Seyfi, A. Wave propagation response of multi-scale hybrid nanocomposite shell by considering aggregation effect of CNTs. Mech. Based Des. Struct. Mach. 2019, 1–22. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Seyfi, A. Wave propagation response of agglomerated multi-scale hybrid nanocomposite plates. Waves Random Complex Media 2020, 1–25. [Google Scholar] [CrossRef]
- Chung, K.L.; Luo, J.; Yuan, L.; Zhang, C.; Qu, C. Strength correlation and prediction of engineered cementitious composites with microwave properties. Appl. Sci. 2017, 7, 35. [Google Scholar] [CrossRef] [Green Version]
- Chung, K.L.; Zhang, C.; Li, Y.; Sun, L.; Ghannam, M. Microwave non-destructive inspection and prediction of modulus of rupture and modulus of elasticity of engineered cementitious composites (ECCs) using dual-frequency correlation. Sensors 2017, 17, 2831. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chung, K.L.; Zhang, C. Flexural Strength Estimation of Engineered Cementitious Composites by Using Microwave NDT. In Proceedings of the 2018 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Nagoya, Japan, 29–31 August 2018; pp. 1–2. [Google Scholar]
- Hassanzadeh-Aghdam, M.K.; Jamali, J. A new form of a Halpin–Tsai micromechanical model for characterizing the mechanical properties of carbon nanotube-reinforced polymer nanocomposites. Bull. Mater. Sci. 2019, 42, 117. [Google Scholar] [CrossRef] [Green Version]
- Cox, H. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
- Rabani Bidgoli, M.; Saeed Karimi, M.; Ghorbanpour Arani, A. Nonlinear vibration and instability analysis of functionally graded CNT-reinforced cylindrical shells conveying viscous fluid resting on orthotropic Pasternak medium. Mech. Adv. Mater. Struct. 2016, 23, 819–831. [Google Scholar] [CrossRef]
- Pradhan, S.; Loy, C.; Lam, K.; Reddy, J. Vibration characteristics of functionally graded cylindrical shells under various boundary conditions. Appl. Acoust. 2000, 61, 111–129. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D. Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 2017, 66, 83–91. [Google Scholar] [CrossRef]
- Li, H.; Pang, F.; Chen, H.; Du, Y. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Compos. Part B Eng. 2019, 164, 249–264. [Google Scholar] [CrossRef]









| Mechanical Properties | Polystyrene [22] | MWCNT [48] |
|---|---|---|
| E (GPa) | 1.9 | 800 |
| ρ (Kg/m3) | 1050 | 2100 |
| υ | 0.34 | 0.28 |
| n | Pradhan, Loy, Lam and Reddy [51] | Error (%) | Wang and Wu [52] | Error (%) | Li, Pang, Chen and Du [53] | Error (%) | Present |
|---|---|---|---|---|---|---|---|
| 1 | 0.0342 | 2.632 | 0.0340 | 3.235 | 0.0332 | 5.723 | 0.0351 |
| 2 | 0.0119 | 2.521 | 0.0119 | 2.521 | 0.0117 | 4.274 | 0.0122 |
| 3 | 0.0072 | 0 | 0.0072 | 0 | 0.0071 | 1.389 | 0.0072 |
| 4 | 0.0089 | 0 | 0.0090 | 1.124 | 0.0090 | 1.124 | 0.0089 |
| 5 | 0.0136 | 0.735 | 0.0137 | 1.460 | 0.0137 | 1.460 | 0.0135 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhedher, M.; Talebizadehsardari, P.; Eyvazian, A.; Khan, A.; Farouk, N. Wave Dispersion Analysis of Fluid Conveying Nanocomposite Shell Reinforced by MWCNTs Considering the Effect of Waviness and Agglomeration Efficiency. Polymers 2021, 13, 153. https://doi.org/10.3390/polym13010153
Alkhedher M, Talebizadehsardari P, Eyvazian A, Khan A, Farouk N. Wave Dispersion Analysis of Fluid Conveying Nanocomposite Shell Reinforced by MWCNTs Considering the Effect of Waviness and Agglomeration Efficiency. Polymers. 2021; 13(1):153. https://doi.org/10.3390/polym13010153
Chicago/Turabian StyleAlkhedher, Mohammad, Pouyan Talebizadehsardari, Arameh Eyvazian, Afrasyab Khan, and Naeim Farouk. 2021. "Wave Dispersion Analysis of Fluid Conveying Nanocomposite Shell Reinforced by MWCNTs Considering the Effect of Waviness and Agglomeration Efficiency" Polymers 13, no. 1: 153. https://doi.org/10.3390/polym13010153
APA StyleAlkhedher, M., Talebizadehsardari, P., Eyvazian, A., Khan, A., & Farouk, N. (2021). Wave Dispersion Analysis of Fluid Conveying Nanocomposite Shell Reinforced by MWCNTs Considering the Effect of Waviness and Agglomeration Efficiency. Polymers, 13(1), 153. https://doi.org/10.3390/polym13010153