The Self-Enforcing Starch–Gluten System—Strain–Dependent Effects of Yeast Metabolites on the Polymeric Matrix
Abstract
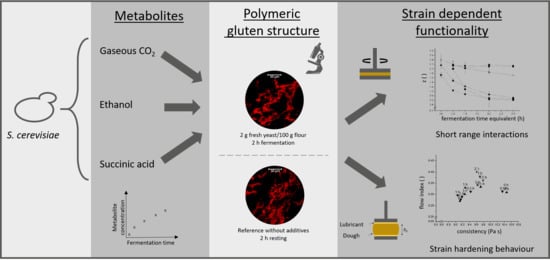
:1. Introduction
2. Materials and Methods
2.1. Wheat Dough Composition
2.2. Fundamental Shear Rheology
2.3. Elongation Properties by Lubricated Squeezing Flow
2.4. Microstructural Analysis
2.5. Statistical Analysis
3. Results
3.1. Network Characterisation under Small Deformation
3.2. Extensional Viscosity of Yeasted Wheat Dough
3.3. Linkage between Extensional Rheological Properties and Protein Network Configuration
3.4. Strain Hardening Behaviour of Yeasted Wheat Dough
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rouillé, J.; Della Valle, G.; Lefebvre, J.; Sliwinski, E.; VanVliet, T. Shear and extensional properties of bread doughs affected by their minor components. J. Cereal Sci. 2005, 42, 45–57. [Google Scholar] [CrossRef]
- Schiedt, B.; Baumann, A.; Conde-Petit, B.; Vilgis, T.A. Short- and long-range interactions governing the viscoelastic properties during wheat dough and model dough development. J. Texture Stud. 2013, 44, 317–332. [Google Scholar] [CrossRef]
- Bloksma, A.H. Dough structure, dough rheology and baking quality. Cereal Foods World 1990, 35, 237–244. [Google Scholar]
- Van Vliet, T.; Janssen, A.M.; Bloksma, A.H.; Walstra, P. Strain hardening of dough as a requirement for gas retention. J. Texture Stud. 1992, 23, 439–460. [Google Scholar] [CrossRef]
- Weegels, P.L.; Groeneweg, F.; Esselink, E.; Smit, R.; Brown, R.; Ferdinando, D. Large and fast deformations crucial for the rheology of proofing dough. Cereal Chem. 2003, 80, 424–426. [Google Scholar] [CrossRef]
- Wikström, K.; Bohlin, L. Extensional flow studies of wheat flour dough. I. Experimental method for measurement in contraction flow geometry and application to flours varying in breadmaking performance. J. Cereal Sci. 1999, 29, 217–226. [Google Scholar] [CrossRef]
- Aslankoohi, E.; Rezaei, M.N.; Vervoort, Y.; Courtin, C.M.; Verstrepen, K.J. Glycerol production by fermenting yeast cells is essential for optimal bread dough fermentation. PLoS ONE 2015, 10, 1–13. [Google Scholar] [CrossRef]
- Jayaram, V.B.; Cuyvers, S.; Verstrepen, K.J.; Delcour, J.A.; Courtin, C.M. Succinic acid in levels produced by yeast (Saccharomyces cerevisiae) during fermentation strongly impacts wheat bread dough properties. Food Chem. 2014, 151, 421–428. [Google Scholar] [CrossRef]
- Jayaram, V.B.; Rezaei, M.N.; Cuyvers, S.; Verstrepen, K.J.; Delcour, J.A.; Courtin, C.M. Ethanol at levels produced by Saccharomyces cerevisiae during wheat dough fermentation has a strong impact on dough properties. J. Agric. Food Chem. 2014, 62, 9326–9335. [Google Scholar] [CrossRef]
- Meerts, M.; Ramirez Cervera, A.; Struyf, N.; Cardinaels, R.; Courtin, C.M.; Moldenaers, P. The effects of yeast metabolites on the rheological behaviour of the dough matrix in fermented wheat flour dough. J. Cereal Sci. 2018, 82, 183–189. [Google Scholar] [CrossRef] [Green Version]
- Meerts, M.; Vaes, D.; Botteldoorn, S.; Courtin, C.M.; Cardinaels, R.; Moldenaers, P. The time-dependent rheology of fermenting wheat flour dough: Effects of salt and sugar. Rheol. Acta 2018, 57, 813–827. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, M.N.; Jayaram, V.B.; Verstrepen, K.J.; Courtin, C.M. The impact of yeast fermentation on dough matrix properties. J. Sci. Food Agric. 2016, 96, 3741–3748. [Google Scholar] [CrossRef] [PubMed]
- Verheyen, C.; Albrecht, A.; Becker, T.; Jekle, M. Destabilization of wheat dough: Interrelation between CO2 and glutathione. Innov. Food Sci. Emerg. Technol. 2016, 34, 320–325. [Google Scholar] [CrossRef]
- Tronsmo, K.M.; Magnus, E.M.; Baardseth, P.; Schofield, J.D.; Aamodt, A.; Færgestad, E.M. Comparison of small and large deformation rheological properties of wheat dough and gluten. Cereal Chem. 2003, 80, 587–595. [Google Scholar] [CrossRef]
- Lucas, I.; Petermeier, H.; Becker, T.; Jekle, M. Definition of network types—Prediction of dough mechanical behaviour under shear by gluten microstructure. Sci. Rep. 2019, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Jayaram, V.B.; Cuyvers, S.; Lagrain, B.; Verstrepen, K.J.; Delcour, J.A.; Courtin, C.M. Mapping of saccharomyces cerevisiae metabolites in fermenting wheat straight-dough reveals succinic acid as pH-determining factor. Food Chem. 2013, 136, 301–308. [Google Scholar] [CrossRef] [PubMed]
- Gabriele, D.; de Cindio, B.; D’Antona, P. A weak gel model for foods. Rheol. Acta 2001, 40, 120–127. [Google Scholar] [CrossRef]
- Chatraei, S.; Macosko, C.W.; Winter, H.H. Lubricated squeezing flow: A new biaxial extensional rheometer. J. Rheol. 1981, 25, 433–443. [Google Scholar] [CrossRef]
- Kokelaar, J.J.; Van Vliet, T.; Prins, A. Strain hardening properties and extensibility of flour and gluten doughs in relation to breadmaking performance. J. Cereal Sci. 1996, 24, 199–214. [Google Scholar] [CrossRef]
- Lucas, I.; Stauner, B.; Jekle, M.; Becker, T. Staining methods for dough systems—Impact on microstructure and functionality. LWT 2018, 88, 139–145. [Google Scholar] [CrossRef]
- Bernklau, I.; Lucas, L.; Jekle, M.; Becker, T. Protein network analysis—A new approach for quantifying wheat dough microstructure. Food Res. Int. 2016, 89, 812–819. [Google Scholar] [CrossRef] [PubMed]
- Zudaire, E.; Gambardella, L.; Kurcz, C.; Vermeren, S. A computational tool for quantitative analysis of vascular networks. PLoS ONE 2011, 6, e27385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hering, E.; Martin, R.; Stohrer, M. Fehlerrechnung. In Taschenbuch der Mathematik und Physik2; Springer: Berlin, Germany, 2017; p. 114. [Google Scholar]
- Belton, P.S. Mini review: On the elasticity of wheat gluten. J. Cereal Sci. 1999, 29, 103–107. [Google Scholar] [CrossRef]
- Kawamura, Y.; Yonezawa, D. Wheat flour proteases and their action on gluten proteins in dilute acetic acid. Agric. Biol. Chem. 1982, 46, 767–773. [Google Scholar] [CrossRef]
- Dobraszczyk, B.J. The physics of baking: Rheological and polymer molecular structure-function relationships in breadmaking. J. Non-Newton. Fluid Mech. 2004, 124, 61–69. [Google Scholar] [CrossRef]
- Chin, N.L.; Martin, P.J.; Campbell, G.M. Dough aeration and rheology: Part 3. Effect of the presence of gas bubbles in bread dough on measured bulk rheology and work input rate. J. Sci. Food Agric. 2005, 85, 2203–2212. [Google Scholar] [CrossRef]
- Robertson, G.H.; Cao, T.K.; Ong, I. Wheat gluten swelling and partial solubility with potential impact on starch-from-gluten separation by ethanol washing. Cereal Chem. 1999, 76, 843–845. [Google Scholar] [CrossRef]
- Wehrle, K.; Grau, H.; Arendt, E.K. Effects of lactic acid, acetic acid, and table salt on fundamental rheological properties of wheat dough. Cereal Chem. 1997, 74, 739–744. [Google Scholar] [CrossRef]
- Barnes, H.A.; Hutton, J.F.; Walters, K. Rheology of polymeric liquids. In An introduction to Rheology; Elsevier: Amsterdam, The Netherlands, 1989; pp. 97–114. [Google Scholar]
- Turbin-Orger, A.; Boller, E.; Chaunier, L.; Chiron, H.; Della Valle, G.; Réguerre, A.L. Kinetics of bubble growth in wheat flour dough during proofing studied by computed X-ray micro-tomography. J. Cereal Sci. 2012, 56, 676–683. [Google Scholar] [CrossRef]
- Weipert, D. The benefits of basic rheometry in studying dough rheology. Cereal Chem. 1990, 67, 311–317. [Google Scholar]
- Lyu, M.-Y.; Lee, J.S.; Youlee, P. Study of mechanical and rheological behaviors of linear and branched polycarbonates blends. J. Appl. Polym. Sci. 2001, 80, 1814–1824. [Google Scholar] [CrossRef]
- Dealy, J.M.; Read, D.J.; Larson, R.G. Structure and Rheology of Molten Polymers: From Structure to Flow Behavior and Back Again; Carl Hanser: Munich, Germany, 2018. [Google Scholar]
- Singh, H.; Macritchie, F. Application of polymer science to properties of gluten. J. Cereal Sci. 2001, 33, 231–243. [Google Scholar] [CrossRef]
- Mccann, T.H.; Le Gall, M.; Day, L. Extensional dough rheology—Impact of flour composition and extension speed. J. Cereal Sci. 2016, 69, 228–237. [Google Scholar] [CrossRef]
- Jongen, T.R.G.; Bruschke, M.V.; Dekker, J.G. Analysis of dough kneaders using numerical flow simulations. Cereal Chem. 2003, 80, 383–389. [Google Scholar] [CrossRef]
- Turbin-Orger, A.; Shehzad, A.; Chaunier, L.; Chiron, H.; Della Valle, G. Elongational properties and proofing behaviour of wheat flour dough. J. Food Eng. 2016, 168, 129–136. [Google Scholar] [CrossRef]
- Jekle, M.; Becker, T. Wheat dough microstructure: The relation between visual structure and mechanical behavior. Crit. Rev. Food Sci. Nutr. 2015, 55, 369–382. [Google Scholar] [CrossRef]
- Janssen, A.M.; Van Vliet, T.; Vereijken, J.M. Fundamental and empirical rheological behaviour of wheat flour doughs and comparison with bread making performance. J. Cereal Sci. 1996, 23, 43–54. [Google Scholar] [CrossRef]
- Belton, P.S. New approaches to study the molecular basis of the mechanical properties of gluten. J. Cereal Sci. 2005, 41, 203–211. [Google Scholar] [CrossRef]
- Babin, P.; Della Valle, G.; Chiron, H.; Cloetens, P.; Hoszowska, J.; Pernot, P.; Réguerre, A.L.; Salvo, L.; Dendievel, R. In situ fast x-ray tomography study of the evaluation of cellular structure in bread dough during proving and baking. In Bubbles in Food 2: Novelty, Health and Luxury; Campbell, G.M., Scanlon, M.G., Pyle, D.L., Eds.; American Association of Cereal Chemists International: St. Paul, MN, USA, 2016; pp. 265–272. ISBN 9780128104590. [Google Scholar]





| Average Protein Vessel Length (µm) | Average Lacunarity (-) | Branching Rate (Junctions/µm2) | Endpoint Rate (End Points/µm2) | Protein Width (µm) | |
|---|---|---|---|---|---|
| Standard wheat dough without additives 0 h resting | 7217 ± 2586 a | 0.35 ± 0.04 a | 6.1·10−5 ± 0.4·10−5 a | 1.6·10−5 ± 0.2·10−5 a | 69.53 ± 1.54 a |
| Standard wheat dough without additives 2 h resting | 5298 ± 1307 a | 0.35 ± 0.06 a | 5.8·10−5 ± 0.5·10−5 a | 2.1·10−5 ± 0.3·10−5 b | 66.07 ± 0.66 b |
| 2 g yeast/100 g flour 2 h fermentation | 4503 ± 1511 b | 0.41 ± 0.12 a | 5.6·10−5 ± 0.4·10−5 b | 2.2·10−5 ± 0.4·10−5 b | 66.95 ± 1.81 b |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alpers, T.; Tauscher, V.; Steglich, T.; Becker, T.; Jekle, M. The Self-Enforcing Starch–Gluten System—Strain–Dependent Effects of Yeast Metabolites on the Polymeric Matrix. Polymers 2021, 13, 30. https://doi.org/10.3390/polym13010030
Alpers T, Tauscher V, Steglich T, Becker T, Jekle M. The Self-Enforcing Starch–Gluten System—Strain–Dependent Effects of Yeast Metabolites on the Polymeric Matrix. Polymers. 2021; 13(1):30. https://doi.org/10.3390/polym13010030
Chicago/Turabian StyleAlpers, Thekla, Viviane Tauscher, Thomas Steglich, Thomas Becker, and Mario Jekle. 2021. "The Self-Enforcing Starch–Gluten System—Strain–Dependent Effects of Yeast Metabolites on the Polymeric Matrix" Polymers 13, no. 1: 30. https://doi.org/10.3390/polym13010030
APA StyleAlpers, T., Tauscher, V., Steglich, T., Becker, T., & Jekle, M. (2021). The Self-Enforcing Starch–Gluten System—Strain–Dependent Effects of Yeast Metabolites on the Polymeric Matrix. Polymers, 13(1), 30. https://doi.org/10.3390/polym13010030