Actuator Behaviour of Tailored Poly(thiourethane) Shape Memory Thermosets
Abstract
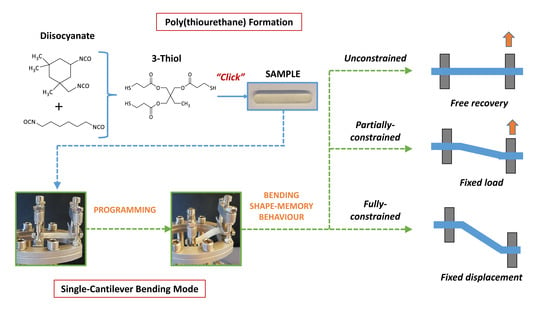
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Reparation
2.3. Rheological Characterization
2.4. Thermal Characterization
2.5. Thermo-Mechanical Characterization
2.6. Mechanical Characterization
2.7. Shape Memory Characterization
3. Results
3.1. Rheological Study
3.2. Thermal Degradation Study
3.3. Thermomechanical Analysis
3.4. Shape-Memory Results
3.4.1. Unconstrained Recovery
3.4.2. Fully-Constrained Recovery Tests
3.5. Partially-Constrained Recovery Tests
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hager, M.D.; Bode, S.; Weber, C.; Schubert, U.S. Shape memory polymers: Past, present and future developments. Prog. Polym. Sci. 2015, 49–50, 3–33. [Google Scholar] [CrossRef]
- Zhao, Q.; Qi, H.J.; Xie, T. Recent progress in shape memory polymer: New behavior, enabling materials, and mechanistic understanding. Prog. Polym. Sci. 2015, 49–50, 79–120. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Zhu, Y.; Huang, H.; Lu, J. Recent advances in shape–memory polymers: Structure, mechanism, functionality, modelling and applications. Prog. Polym. Sci. 2012, 37, 1720–1763. [Google Scholar] [CrossRef]
- Souri, M.; Lu, Y.; Erol, A.; Pulla, S.; Karaca, H. Characterization of unconstraint and constraint shape recoveries of an epoxy based shape memory polymer. Polym. Test. 2015, 41, 231–238. [Google Scholar] [CrossRef]
- Lendlein, A.; Gould, O.E.C. Reprogrammable recovery and actuation behaviour of shape-memory polymers. Nat. Rev. Mater. 2019, 4, 116–133. [Google Scholar] [CrossRef]
- Berg, G.J.; McBride, M.K.; Wang, C.; Bowman, C.N. New directions in the chemistry of shape memory polymers. Polymer 2014, 55, 5849–5872. [Google Scholar] [CrossRef]
- Anthamatten, M.; Roddecha, S.; Li, J. Energy Storage Capacity of Shape-Memory Polymers. Macromolecules 2013, 46, 4230–4234. [Google Scholar] [CrossRef]
- Belmonte, A.; Guzmán, D.; Fernández-Francos, X.; De la Flor, S. Effect of the network structure and programming temperature on the shape-memory response of thiol-epoxy “click” systems. Polymers 2015, 7, 2146–2164. [Google Scholar] [CrossRef]
- Liu, R.; Xu, S.; Luo, X.; Liu, Z. Theoretical and Numerical Analysis of Mechanical Behaviors of a Metamaterial-Based Shape Memory Polymer Stent. Polymers 2020, 12, 1784. [Google Scholar] [CrossRef] [PubMed]
- Hardy, J.G.; Palma, M.; Wind, S.J.; Biggs, M.J. Responsive Biomaterials: Advances in Materials Based on Shape-Memory Polymers. Adv. Mater. 2016, 28, 5717–5724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Du, H.; Liu, L.; Leng, J. Shape memory polymers and their composites in aerospace applications: A review. Smart Mater. Struct. 2014, 23, 023001. [Google Scholar] [CrossRef]
- Hu, J.; Chen, S. A review of actively moving polymers in textile applications. J. Mater. Chem. 2010, 20, 3346–3355. [Google Scholar] [CrossRef]
- Pilate, F.; Toncheva, A.; Dubois, P.; Raquez, J.-M. Shape-memory polymers for multiple applications in the materials world. Eur. Polym. J. 2016, 80, 268–294. [Google Scholar] [CrossRef]
- Xie, F.; Huang, L.; Leng, J.; Liu, Y. Thermoset shape memory polymers and their composites. J. Intell. Mater. Syst. Struct. 2016, 27, 2433–2455. [Google Scholar] [CrossRef]
- Belmonte, A.; Fernández-Francos, X.; De la Flor, S. New understanding of the shape-memory response in thiol-epoxy click systems: Towards controlling the recovery process. J. Mater. Sci. 2017, 52, 1625–1638. [Google Scholar] [CrossRef] [Green Version]
- Karger-Kocsis, J.; Kéki, S. Review of Progress in Shape Memory Epoxies and Their Composites. Polymers 2017, 10, 34. [Google Scholar] [CrossRef] [Green Version]
- Russo, C.; Fernández Francos, X.; De la Flor, S. Shape-memory actuators based on dual-curing thiol-acrylate-epoxy thermosets. Express Polym. Lett. 2020, 15, 58–71. [Google Scholar] [CrossRef]
- Belmonte, A.; Fernández-Francos, X.; De la Flor, S. Thermomechanical characterization of thiol-epoxy shape memory thermosets for mechanical actuators design. AIP Conf. Proc. 2018, 030012, 1–12. [Google Scholar]
- Santiago, D.; Fabregat-Sanjuan, A.; Ferrando, F.; De La Flor, S. Recovery stress and work output in hyperbranched poly(ethyleneimine)-modified shape-memory epoxy polymers. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1002–1013. [Google Scholar] [CrossRef]
- Belmonte, A.; Lama, G.C.; Gentile, G.; Cerruti, P.; Ambrogi, V.; Fernández-Francos, X.; De La Flor, S. Thermally-triggered free-standing shape-memory actuators. Eur. Polym. J. 2017, 97, 241–252. [Google Scholar] [CrossRef]
- Belmonte, A.; Russo, C.; Ambrogi, V.; Fernández-Francos, X.; De la Flor, S. Epoxy-based shape-memory actuators obtained via dual-curing of off-stoichiometric “thiol-epoxy” mixtures. Polymers 2017, 9, 113. [Google Scholar] [CrossRef] [Green Version]
- Jahid, M.A.; Hu, J.; Wong, K.; Wu, Y.; Zhu, Y.; Sheng Luo, H.H.; Zhongmin, D. Fabric Coated with Shape Memory Polyurethane and Its Properties. Polymers 2018, 10, 681. [Google Scholar] [CrossRef] [Green Version]
- Kausar, A. Review on Technological Significance of Photoactive, Electroactive, pH-sensitive, Water-active, and Thermoresponsive Polyurethane Materials. Polym. Plast. Technol. Eng. 2017, 56, 606–616. [Google Scholar] [CrossRef]
- Song, X.; Chi, H.; Li, Z.; Li, T.; Wang, F. Star-Shaped Crosslinker for Multifunctional Shape Memory Polyurethane. Polymers 2020, 12, 740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delebecq, E.; Pascault, J.-P.; Boutevin, B.; Ganachaud, F. On the Versatility of Urethane/Urea Bonds: Reversibility, Blocked Isocyanate, and Non-isocyanate Polyurethane. Chem. Rev. 2013, 113, 80–118. [Google Scholar] [CrossRef]
- Ireni, N.G.; Narayan, R.; Basak, P.; Raju, K.V.S.N. Poly(thiourethane-urethane-urea) as anticorrosion coatings with impressive optical properties. Polymer 2016, 97, 370–379. [Google Scholar] [CrossRef]
- Li, C.; Tan, J.; Li, H.; Yin, D.; Gu, J.; Zhang, B.; Zhang, Q. Thiol–isocyanate click reaction in a Pickering emulsion: A rapid and efficient route to encapsulation of healing agents. Polym. Chem. 2015, 6, 7100–7111. [Google Scholar] [CrossRef]
- Yan, J.; Ariyasivam, S.; Weerasinghe, D.; He, J.; Chisholm, B.; Chen, Z.; Webster, D. Thiourethane thermoset coatings from bio-based thiols. Polym. Int. 2011, 61, 602–608. [Google Scholar] [CrossRef]
- Jia, Y.; Shi, B.; Jin, J.; Li, J. High refractive index polythiourethane networks with high mechanical property via thiol-isocyanate click reaction. Polymer 2019, 180, 121746. [Google Scholar] [CrossRef]
- Podgórski, M.; Nair, D.P.; Chatani, S.; Berg, G.; Bowman, C.N. Programmable Mechanically Assisted Geometric Deformations of Glassy Two-Stage Reactive Polymeric Materials. ACS Appl. Mater. Interfaces 2014, 6, 6111–6119. [Google Scholar] [CrossRef] [PubMed]
- Podgórski, M.; Wang, C.; Bowman, C.N. Multiple shape memory polymers based on laminates formed from thiol-click chemistry based polymerizations. Soft Matter 2015, 11, 6852–6858. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, L.-T.T.; Truong, T.T.; Nguyen, H.T.; Le, L.; Nguyen, V.Q.; Van Le, T.; Luu, A.T. Healable shape memory (thio)urethane thermosets. Polym. Chem. 2015, 6, 3143–3154. [Google Scholar] [CrossRef]
- Gamardella, F.; Sabatini, V.; Ramis, X.; Serra, A. Tailor-made thermosets obtained by sequential dual-curing combining isocyanate-thiol and epoxy-thiol click reactions. Polymer 2019, 174, 200–209. [Google Scholar] [CrossRef]
- Gamardella, F.; Guerrero, F.; De la Flor, S.; Ramis, X.; Serra, A. A new class of vitrimers based on aliphatic poly(thiourethane) networks with shape memory and permanent shape reconfiguration. Eur. Polym. J. 2020, 122, 109361. [Google Scholar] [CrossRef]
- Gamardella, F.; Ramis, X.; De la Flor, S.; Serra, A. Preparation of poly(thiourethane) thermosets by controlled thiol-isocyanate click reaction using a latent organocatalyst. React. Funct. Polym. 2019, 134, 174–182. [Google Scholar] [CrossRef]
- Gamardella, F.; Muñoz, S.; De La Flor, S.; Ramis, X.; Serra, A. Recyclable Organocatalyzed Poly(Thiourethane) Covalent Adaptable Networks. Polymers 2020, 12, 2913. [Google Scholar] [CrossRef]
- Konuray, O.; Areny, N.; Morancho, J.M.; Fernàndez-Francos, X.; Serra, À.; Ramis, X. Preparation and characterization of dual-curable off-stoichiometric amine-epoxy thermosets with latent reactivity. Polymer 2018, 146, 42–52. [Google Scholar] [CrossRef]
- Konuray, O.; Liendo, F.; Fernández-Francos, X.; Serra, A.; Sangermano, M.; Ramis, X. Sequential curing of thiol-acetoacetate-acrylate thermosets by latent Michael addition reactions. Polymer 2017, 113, 193–199. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Gao, J.P.; Wang, Z.Y. Bicyclic Guanidinium Tetraphenylborate: A Photobase Generator and A Photocatalyst for Living Anionic Ring-Opening Polymerization and Cross-Linking of Polymeric Materials Containing Ester and Hydroxy Groups. J. Am. Chem. Soc. 2008, 130, 8130–8131. [Google Scholar] [CrossRef]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials; PWS Engineering Publishers: Boston, MA, USA, 1985. [Google Scholar]
- Shonaike, G.O.; Advani, S.G. Advanced Polymeric Materials: Structure Property Relationships; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Winter, H.H.; Chambon, F. Analysis of Linear Viscoelasticity of a Crosslinking Polymer at the Gel Point. J. Rheol. 1986, 30, 367–382. [Google Scholar] [CrossRef]
- Rogulska, M.; Kultys, A.; Olszewska, E. New thermoplastics poly(thiourethane-urethane) elastomers based on hexane-1,6-diyl diisocyanate (HDI). J. Therm. Anal. Calorim. 2013, 114, 903–916. [Google Scholar] [CrossRef] [Green Version]













| Sample | Mole Ratio (HDI/IPDI) (%) | Weight Ratio (S3/HDI/IPDI) (%) |
|---|---|---|
| HDI | 100:0 | 61:39:0 |
| 80HDI-20IPDI | 80:20 | 60:30:10 |
| 60HDI-40IPDI | 60:40 | 58:22:20 |
| 40HDI-60IPDI | 40:60 | 57:14:29 |
| 20HDI-80IPDI | 20:80 | 56:7:37 |
| IPDI | 0:100 | 54:0:46 |
| Rheometer | TGA | DMA | ||||||
|---|---|---|---|---|---|---|---|---|
| Sample | Gel Time 1 (min) | T2% 2 (°C) | TgE’ 3 (°C) | Tg-tanδ 4 (°C) | E’g 5 (GPa) | E’r 6 (MPa) | FWHM 7 (°C) | E’g/E’r |
| HDI | 48 | 276 | 44 | 57 | 2.3 | 10 | 8.5 | 164 |
| 80HDI-20IPDI | 58 | 273 | 55 | 65 | 2.3 | 12 | 10 | 176 |
| 60HDI-40IPDI | 83 | 269 | 75 | 85 | 2.8 | 12 | 11 | 200 |
| 40HDI-60IPDI | 120 | 269 | 84 | 97 | 2.9 | 13 | 13 | 223 |
| 20HDI-80IPDI | 133 | 269 | 97 | 108 | 3.0 | 14 | 13 | 214 |
| IPDI | 137 | 267 | 114 | 125 | 3.2 | 13 | 11 | 246 |
| Unconstrained | Fully-Constrained | Partially- Constrained | |||||
|---|---|---|---|---|---|---|---|
| Sample | Rr (%) | Vr (%/min) | TI-peak (°C) | TII-peak (°C) | Fmax (N) | Tpeak (°C) | Wrel mN/(mm/mm) |
| HDI | 98.0 | 13.5 | 44.8 | 57.0 | 7.4 | 42.8 | 501.5 |
| 80HDI-20IPDI | 98.0 | 12.4 | 60.3 | 70.8 | 8.5 | 58.6 | 542.7 |
| 60HDI-40IPDI | 97.5 | 11.1 | 74.0 | 88.2 | 9.3 | 72.4 | 560.5 |
| 40HDI-60IPDI | 97.6 | 12.3 | 86.3 | 99.9 | 9.1 | 84.8 | 585.9 |
| 20HDI-80IPDI | 96.8 | 11.9 | 105.0 | 111.2 | 7.6 | 102.0 | 503.1 |
| IPDI | 95.9 | 11.8 | 112.6 | 122.0 | 8.5 | 111.8 | 660.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamardella, F.; Serra, A.; Ramis, X.; De la Flor, S. Actuator Behaviour of Tailored Poly(thiourethane) Shape Memory Thermosets. Polymers 2021, 13, 1571. https://doi.org/10.3390/polym13101571
Gamardella F, Serra A, Ramis X, De la Flor S. Actuator Behaviour of Tailored Poly(thiourethane) Shape Memory Thermosets. Polymers. 2021; 13(10):1571. https://doi.org/10.3390/polym13101571
Chicago/Turabian StyleGamardella, Francesco, Angels Serra, Xavier Ramis, and Silvia De la Flor. 2021. "Actuator Behaviour of Tailored Poly(thiourethane) Shape Memory Thermosets" Polymers 13, no. 10: 1571. https://doi.org/10.3390/polym13101571
APA StyleGamardella, F., Serra, A., Ramis, X., & De la Flor, S. (2021). Actuator Behaviour of Tailored Poly(thiourethane) Shape Memory Thermosets. Polymers, 13(10), 1571. https://doi.org/10.3390/polym13101571