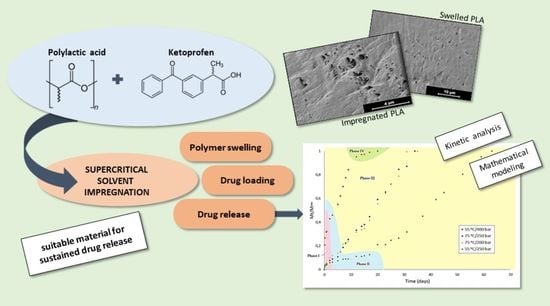
Supercritical Impregnation of Ketoprofen into Polylactic Acid for Biomedical Application: Analysis and Modeling of the Release Kinetic
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials and Reactants
2.2. Polymer Supercritical Impregnation and Swelling Analyses
2.3. SEM Studies
2.4. In Vitro Release Studies
3. Results
3.1. Supercritical Impregnation
3.1.1. Swelling Effect on PLA Filaments
3.1.2. Impregnation Loading of Ketoprofen into PLA Filaments
3.1.3. Optimization of the SSI of Ketoprofen into PLA Filaments
3.1.4. SEM Images
3.2. Drug Release Studies
4. Discussion
4.1. Supercritical Impregnation Analysis
4.1.1. Swelling Effect on PLA
4.1.2. Impregnation Loading of Ketoprofen into PLA Filaments
4.1.3. SEM Analysis
4.2. Ketoprofen Release Profiles
4.2.1. Analysis of the Ketoprofen Release Kinetics
4.2.2. Monophasic Models
4.2.3. Multiphasic Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Davis, S.S. Drug delivery systems. Interdiscip. Sci. Rev. 2000, 25, 175–183. [Google Scholar] [CrossRef]
- Braga, M.E.M.; Pato, M.T.V.; Silva, H.S.R.C.; Ferreira, E.I.; Gil, M.H.; Duarte, C.M.M.; de Sousa, H.C. Supercritical solvent impregnation of ophthalmic drugs on chitosan derivatives. J. Supercrit. Fluids 2008, 44, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Kazarian, S.G. Polymer Processing with Supercritical Fluids. Polym. Sci. 2000, 42, 78–101. [Google Scholar]
- Yu, J.P.; Guan, Y.X.; Yao, S.J.; Zhu, Z.Q. Preparation of roxithromycin-loaded poly(l-lactic acid) films with supercritical solution impregnation. Ind. Eng. Chem. Res. 2011, 50, 13813–13818. [Google Scholar] [CrossRef]
- Milovanovic, S.; Kuska, R.M.; Škorić-Lučić, M.L.; Kalagasidis-Krušić, M.T.; Frerich, S.; Žižović, I.T.; Ivanović, J.Z. Swelling kinetics and impregnation of PLA with thymol under supercritical CO2 conditions. Tehnika 2016, 71, 16–20. [Google Scholar] [CrossRef] [Green Version]
- Coutinho, I.T.; Champeau, M. Synergistic effects in the simultaneous supercritical CO2 impregnation of two compounds into poly(L-lactic acid) and polyethylene. J. Supercrit. Fluids 2020, 166, 105019. [Google Scholar] [CrossRef]
- Zhan, S.; Chen, C.; Zhao, Q.; Wang, W.; Liu, Z. Preparation of 5-Fu-loaded PLLA microparticles by supercritical fluid technology. Ind. Eng. Chem. Res. 2013, 52, 2852–2857. [Google Scholar] [CrossRef]
- Cabezas, L.I.; Fernández, V.; Mazarro, R.; Gracia, I.; de Lucas, A.; Rodríguez, J.F. Production of biodegradable porous scaffolds impregnated with indomethacin in supercritical CO2. J. Supercrit. Fluids 2012, 63, 155–160. [Google Scholar] [CrossRef]
- Cabezas, L.I.; Gracia, I.; De Lucas, A.; Rodríguez, J.F. Novel model for the description of the controlled release of 5-fluorouracil from PLGA and PLA foamed scaffolds impregnated in supercritical CO2. Ind. Eng. Chem. Res. 2014, 53, 15374–15382. [Google Scholar] [CrossRef]
- Milovanovic, S.; Markovic, D.; Markovic, A.; Kuska, R.M.; Zizovic, I.; Frerich, S.; Ivanovic, J. Supercritical CO2-assisted production of PLA and PLGA foams for controlled thymol release. Mater. Sci. Eng. C 2019, 99, 394–404. [Google Scholar] [CrossRef]
- Milovanovic, S.; Markovic, D.; Ivanovic, J. Added-value porous materials for controlled thymol release obtained by supercritical CO2 impregnation process. Cell Polym. 2019, 38, 153–166. [Google Scholar] [CrossRef]
- Weinstein, R.D.; Muske, K.R.; Martin, S.A.; Schaeber, D.D. Liquid and supercritical carbon dioxide-assisted implantation of ketoprofen into biodegradable sutures. Ind. Eng. Chem. Res 2010, 49, 7281–7286. [Google Scholar] [CrossRef]
- Champeau, M.; Coutinho, I.T.; Thomassin, J.M.; Tassaing, T.; Jérôme, C. Tuning the release profile of ketoprofen from poly (L-lactic acid) suture using supercritical CO2 impregnation process. J. Drug Deliv. Sci. Technol. 2020, 55, 101468. [Google Scholar] [CrossRef]
- Champeau, M.; Thomassin, J.-M.; Tassaing, T.; Jerome, C. Drug Loading of Sutures by Supercritical CO2 Impregnation: Effect of Polymer/Drug Interactions and Thermal Transitions. Macromol. Mater. Eng. 2015, 300, 596–610. [Google Scholar] [CrossRef]
- Manna, S.; Donnell, A.M.; Kaval, N.; Al-Rjoub, M.F.; Augsburger, J.J.; Banerjee, R.K. Improved design and characterization of PLGA/PLA-coated Chitosan based micro-implants for controlled release of hydrophilic drugs. Int. J. Pharm. 2018, 547, 122–132. [Google Scholar] [CrossRef]
- Marizza, P.; Pontoni, L.; Rindzevicius, T.; Alopaeus, J.F.; Su, K.; Zeitler, J.A.; Keller, S.S.; Kikic, I.; Moneghini, M.; De Zordi, N.; et al. Supercritical impregnation of polymer matrices spatially confined in microcontainers for oral drug delivery: Effect of temperature, pressure and time. J. Supercrit. Fluids 2016, 107, 145–152. [Google Scholar] [CrossRef]
- Veres, P.; López-Periago, A.M.; Lázár, I.; Saurina, J.; Domingo, C. Hybrid aerogel preparations as drug delivery matrices for low water-solubility drugs. Int. J. Pharm. 2015, 496, 360–370. [Google Scholar] [CrossRef] [Green Version]
- Goimil, L.; Braga, M.E.M.; Dias, A.M.A.; Gómez-Amoza, J.L.; Concheiro, A.; Alvarez-Lorenzo, C.; de Sousa, H.C.; García-González, C.A. Supercritical processing of starch aerogels and aerogel-loaded poly(ε-caprolactone) scaffolds for sustained release of ketoprofen for bone regeneration. J. CO2 Util. 2017, 18, 237–249. [Google Scholar] [CrossRef]
- Barros, A.A.; Oliveira, C.; Reis, R.L.; Lima, E.; Duarte, A.R.C. Ketoprofen-eluting biodegradable ureteral stents by CO2 impregnation: In vitro study. Int. J. Pharm. 2015, 495, 651–659. [Google Scholar] [CrossRef]
- Bastante, C.C.; Cardoso, L.C.; Serrano, C.M.; Martínez de La Ossa-Fernández, E.J. Supercritical impregnation of food packaging films to provide antioxidant properties. J. Supercrit. Fluids 2017, 128, 200–207. [Google Scholar] [CrossRef]
- Bastante, C.C.; Cardoso, L.C.; Fernández-Ponce, M.T.; Serrano, C.M.; Martínez de la Ossa-Fernández, E.J. Characterization of olive leaf extract polyphenols loaded by supercritical solvent impregnation into PET/PP food packaging films. J. Supercrit. Fluids 2018, 140, 196–206. [Google Scholar] [CrossRef]
- Gupta, R.B.; Shim, J.-J. Solubility in Supercritical Carbon Dioxide; CRC Press Taylor & Fracias Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Sabegh, M.A.; Rajaei, H.; Esmaeilzadeh, F.; Lashkarbolooki, M. Solubility of ketoprofen in supercritical carbon dioxide. J. Supercrit. Fluids 2012, 72, 191–197. [Google Scholar] [CrossRef]
- Méndez-Santiago, J.; Teja, A.S. The solubility of solids in supercritical fluids. Fluid Ph. Equilibria. 1999, 158–160, 501–510. [Google Scholar] [CrossRef]
- Üzer, S.; Akman, U.; Hortaçsu, Ö. Polymer swelling and impregnation using supercritical CO2: A model-component study towards producing controlled-release drugs. J. Supercrit. Fluids 2006, 38, 119–128. [Google Scholar] [CrossRef]
- Recommendations on methods for dosage forms testing. In European Pharmacopoeia 8.0; Council of Europe: Strasbourg, France, 2010; pp. 727–729.
- Mukae, K.; Bae, Y.H.; Kim, S.W.; Okano, T. A thermo-sensitive hydrogel: Poly(ethylene oxide-dimethyl siloxane-ethylene oxide)/poly(n-isopropyl acrylamide) interpenetrating polymer networks on-off regulation of solute release from thermo-sensitive hydrogel. Polym. J. 1990, 22, 250–265. [Google Scholar] [CrossRef]
- Champeau, M.; Thomassin, J.M.; Tassaing, T.; Jérôme, C. Drug loading of polymer implants by supercritical CO2 assisted impregnation: A review. J. Control. Release 2015, 209, 248–259. [Google Scholar] [CrossRef]
- Masmoudi, Y.; Ben Azzouk, L.; Forzano, O.; Andre, J.M.; Badens, E. Supercritical impregnation of intraocular lenses. J. Supercrit. Fluids 2011, 60, 98–105. [Google Scholar] [CrossRef]
- Bouledjouidja, A.; Masmoudi, Y.; Van Speybroeck, M.; Schueller, L.; Badens, E. Impregnation of Fenofibrate on mesoporous silica using supercritical carbon dioxide. Int. J. Pharm. 2016, 499, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bouledjouidja, A.; Masmoudi, Y.; Sergent, M.; Badens, E. Effect of operational conditions on the supercritical carbon dioxide impregnation of anti-inflammatory and antibiotic drugs in rigid commercial intraocular lenses. J. Supercrit. Fluids 2017, 130, 63–75. [Google Scholar] [CrossRef]
- Zhao, J.; Farhatnia, Y.; Kalaskar, D.M.; Zhang, Y.; Bulter, P.E.M.; Seifalian, A.M. The influence of porosity on the hemocompatibility of polyhedral oligomeric silsesquioxane poly (caprolactone-urea) urethane. Int. J. Biochem. Cell Biol. 2015, 68, 176–186. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Ghanbari, H.; Cousins, B.G.; Hamilton, G.; Seifalian, A.M. Small calibre polyhedral oligomeric silsesquioxane nanocomposite cardiovascular grafts: Influence of porosity on the structure, haemocompatibility and mechanical properties. Acta Biomater. 2011, 7, 3857–3867. [Google Scholar] [CrossRef]
- Pini, R.; Storti, G.; Mazzotti, M.; Tai, H.; Shakesheff, K.M.; Howdle, S.M. Sorption and swelling of poly(DL-lactic acid) and poly(lactic-co-glycolic acid) in supercritical CO2: An experimental and modeling study. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 483–496. [Google Scholar] [CrossRef]
- Champeau, M.; Thomassin, J.M.; Jérôme, C.; Tassaing, T. In situ FTIR micro-spectroscopy to investigate polymeric fibers under supercritical carbon dioxide: CO2 sorption and swelling measurements. J. Supercrit. Fluids 2014, 90, 44–52. [Google Scholar] [CrossRef]
- Ivanovic, J.; Knauer, S.; Fanovich, A.; Milovanovic, S.; Stamenic, M.; Jaeger, P.; Zizovica, I.; Eggers, R. Supercritical CO2 sorption kinetics and thymol impregnation of PCL and PCL-HA. J. Supercrit. Fluids 2016, 107, 486–498. [Google Scholar] [CrossRef]
- Aionicesei, E.; Škerget, M.; Knez, Ž. Measurement of CO2 solubility and diffusivity in poly(l-lactide) and poly(d,l-lactide-co-glycolide) by magnetic suspension balance. J. Supercrit. Fluids 2008, 47, 296–301. [Google Scholar] [CrossRef]
- Goodship, V.; Ogur, E.O. Polymer Processing with Supercritical Fluids; Rapra Technology Ltd.: Shawbury, UK, 2004; Volume 15. [Google Scholar]
- Kuska, R.M.; Milovanovic, S.; Frerich, S.; Ivanovic, J. Thermal analysis of polylactic acid under high CO2 pressure applied in supercritical impregnation and foaming process design. J. Supercrit. Fluids 2019, 144, 71–80. [Google Scholar] [CrossRef]
- Fu, Y.; Kao, W.J. Drug release kinetics and transport mechanisms of non-degradable and degradable polymeric delivery systems. Expert Opin. Drug Deliv. 2010, 7, 429–444. [Google Scholar] [CrossRef]
- Fredenberg, S.; Wahlgren, M.; Reslow, M.; Axelsson, A. The mechanisms of drug release in poly(lactic-co-glycolic acid)-based drug delivery systems—A review. Int. J. Pharm. 2011, 415, 34–52. [Google Scholar] [CrossRef]
- Wang, J.; Wang, B.M.; Schwendeman, S.P. Characterization of the initial burst release of a model peptide from poly(d,l-lactide-co-glycolide) microspheres. J. Control. Release 2002, 82, 289–307. [Google Scholar] [CrossRef]
- Wang, X.; Venkatraman, S.S.; Boey, F.Y.C.; Loo, J.S.C.; Tan, L.P. Controlled release of sirolimus from a multilayered PLGA stent matrix. Biomaterials 2006, 27, 5588–5595. [Google Scholar] [CrossRef]
- Duvvuri, S.; Janoria, K.G.; Mitra, A.K. Effect of polymer blending on the release of ganciclovir from PLGA microspheres. Pharm. Res. 2006, 23, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.E.; Son, J.S.; Park, K.; Han, D.K. Fabrication of covered porous PLGA microspheres using hydrogen peroxide for controlled drug delivery and regenerative medicine. J. Control. Release 2009, 133, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Gao, S.-Z.; Zhang, X.-H.; Tian, H.-B.; Wang, H.-T.; Shang, Z.-H. Preparation of aclarubicin PLGA nanospheres and related in vitro/in vivo studies. J. Appl. Polym. Sci. 2010, 117, 2754–2761. [Google Scholar] [CrossRef]
- Gorrasi, G.; Pantani, R. Hydrolysis and Biodegradation of Poly (lactic acid). In Synthesis, Structure and Properties of Poly (Lactic Acid). Advances in Polymer Science; Di Lorenzo, M., Androsch, R., Eds.; Springer: Cham, Switzerland, 2017; Volume 279. [Google Scholar]
- Goto, T.; Kishita, M.; Sun, Y.; Sako, T.; Okajima, I. Degradation of Polylactic Acid Using Sub-Critical Water for Compost. Polymers 2020, 12, 2434. [Google Scholar] [CrossRef]
- Higuchi, T. Rate of release of medicaments from ointment bases containing drugs in suspension. J. Pharm. Sci. 1961, 50, 874–875. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–343. [Google Scholar] [CrossRef]
- Basu, T.; Pal, B.; Singh, S. Fabrication of core–shell PLGA/PLA–pNIPAM nanocomposites for improved entrapment and release kinetics of antihypertensive drugs. Particuology 2018, 40, 169–176. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Peppas, N.A. Effect of the morphology of hydrophilic polymeric matrices on the diffusion and release of water soluble drugs. J. Membr. Sci. 1981, 9, 211–227. [Google Scholar] [CrossRef]
- Ritger, P.L.; Peppas, N.A. A simple equation for description of solute release II. Fickian and anomalous release from swellable devices. J. Control. Release 1987, 5, 37–42. [Google Scholar] [CrossRef]
- Abasian, P.; Radmansouri, M.; Jouybari, M.H.; Ghasemi, M.V.; Mohammadi, A.; Irani, M.; Jazi, F.S. Incorporation of magnetic NaX zeolite/DOX into the PLA/chitosan nanofibers for sustained release of doxorubicin against carcinoma cells death in vitro. Int. J. Biol. Macromol. 2019, 121, 398–406. [Google Scholar] [CrossRef]
- Das, D.; Das, R.; Mandal, J.; Ghosh, A.; Pal, S. Dextrin crosslinked with poly(lactic acid): A novel hydrogel for controlled drug release application. J. Appl. Polym. Sci. 2014, 131, 40039. [Google Scholar] [CrossRef]
- Peppas, N.A.; Sahlin, J.J. A simple equation for the description of solute release. III. Coupling of diffusion and relaxation. Int. J. Pharm. 1989, 57, 169–172. [Google Scholar] [CrossRef]
- Bruschi, M.L. (Ed.) Mathematical models of drug release. In Strategies to Modify the Drug Release from Pharmaceutical Systems; Woodhead Publishing: Sawston, UK, 2015; pp. 63–86. [Google Scholar] [CrossRef]
- Abulateefeh, S.R.; Alkawareek, M.Y.; Alkilany, A.M. Tunable sustained release drug delivery system based on mononuclear aqueous core-polymer shell microcapsules. Int. J. Pharm. 2019, 558, 291–298. [Google Scholar] [CrossRef]
- Moorkoth, D.; Nampoothiri, K.M.; Nagarajan, S.; Girija, A.R.; Balasubramaniyan, S.; Kumar, D.S. Star-Shaped Polylactide Dipyridamole Conjugated to 5-Fluorouracil and 4-Piperidinopiperidine Nanocarriers for Bioimaging and Dual Drug Delivery in Cancer Cells. ACS Appl. Polym. Mater. 2021, 3, 737–756. [Google Scholar] [CrossRef]
- Öztürk, A.A.; Yenilmez, E.; Şenel, B.; Kıyan, H.T.; Güven, U.M. Effect of different molecular weight PLGA on flurbiprofen nanoparticles: Formulation, characterization, cytotoxicity, and in vivo anti-inflammatory effect by using HET-CAM assay. Drug Dev. Ind. Pharm. 2020, 46, 682–695. [Google Scholar] [CrossRef]









| Fixed Parameters | Varying Parameters | Response | |||
|---|---|---|---|---|---|
| Swelling study | CO2 flow until target pressure Contact time Depressurization rate Amount of PLA | 10 g/min 0.5 h 100 bar/min 0.3 g | Pressure Temperature | 100, 250, 400 bar 35, 55, 75 °C | Swelling |
| SSI | CO2 flow until target pressure Contact time Depressurization rate Amount of PLA Amount of KET | 10 g/min 2 h 100 bar/min 0.3 g Saturation | Pressure Temperature | 100, 250, 400 bar 35, 55, 75 °C | Swelling Drug loading |
| Df | Sum Sq | Mean Sq | F-Value | p-Value | |
|---|---|---|---|---|---|
| A: Pressure | 1 | 144.354 | 144.354 | 18.90 | 0.0225 |
| B: Temperature | 1 | 138.913 | 138.913 | 18.19 | 0.0236 |
| AA | 1 | 15.9989 | 15.9989 | 2.10 | 0.2436 |
| AB | 1 | 107.33 | 107.33 | 14.06 | 0.0331 |
| BB | 1 | 15.9989 | 15.9989 | 2.10 | 0.2436 |
| Error | 3 | 22.9088 | 7.63626 | - | - |
| Total | 8 | 445.503 | - | - | - |
| Df | Sum Sq | Mean Sq | F-Value | p-Value | |
|---|---|---|---|---|---|
| A: Pressure | 1 | 165.585 | 165.585 | 51.53 | 0.0056 |
| B: Temperature | 1 | 297.229 | 297.229 | 92.50 | 0.0024 |
| AA | 1 | 0.00269 | 0.00269 | 0.00 | 0.9787 |
| AB | 1 | 115.348 | 115.348 | 35.90 | 0.0093 |
| BB | 1 | 31.0209 | 31.0209 | 9.65 | 0.0530 |
| Error | 3 | 9.63964 | 3.21321 | - | - |
| Total | 8 | 618.825 | - | - | - |
| Df | Sum Sq | Mean Sq | F-Value | p-Value | |
|---|---|---|---|---|---|
| A: Pressure | 1 | 18.9038 | 18.9038 | 5.36 | 0.1034 |
| B: Temperature | 1 | 54.5414 | 54.5414 | 15.48 | 0.0292 |
| AA | 1 | 3.65401 | 3.65401 | 1.04 | 0.3835 |
| AB | 1 | 19.404 | 19.404 | 5.51 | 0.1006 |
| BB | 1 | 9.31681 | 9.31681 | 2.64 | 0.2024 |
| Error | 3 | 10.5708 | 3.52358 | - | - |
| Total | 8 | 116.391 | - | - | - |
| Df | Sum Sq | Mean Sq | F-Value | p-Value | |
|---|---|---|---|---|---|
| A: Pressure | 1 | 19.9838 | 19.9838 | 2.30 | 0.2266 |
| B: Temperature | 1 | 171.521 | 171.521 | 19.74 | 0.0212 |
| AA | 1 | 0.166272 | 0.166272 | 0.02 | 0.8987 |
| AB | 1 | 3.59102 | 3.59102 | 0.41 | 0.5660 |
| BB | 1 | 6.82036 | 6.82036 | 0.79 | 0.4409 |
| Error | 3 | 26.0642 | 8.68805 | - | - |
| Total | 8 | 228.147 | - | - | - |
| Impregnating Conditions | |||||
|---|---|---|---|---|---|
| 55 °C, 400 bar | 75 °C, 250 bar | 75 °C, 200 bar | 55 °C, 250 bar | ||
| Zero-order | 0.8780 | 0.9936 | 0.9824 | 0.9452 | |
| 0.0459 | 0.0287 | 0.0282 | 0.0149 | ||
| First-order | 0.8162 | 0.8484 | 0.8668 | 0.9536 | |
| 0.0735 | 0.1022 | 0.0919 | 0.0551 | ||
| Higuchi | 0.9747 | 0.9002 | 0.8781 | 0.7775 | |
| 0.2207 | 0.1640 | 0.1610 | 0.1089 | ||
| Korsmeyer–Peppas | 0.9625 | 0.9757 | 0.9737 | 0.8012 | |
| 0.3786 | 0.0591 | 0.0737 | 0.0449 | ||
| 0.3224 | 0.6219 | 0.5367 | 0.5571 | ||
| Peppas–Sahlin | 0.5533 | 0.8818 | 0.7674 | 0.4846 | |
| 0.4571 | 0.0123 | 0.0317 | 0.0158 | ||
| −0.0587 | 0.0337 | 0.0282 | 0.0147 | ||
| Impregnating Conditions | |||||
|---|---|---|---|---|---|
| 55 °C, 400 bar | 75 °C, 250 bar | 75 °C, 200 bar | 55 °C, 250 bar | ||
| Phases I & II | 0.9970 | 0.9949 | 0.9933 | 0.9885 | |
| 0.3590 | 0.0526 | 0.0696 | 0.0503 | ||
| 0.2348 | 0.4491 | 0.4424 | 0.2501 | ||
| 5 | 5 | 5 | 12 | ||
| 0.55 | 0.11 | 0.14 | 0.09 | ||
| Phase III | 0.9991 | 0.9943 | 0.9904 | 0.9938 | |
| 0.1682 | 0.0231 | 0.0214 | 0.0016 | ||
| 0.7328 | 1.0659 | 1.0856 | 1.5587 | ||
| 14 | 34 | 35 | 63 | ||
| 0.97 | 1.00 | 1.00 | 1.00 | ||
| Phase IV | 0.9917 | ||||
| 0.7807 | |||||
| 0.0829 | _ | _ | _ | ||
| 20 | |||||
| 1.00 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verano Naranjo, L.; Cejudo Bastante, C.; Casas Cardoso, L.; Mantell Serrano, C.; Martínez de la Ossa Fernández, E.J. Supercritical Impregnation of Ketoprofen into Polylactic Acid for Biomedical Application: Analysis and Modeling of the Release Kinetic. Polymers 2021, 13, 1982. https://doi.org/10.3390/polym13121982
Verano Naranjo L, Cejudo Bastante C, Casas Cardoso L, Mantell Serrano C, Martínez de la Ossa Fernández EJ. Supercritical Impregnation of Ketoprofen into Polylactic Acid for Biomedical Application: Analysis and Modeling of the Release Kinetic. Polymers. 2021; 13(12):1982. https://doi.org/10.3390/polym13121982
Chicago/Turabian StyleVerano Naranjo, Lidia, Cristina Cejudo Bastante, Lourdes Casas Cardoso, Casimiro Mantell Serrano, and Enrique José Martínez de la Ossa Fernández. 2021. "Supercritical Impregnation of Ketoprofen into Polylactic Acid for Biomedical Application: Analysis and Modeling of the Release Kinetic" Polymers 13, no. 12: 1982. https://doi.org/10.3390/polym13121982
APA StyleVerano Naranjo, L., Cejudo Bastante, C., Casas Cardoso, L., Mantell Serrano, C., & Martínez de la Ossa Fernández, E. J. (2021). Supercritical Impregnation of Ketoprofen into Polylactic Acid for Biomedical Application: Analysis and Modeling of the Release Kinetic. Polymers, 13(12), 1982. https://doi.org/10.3390/polym13121982