Self-Stable Precipitation Polymerization Molecular Entanglement Effect and Molecular Weight Simulations and Experiments
Abstract
:1. Introduction
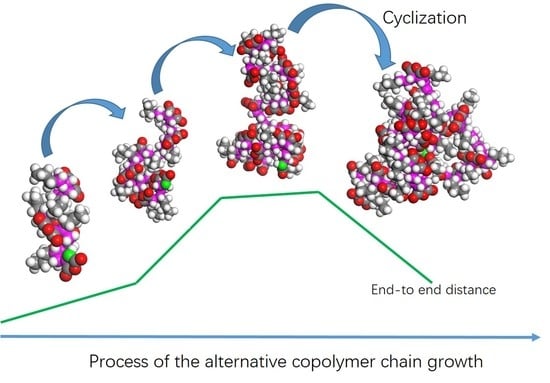
2. Simulation Method and Results
3. Comparison with Experimental Results
3.1. Experiment Procedure
3.2. Comparison of Molecular Weight
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yan, Q.; Bai, Y.; Meng, Z. Synthesis of Narrow Disperse Crosslinked Poly(divinylbenzene) Microspheres in Acetic acid via Precipitation Polymerization. Acta. Polym. Sin. 2007, 11, 1102–1104. (In Chinese) [Google Scholar] [CrossRef]
- Yan, Q.; Bai, Y.; Meng, Z.; Yang, W. Precipitation Polymerization in Acetic Acid, Synthesis of Monodisperse Cross-Linked Poly(divinylbenzene) Microspheres. J. Phys. Chem. B 2008, 112, 6914–6922. [Google Scholar] [CrossRef]
- Yan, Q.; Zhao, T.; Bai, Y.; Zhang, F.; Yang, W. Precipitation Polymerization in Acetic Acid, Study of the Solvent Effect on the Morphology of Poly(divinylbenzene). J. Phys. Chem. B 2009, 113, 3008–3014. [Google Scholar] [CrossRef] [PubMed]
- Xing, C.M.; Yang, W.T. Stabilizer-free Dispersion Copolymerization of Maleic Anhydride and Vinyl Acetate. I. Effects of Principal Factors on Microspheres. J. Polym. Sci. Part A Polym. Chem. 2005, 43, 3760–3770. [Google Scholar] [CrossRef]
- Xing, C.M.; Yang, W.T. A novel, facile method for the preparation of uniform, reactive maleic anhydride vinyl acetate copolymer micro- and nanospheres. Macromol. Rapid Commun. 2004, 25, 1568–1574. [Google Scholar] [CrossRef]
- Hao, G.L.; Liu, Z.J.; Deng, J.Y.; Yang, W.T. Nucleation and Particle Growth Mechanism of Monodisperse Microspheres of PSMA in Self-Stable Precipitation Polymerization. J. Beijing Univ. Chem. Technol. (Nat. Sci. Ed.) 2010, 37, 98–102. (In Chinese) [Google Scholar]
- Liu, Z.; Chen, D.; Zhang, J.; Liao, H.; Chen, Y.; Sun, Y.; Deng, J.; Yang, W. Self-Stabilized Precipitation Polymerization and Its Application. Research 2018, 1, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, G.; Zhou, L.; Zhang, P.; Zhao, E.; Zhou, L.; Chen, D.; Sun, J.; Gu, X.; Yang, W.; Tang, B.Z. Fluorescence Self-Reporting Precipitation Polymerization Based on Aggregation-Induced Emission for Constructing Optical Nanoagents. Angew. Chem. 2020, 59, 10122–10128. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Xing, R.; Yan, X. Peptide Self-assembly Thermodynamics and Kinetics. Chem. Soc. Rev. 2016, 45, 5589–5604. [Google Scholar] [CrossRef]
- Srinivas, G.; Shelley, J.C.; Nielsen, S.O.; Discher, D.E.; Klein, M.L. Simulation of Diblock Copolymer Self-Assembly Using a Coarse-Grain Model. J. Phys. Chem. B 2004, 108, 8153–8160. [Google Scholar] [CrossRef] [Green Version]
- Karim, F.; Hossein, A.; Florian, M.; Michael, C. Reactive Molecular Dynamics with Material-Specific Coarse-Grained Potentials Growth of Polystyrene Chains from Styrene Monomers. J. Phys. Chem. B 2010, 114, 13656–13666. [Google Scholar]
- Liu, H.; Zhu, Y.L.; Lu, Z.Y. A kinetic Chain Growth Algorithm in Coarse-grained Simulations. J. Comput. Chem. 2016, 30, 2634–2646. [Google Scholar] [CrossRef]
- Jang, C.; Lacy, T.E.; Gwaltney, S.R.; Toghiani, H.; Pittman, C.U. Relative Reactivity Volume Criterion for Cross-Linking, Application to Vinyl Ester Resin Molecular Dynamics Simulations. Macromolecules 2012, 45, 4876–4885. [Google Scholar] [CrossRef]
- Torres-Knoop, A.; Kryven, I.; Schamboeck, V.; Iedema, P. Modeling the Free-radical Polymerization of Hexanediol Diacrylate (HDDA) a Molecular Dynamics and Graph Theory Approach. Soft Matter 2018, 14, 3404–3414. [Google Scholar] [CrossRef] [Green Version]
- Jiwon, J.; Chanwook, P.; Gun, J.Y. Free Radical Polymerization Simulation and Molecular Entanglement Effect on Large Deformation Behavior. Eur. Polym. J. 2019, 114, 223–233. [Google Scholar]
- Kokubo, T.; Iwatsuki, S.; Yamashita, Y. Studies on Charge-Transfer Complex and Polymerization. XX. Terpolymerizations with the Anethole-Maleic Anhydride Alternating Copolymerization Stystem. Macromolecules 1998, 3, 518–523. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase Applications Overview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Berezkin, A.V.; Khalatur, P.G.; Khokhlov, A.R. Computer Modeling of Synthesis of Proteinlike Copolymer via Copolymerization with Simultaneous Globule Formation. J. Chem. Phys. 2003, 118, 8049–8060. [Google Scholar] [CrossRef]
- Berezkin, A.V.; Khalatur, P.G.; Khokhlov, A.R.; Reineker, P. Molecular Dynamics Simulation of the Synthesis of Protein-like Copolymers via Conformation-dependent Design. New J. Phys. 2004, 6, 44. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.F. Preparation of Functional Microspheres of Maleic Anhydride and C5 Fraction by Meta-stable Precipition Polymerization. Master’s Thesis, Beijing University of Chemical Technology, Beijing, China, 15 June 2012. [Google Scholar]
- Sclavons, M.; Franquinet, P.; Carlier, V. Quantification of the Maleic Anhydride Grafted onto Polypropylene by Chemical and Viscosimetric Titrations, and FTIR Spectroscopy. Polymer 2000, 41, 1989–1999. [Google Scholar] [CrossRef]
- Alfred, R.; Howard, L.; Hoegy, W. Universal Calibration in GPC. J. Polym. Sci. Part A-1 Polym. Chem. 1972, 10, 217–235. [Google Scholar]
- Victoria, D.; Herrera-Ordonez, J.; Cristy, L.A.R.; Estevez, M. Autoacceleration in Bulk Free-Radical Polymerization Effect of Chain Transfer. Macromol. Chem. Phys. 2018, 219, 1700434. [Google Scholar] [CrossRef]








| Chain | DP | End-to-End Distance (Å) | Rg (Å) |
|---|---|---|---|
| 1PM1 | 5 | 12 | 5.0 |
| 1PM1 | 10 | 15 | 7.5 |
| 1PM1 | 15 | 18 | 10.1 |
| 1PM1 | 20 | 27 | 11.5 |
| 1PM1 | 25 | 30 | 11.6 |
| 1PM1 | 30(end) | 17 | 10.2 |
| CPM1 | 5 | 10 | 5.0 |
| CPM1 | 10 | 15 | 7.5 |
| CPM1 | 15 | 30 | 10.5 |
| CPM1 | 20(end) | 11 | 9.4 |
| Polymer | DP | Ni |
|---|---|---|
| 1PM | 26 | 1 |
| 1PM | 27 | 2 |
| 1PM | 30 | 8 |
| 1PM | 32 | 7 |
| 1PM | 34 | 2 |
| 1PM | 61 | 2 |
| 1PM | 80 | 1 |
| CPM | 17 | 1 |
| CPM | 20 | 5 |
| CPM | 23 | 7 |
| CPM | 28 | 5 |
| CPM | 30 | 4 |
| CPM | 37 | 3 |
| CPM | 60 | 1 |
| Polymer | Mn (g/mol) | Mw (g/mol) | PDI |
|---|---|---|---|
| 1PMsimulation | 6001 | 7531 | 1.25 |
| 1PMexperiment | 5550 | 7660 | 1.38 |
| CPMsimulation | 4581 | 5028 | 1.10 |
| CPMexperiment | 4517 | 5150 | 1.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, J.; Gao, Y.; Yang, W. Self-Stable Precipitation Polymerization Molecular Entanglement Effect and Molecular Weight Simulations and Experiments. Polymers 2021, 13, 2243. https://doi.org/10.3390/polym13142243
Qu J, Gao Y, Yang W. Self-Stable Precipitation Polymerization Molecular Entanglement Effect and Molecular Weight Simulations and Experiments. Polymers. 2021; 13(14):2243. https://doi.org/10.3390/polym13142243
Chicago/Turabian StyleQu, Jiali, Yi Gao, and Wantai Yang. 2021. "Self-Stable Precipitation Polymerization Molecular Entanglement Effect and Molecular Weight Simulations and Experiments" Polymers 13, no. 14: 2243. https://doi.org/10.3390/polym13142243
APA StyleQu, J., Gao, Y., & Yang, W. (2021). Self-Stable Precipitation Polymerization Molecular Entanglement Effect and Molecular Weight Simulations and Experiments. Polymers, 13(14), 2243. https://doi.org/10.3390/polym13142243