Electrically Tuneable Optical Diffraction Gratings Based on a Polymer Scaffold Filled with a Nematic Liquid Crystal
Abstract
:1. Introduction
2. Experimental Investigation
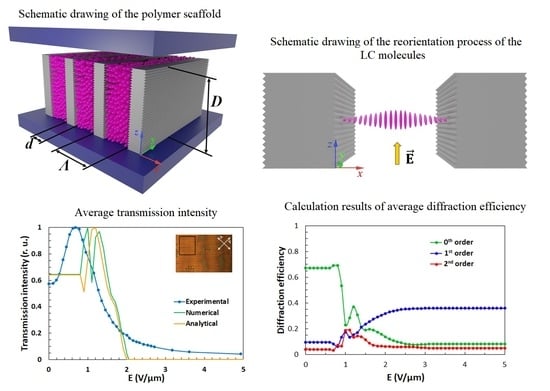
2.1. Fabrication and Operation of Grating Structures
2.2. Optical Properties
3. Orientational Profile of the Liquid Crystalline Medium
3.1. Minimization of Free Energy
3.2. Comparison of Analytical and Numerical Results
4. Theoretical Analysis of Optical Properties
4.1. Calculation of Optical Transmission Properties
4.2. Calculation of Optical Diffraction Properties
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- O’Shea, D.C.; Suleski, T.J.; Kathman, A.D.; Prather, D.W. Diffractive Optics: Design, Fabrication, and Test; SPIE Press: Bellingham, WA, USA, 2003. [Google Scholar]
- Soskind, Y.G. Field Guide to Diffractive Optics. In Field Guide to Diffractive Optics; SPIE Press: Bellingham, WA, USA, 2011. [Google Scholar]
- Huang, K.; Shi, P.; Kang, X.-L.; Zhang, X.; Li, Y.-P. Design of DOE for generating a needle of a strong longitudinally polarized field. Opt. Lett. 2010, 35, 965–967. [Google Scholar] [CrossRef]
- Cojoc, D.; Di Fabrizio, E.; Businaro, L.; Cabrini, S.; Romanato, F.; Vaccari, L.; Altissimo, M. Design and fabrication of diffractive optical elements for optical tweezer arrays by means of e-beam lithography. Microelectron. Eng. 2002, 61-62, 963–969. [Google Scholar] [CrossRef]
- Komanduri, R.K.; Oh, C.; Escuti, M.J. 34.4L: Late-News Paper: Polarization Independent Projection Systems Using Thin Film Polymer Polarization Gratings and Standard Liquid Crystal Microdisplays. SID Symp. Dig. Tech. Pap. 2009, 40, 487–490. [Google Scholar] [CrossRef]
- Seo, E.; Kee, H.C.; Kim, Y.; Jeong, S.; Choi, H.; Lee, S.; Kim, J.; Komanduri, R.K.; Escuti, M.J. 39.2: Polarization Conversion System Using a Polymer Polarization Grating. SID Symp. Dig. Tech. Pap. 2011, 42, 540–543. [Google Scholar] [CrossRef] [Green Version]
- Parikka, M.; Kaikuranta, T.; Laakkonen, P.; Lautanen, J.; Tervo, J.; Honkanen, M.; Kuittinen, M.; Turunen, J. Deterministic diffractive diffusers for displays. Appl. Opt. 2001, 40, 2239–2246. [Google Scholar] [CrossRef] [PubMed]
- De Sterke, C.M.; van der Laan, C.J.; Frankena, H.J. Non-polarizing beam splitter design. J. Appl. Opt. 1983, 22, 595–601. [Google Scholar] [CrossRef]
- Cao, B.X.; Hoang, P.L.; Ahn, S.; Kim, J.; Sohn, H.; Noh, J. Real-time detection of focal position of work piece surface during laser processing using diffractive beam samplers. Opt. Lasers Eng. 2016, 86, 92–97. [Google Scholar] [CrossRef]
- Katz, S.; Kaplan, N.; Grossinger, I. Using Diffractive Optical Elements: DOEs for beam shaping-fundamentals and applications. Laser Tech. J. 2018, 15, 29–32. [Google Scholar] [CrossRef] [Green Version]
- Kizuka, Y.; Yamauchi, M.; Matsuoka, Y. Characteristics of a laser beam spot focused by a binary diffractive axicon. Opt. Eng. 2008, 47, 053401. [Google Scholar] [CrossRef]
- Yuan, X.-C.; Lin, J.; Bu, J.; Burge, R.E. Achromatic design for the generation of optical vortices based on radial spiral phase plates. Opt. Express 2008, 16, 13599–13605. [Google Scholar] [CrossRef]
- Wang, Q.-H.; Ji, C.-C.; Li, L.; Deng, H. Dual-view integral imaging 3D display by using orthogonal polarizer array and po-larization switcher. Opt. Express 2016, 24, 9–16. [Google Scholar] [CrossRef]
- Mi, L.; Chen, C.P.; Lu, Y.; Zhang, W.; Chen, J.; Maitlo, N. Design of lensless retinal scanning display with diffractive optical element. Opt. Express 2018, 27, 20493–20507. [Google Scholar] [CrossRef]
- Kress, B.C. Optical Architectures for Augmented-, Virtual-, and Mixed-Reality Headsets; SPIE Press: Bellingham, WA, USA, 2020. [Google Scholar]
- Khan, M.S.; Saeed, W.M.; Roth, B.; Lachmayer, R. Diffractive optics based automotive lighting system. A rear end lamp design for communication between road users. Adv. Opt. Technol. 2020, 10, 49–57. [Google Scholar] [CrossRef]
- Dahlke, D.; Geßner, M.; Meißner, H.; Stebner, K.; Grießbach, D.; Berger, R.; Börner, A. Calibrating photogrammetric airborne camera system with diffractive optical elements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 1637–1642. [Google Scholar] [CrossRef] [Green Version]
- Kern, C.; Speck, U.; Riesenberg, R.; Reble, C.; Khazaka, G.; Zieger, M.; Kaatz, M.; De Gregorio, M.; Fischer, F. Mobile snapshot hyperspectral imaging device for skin evaluation using diffractive optical elements. Ski. Res. Technol. 2021, 00, 1–10. [Google Scholar] [CrossRef]
- Fei, B. Hyperspectral imaging in medical applications. Data Handling Sci. Technol. 2020, 32, 523–565. [Google Scholar] [CrossRef]
- Hettrick, M.C. Surface normal rotation: A new technique for grazing-incidence monochromators. Appl. Opt. 1992, 31, 7174–7178. [Google Scholar] [CrossRef] [PubMed]
- Kneubühl, F. Diffraction Grating Spectroscopy. Appl. Opt. 1969, 8, 505–519. [Google Scholar] [CrossRef]
- Laude, J.-P.; Lerner, J.M. Wavelength Division Multiplexing/Demultiplexing (WDM) Using Diffraction Gratings. In Proceedings of the 28th Annual Technical Symposium, San Diego, CA, USA, 12 December 1984; Volume 503, pp. 22–28. [Google Scholar]
- Harvey, K.C.; Myatt, C.J. External-cavity diode laser using a grazing-incidence diffraction grating. Opt. Lett. 1991, 16, 910–912. [Google Scholar] [CrossRef] [PubMed]
- Treacy, E. Optical pulse compression with diffraction gratings. IEEE J. Quantum Electron. 1969, 5, 454–458. [Google Scholar] [CrossRef]
- James, S.; Tatam, R. Optical fibre long-period grating sensors: Characteristics and application. Meas. Sci. Technol. 2003, 14, R49–R61. [Google Scholar] [CrossRef] [Green Version]
- Fattal, D.; Peng, Z.; Tran, T.; Vo, S.; Fiorentino, M.; Brug, J.; Beausoleil, R.G. A multi-directional backlight for a wide-angle, glasses-free three-dimensional display. Nat. Cell Biol. 2013, 495, 348–351. [Google Scholar] [CrossRef]
- Tien, C.-L.; Lin, R.-J.; Kang, C.-C.; Huang, B.-Y.; Kuo, C.-T.; Huang, S.-Y. Electrically Controlled Diffraction Grating in Azo Dye-Doped Liquid Crystals. Polymers 2019, 11, 1051. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.-Y.; Huang, B.-Y.; Kang, C.-C.; Kuo, C.-T. Diffraction and Polarization Properties of Electrically–Tunable Nematic Liquid Crystal Grating. Polymers 2020, 12, 1929. [Google Scholar] [CrossRef]
- Chen, C.Y.; Hsieh, C.F.; Lin, Y.F.; Pan, R.P.; Pan, C.L. Magnetically tunable room-temperature 2π liquid crystal terahertz phase shifter. Opt. Express 2004, 12, 2625–2630. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Liu, H.; Han, X.; Lu, W.; Tao, Z.Y. A magnetically tunable non-Bragg defect mode in a corrugated wave-guide filled with liquid crystals. Phys. Lett. A 2018, 382, 1000–1005. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, P.-X.; D’Acierno, F.; Hamad, W.Y.; Michal, C.A.; MacLachlan, M.J. Tunable Diffraction Gratings from Bio-sourced Lyotropic Liquid Crystals. Adv. Mater. 2020, 1907376, 1–9. [Google Scholar]
- Ono, H.; Takahashi, F.; Emoto, A.; Kawatsuki, N. Polarization holograms in azo dye-doped polymer dissolved liquid crystal composites. J. Appl. Phys. 2005, 97, 53508. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Zhao, Y. Tunable diffraction gratings based on azobenzene polymers and liquid crystals. In Smart Light Responsive Materi-als—Azobenzene-Containing Polymers and Liquid Crystals; Zhao, Y., Ikeda, T., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 363–410. [Google Scholar]
- Gregorc, M.; Li, H.; Domenici, V.; Drevenšek-Olenik, I. Tunable photonic structures from liquid crystal elastomers. Proc. SPIE 2012, 8556, 855616. [Google Scholar]
- Bošnjaković, D.; Gregorc, M.; Li, H.; Čopič, M.; Domenici, V.; Drevenšek-Olenik, I. Mechanical Manipulation of Diffractive Properties of Optical Holographic Gratings from Liquid Crystalline Elastomers. Appl. Sci. 2018, 8, 1330. [Google Scholar] [CrossRef] [Green Version]
- Nieborek, M.; Rutkowska, K.; Woliński, T.R.; Bartosewicz, B.; Jankiewicz, B.; Szmigiel, D.; Kozanecka-Szmigiel, A. Tunable Polarization Gratings Based on Nematic Liquid Crystal Mixtures Photoaligned with AzoPolymer-Coated Substrates. Crystals 2020, 10, 768. [Google Scholar] [CrossRef]
- Zola, R.S.; Bisoyi, H.K.; Wang, H.; Urbas, A.M.; Bunning, T.J.; Li, Q. Dynamic Control of Light Direction Enabled by Stimu-li-Responsive Liquid Crystal Gratings. Adv. Mater. 2019, 31, 1806172. [Google Scholar] [CrossRef]
- Chen, R.; Lee, Y.; Zhan, T.; Yin, K.; An, Z.; Wu, S. Multistimuli-responsive self-organized liquid crystal Bragg gratings. Adv. Opt. Mater. 2019, 7, 1900101. [Google Scholar] [CrossRef]
- Algorri, J.F.; Morawiak, P.; Zografopoulos, D.C.; Bennis, N.; Spadlo, A.; Rodríguez-Cobo, L.; Jaroszewicz, L.R.; Sánchez-Pena, J.M.; López-Higuera, J.M. Multifunctional light beam control device by stimuli-responsive liquid crystal micro-grating struc-tures. Sci. Rep. 2020, 10, 13806. [Google Scholar] [CrossRef]
- Muravsky, A.; Agabekov, V.; Zhavnerko, G.; Mahilny, U.; Stankevich, A. P-123: Patterned Rubbing Alignment Technology. SID Symp. Dig. Tech. Pap. 2010, 41, 1727–1730. [Google Scholar] [CrossRef]
- Chen, J.; Bos, P.J.; Vithana, H.; Johnson, D.L. An electro-optically controlled liquid crystal diffraction grating. Appl. Phys. Lett. 1995, 67, 2588–2590. [Google Scholar] [CrossRef]
- Rutkowska, K.; Chychłowski, M.; Kwasny, M.; Ostromęcka, I.; Piłka, J.; Laudyn, U.A. Light propagation in periodic photonic structures formed by photo-orientation and photo-polymerization of nematic liquid crystals. Opto-Electron. Rev. 2017, 25, 118–126. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, Y.-C.; Ge, Y.-H.; Jiang, R.-G.; Wang, X.-Z.; Li, S.-S.; Chen, L.-J. Photoalignment of dye-doped cholesteric liquid crystals for electrically tunable patterns with fingerprint textures. Opt. Express 2018, 26, 1422–1432. [Google Scholar] [CrossRef]
- Chigrinov, V.; Kozenkov, V.M.; Kwok, H.-S. Photoalignment of Liquid Crystalline Materials; Wiley-SID Series in Display Technology; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pan, S.; Ho, J.Y.-L.; Chigrinov, V.G.; Kwok, H.S. Novel Photoalignment Method Based on Low-Molecular-Weight Azobenzene Dyes and Its Application for High-Dichroic-Ratio Polarizers. ACS Appl. Mater. Interfaces 2018, 10, 9032–9037. [Google Scholar] [CrossRef]
- Ji, W.; Wei, B.-Y.; Chen, P.; Hu, W.; Lu, Y.-Q. Optical field control via liquid crystal photoalignment. Mol. Cryst. Liq. Cryst. 2017, 644, 3–11. [Google Scholar] [CrossRef]
- Harper, C.A. Modern Plastics Handbook; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Castellano, J.A. Liquid Gold—The Story of Liquid Crystal Displays and the Creation of an Industry; World Scientific Publishing Company: Covent Garden, London, UK, 2005. [Google Scholar]
- Yang, D.-K.; Wu, S.-T. Fundamentals of Liquid Crystal Devices; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 1993. [Google Scholar]
- Vicari, L. Optical Applications of Liquid Crystals; Taylor & Francis: Oxfordshire, UK, 2003. [Google Scholar]
- Sebastián, N.; Osterman, N.; Lisjak, D.; Čopič, M.; Mertelj, A. Director reorientation dynamics of ferromagnetic nematic liquid crystals. Soft Matter 2018, 14, 7180–7189. [Google Scholar] [CrossRef] [Green Version]
- Stewart, I.W. The Static and Dynamic Continuum Theory of Liquid Crystals: A Mathematical Introduction; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Bošnjaković, D.; Sebastián, N.; Drevenšek-Olenik, I. Magnetically Tunable Liquid Crystal-Based Optical Diffraction Gratings. Polymers 2020, 12, 2355. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Kogelnik, H. Coupled Wave Theory for Thick Hologram Gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K.; Grann, E.B.; Pommet, D.A. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Fleisch, M.; Gao, S.; Bošnjaković, D.; Zhang, X.; Rupp, R.A.; Drevenšek-Olenik, I. Laser-written polymeric scaffolds for micro-patterned liquid crystal alignment. Liq. Cryst. 2019, 46, 2075–2084. [Google Scholar] [CrossRef]
- MicroChem. SU-8 3000 Data Sheet. Available online: http://microchem.com/pdf/SU8%203000%20Data%20Sheet.pdf (accessed on 24 May 2021).
- Zhang, X.; Xu, J.; Li, W.; Drevensek-olenik, I.; Cui, W.; Shi, B.; Wang, Z.; Wu, Q.; Kong, Y. Micro/Nano Region Liquid Crystal Alignment Method and System Thereof Based on Laser Direct Writing. Nankai University. CN Patent 148,861,651, 5 September 2018. [Google Scholar]
- Zhou, X.; Hou, Y.; Lin, J. A review on the processing accuracy of two-photon polymerization. AIP Adv. 2015, 5, 030701. [Google Scholar] [CrossRef]
- Lee, C.H.; Yoshida, H.; Miura, Y.; Fujii, A.; Ozaki, M. Local liquid crystal alignment on patterned micrograting structures photofabricated by two photon excitation direct laser writing. Appl. Phys. Lett. 2008, 93, 173509. [Google Scholar] [CrossRef]
- Ji, Z.; Zhang, X.; Shi, B.; Li, W.; Luo, W.; Drevensek-Olenik, I.; Wu, Q.; Xu, J. Compartmentalized liquid crystal alignment induced by sparse polymer ribbons with surface relief gratings. Opt. Lett. 2016, 41, 336–339. [Google Scholar] [CrossRef]
- Kitson, S.; Geisow, A. Controllable alignment of nematic liquid crystals around microscopic posts: Stabilization of multiple states. Appl. Phys. Lett. 2002, 80, 3635–3637. [Google Scholar] [CrossRef]
- Kitson, S.C.; Edwards, E.G.; Geisow, A.D. Designing liquid crystal alignment surfaces. Appl. Phys. Lett. 2008, 92, 073503. [Google Scholar] [CrossRef]
- Ji, Z.; Zhang, X.; Zhang, Y.; Wang, Z.; Drevensek-Olenik, I.; Rupp, R.A.; Li, W.; Wu, Q.; Xu, J. Electrically tunable generation of vectorial vortex beams with micro-patterned liquid crystal structures. Chin. Opt. Lett. 2017, 15, 070501. [Google Scholar]
- Berreman, D.W. Alignment of liquid crystals by grooved surfaces. Mol. Cryst. Liq. Cryst. 1973, 23, 215–231. [Google Scholar] [CrossRef]
- Frank, F.C.I. Liquid crystals. On the theory of liquid crystals. Discuss. Faraday Soc. 1958, 25, 19. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, R.; Zhu, J.; Wu, S.-T. A simple method to measure the twist elastic constant of a nematic liquid crystal. Liq. Cryst. 2015, 42, 1738–1742. [Google Scholar] [CrossRef]
- Li, J.; Wen, C.H.; Gauza, S.; Lu, R.; Wu, S.T. Refractive Indices of Liquid Crystals for Display Applications. J. Disp. Technol. 2005, 1, 51–61. [Google Scholar] [CrossRef]
- Rapini, A.; Papoular, M. Distorsion D’une Lamelle Nématique Sous Champ Magnétique Conditions D’ancrage Aux Parois. J. Phys. Coll. 1969, 30, 54–56. [Google Scholar] [CrossRef]
- Napoli, G. Weak anchoring effects in electrically driven Freedericksz transitions. J. Phys. A Math. Gen. 2006, 39, 11–31. [Google Scholar] [CrossRef]
- Costa Pereira, A.E.; Rosato, A. Transmission of Nematic Liquid Crystals in Electric Fields. Rev. Bras. Fis. 1975, 5, 237–241. [Google Scholar]
- Gaylord, T.K.; Moharam, M.G. Analysis and applications of optical diffraction by gratings. Proc. IEEE 1985, 73, 894. [Google Scholar] [CrossRef]
- Introduction to S4—S4 1.1 Documentation. Available online: https://web.stanford.edu/group/fan/S4/ (accessed on 23 June 2021).
- Solodar, A.; Cerkauskaite, A.; Drevinskas, R.; Kazansky, P.G.; Abdulhalim, I. Ultrafast laser induced nanostructured ITO for liquid crystal alignment and higher transparency electrodes. Appl. Phys. Lett. 2018, 113, 081603. [Google Scholar] [CrossRef]
- Li, L. Use of Fourier series in the analysis of discontinuous periodic structures. J. Opt. Soc. Am. A 1996, 13, 1870–1876. [Google Scholar] [CrossRef]
- Popov, E.; Neviere, M.; Gralak, B.; Tayeb, G. Staircase approximation validity for arbitrary-shaped gratings. J. Opt. Soc. Am. A 2002, 19, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Mertelj, A.; Lisjak, D. Ferromagnetic nematic liquid crystals. Liq. Cryst. Rev. 2017, 5, 1–33. [Google Scholar] [CrossRef]
- Tsakonas, C.; Davidson, A.J.; Brown, C.V.; Mottram, N.J. Multistable alignment states in nematic liquid crystal filled wells. Appl. Phys. Lett. 2007, 90, 111913. [Google Scholar] [CrossRef]
- Walton, J.; Mottram, N.J.; McKay, G. Nematic liquid crystal director structures in rectangular regions. Phys. Rev. E. 2018, 97, 022702. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A.; Lewis, A. Multistable nematic wells: Modelling perspectives, recent results and new directions. Liq Cryst. 2016, 43, 2332–2351. [Google Scholar] [CrossRef] [Green Version]
- Migara, L.K.; Song, J.K. Standing wave-mediated molecular reorientation and spontaneous formation of tunable, concentric defect arrays in liquid crystal cells. NPG Asia Mater. 2018, 10, 1–8. [Google Scholar] [CrossRef] [Green Version]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bošnjaković, D.; Fleisch, M.; Zhang, X.; Drevenšek-Olenik, I. Electrically Tuneable Optical Diffraction Gratings Based on a Polymer Scaffold Filled with a Nematic Liquid Crystal. Polymers 2021, 13, 2292. https://doi.org/10.3390/polym13142292
Bošnjaković D, Fleisch M, Zhang X, Drevenšek-Olenik I. Electrically Tuneable Optical Diffraction Gratings Based on a Polymer Scaffold Filled with a Nematic Liquid Crystal. Polymers. 2021; 13(14):2292. https://doi.org/10.3390/polym13142292
Chicago/Turabian StyleBošnjaković, Dejan, Mathias Fleisch, Xinzheng Zhang, and Irena Drevenšek-Olenik. 2021. "Electrically Tuneable Optical Diffraction Gratings Based on a Polymer Scaffold Filled with a Nematic Liquid Crystal" Polymers 13, no. 14: 2292. https://doi.org/10.3390/polym13142292
APA StyleBošnjaković, D., Fleisch, M., Zhang, X., & Drevenšek-Olenik, I. (2021). Electrically Tuneable Optical Diffraction Gratings Based on a Polymer Scaffold Filled with a Nematic Liquid Crystal. Polymers, 13(14), 2292. https://doi.org/10.3390/polym13142292