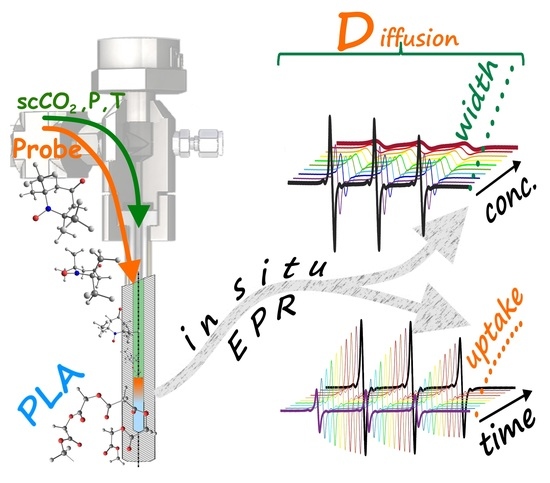
Solute Diffusion into Polymer Swollen by Supercritical CO2 by High-Pressure Electron Paramagnetic Resonance Spectroscopy and Chromatography
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Measurement of Equilibrium Distribution between Polymer and scCO2 Using Supercritical Chromatography
2.3. Measurement of Polymer Impregnation Kinetics Using EPR Spectroscopy
2.4. Measurement of Concentration Broadening of EPR Spectra
3. Results and Discussion
3.1. TEMPONE Uptake Measurement
3.2. TEMPONE EPR Concentration Broadening Measurement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berens, A.R.; Huvard, G.S.; Korsmeyer, R.W.; Kunig, F.W. Application of compressed carbon dioxide in the incorporation of additives into polymers. J. Appl. Polym. Sci. 1992, 46, 231–242. [Google Scholar] [CrossRef]
- Sand, M.L. Method for Impregnating a Thermoplastic Polymer. EP0200197A3, 22 June 1986. [Google Scholar]
- Champeau, M.; Thomassin, J.-M.; Tassaing, T.; Jérôme, C. Drug loading of polymer implants by supercritical CO2 assisted impregnation: A review. J. Control. Release 2015, 209, 248–259. [Google Scholar] [CrossRef]
- Guney, O.; Akgerman, A. Synthesis of controlled-release products in supercritical medium. AIChE J. 2002, 48, 856–866. [Google Scholar] [CrossRef]
- Kankala, R.K.; Zhang, Y.S.; Wang, S.-B.; Lee, C.-H.; Chen, A.-Z. Supercritical Fluid Technology: An Emphasis on Drug Delivery and Related Biomedical Applications. Adv. Healthc. Mater. 2017, 6, 1700433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rojas, A.; Torres, A.; José Galotto, M.; Guarda, A.; Julio, R. Supercritical impregnation for food applications: A review of the effect of the operational variables on the active compound loading. Crit. Rev. Food Sci. Nutr. 2020, 60, 1290–1301. [Google Scholar] [CrossRef] [PubMed]
- Rojas, A.; Torres, A.; Añazco, A.; Villegas, C.; Galotto, M.J.; Guarda, A.; Romero, J. Effect of pressure and time on scCO2-assisted incorporation of thymol into LDPE-based nanocomposites for active food packaging. J. CO2 Util. 2018, 26, 434–444. [Google Scholar] [CrossRef]
- Saus, W.; Knittel, D.; Schollmeyer, E. Dyeing of Textiles in Supercritical Carbon Dioxide. Text. Res. J. 1993, 63, 135–142. [Google Scholar] [CrossRef]
- Bach, E.; Cleve, E.; Schollmeyer, E. Dyeing of poly(ethylene terephthalate) fibers in supercritical carbon dioxide. In Process Technology Proceedings; Elsevier: Amsterdam, The Netherlands, 1996; pp. 581–586. [Google Scholar]
- Kazarian, S.G.; Brantley, N.H.; West, B.L.; Vincent, M.F.; Eckert, C.A. In situ spectroscopy of polymers subjected to supercritical CO2: Plasticization and dye impregnation. Appl. Spectrosc. 1997, 51, 491–494. [Google Scholar] [CrossRef]
- Ngo, T.T.; Liotta, C.L.; Eckert, C.A.; Kazarian, S.G. Supercritical fluid impregnation of different azo-dyes into polymer: In situ UV/Vis spectroscopic study. J. Supercrit. Fluids 2003, 27, 215–221. [Google Scholar] [CrossRef]
- Sicardi, S.; Manna, L.; Banchero, M. Comparison of dye diffusion in poly(ethylene terephthalate) films in the presence of a supercritical or aqueous solvent. Ind. Eng. Chem. Res. 2000, 39, 4707–4713. [Google Scholar] [CrossRef]
- Banchero, M. Recent advances in supercritical fluid dyeing. Color. Technol. 2020, 136, 317–335. [Google Scholar] [CrossRef]
- Rosolovsky, J.; Boggess, R.K.; Rubira, A.F.; Taylor, L.T.; Stoakley, D.M.; St. Clair, A.K. Supercritical fluid infusion of silver into polyimide films of varying chemical composition. J. Mater. Res. 1997, 12, 3127–3133. [Google Scholar] [CrossRef]
- Boggess, R.K.; Taylor, L.T.; Stoakley, D.M.; St. Clair, A.K. Highly reflective polyimide films created by supercritical fluid infusion of a silver additive. J. Appl. Polym. Sci. 1997, 64, 1309–1317. [Google Scholar] [CrossRef]
- Watkins, J.J.; McCarthy, T.J. Polymer/Metal Nanocomposite Synthesis in Supercritical CO2. Chem. Mater. 1995, 7, 1991–1994. [Google Scholar] [CrossRef]
- Siril, P.F.; Türk, M. Synthesis of Metal Nanostructures Using Supercritical Carbon Dioxide: A Green and Upscalable Process. Small 2020, 16, 2001972. [Google Scholar] [CrossRef]
- Watkins, J.J.; McCarthy, T.J. Polymerization in Supercritical Fluid-Swollen Polymers: A New Route to Polymer Blends. Macromolecules 1994, 27, 4845–4847. [Google Scholar] [CrossRef]
- Kung, E.; Lesser, A.J.; McCarthy, T.J. Morphology and Mechanical Performance of Polystyrene/Polyethylene Composites Prepared in Supercritical Carbon Dioxide. Macromolecules 1998, 31, 4160–4169. [Google Scholar] [CrossRef]
- Cooper, A.I. Polymer synthesis and processing using supercritical carbon dioxide. J. Mater. Chem. 2000, 10, 207–234. [Google Scholar] [CrossRef]
- Girard, E.; Tassaing, T.; Marty, J.D.; Destarac, M. Structure-Property Relationships in CO2-philic (Co)polymers: Phase Behavior, Self-Assembly, and Stabilization of Water/CO2 Emulsions. Chem. Rev. 2016, 116, 4125–4169. [Google Scholar] [CrossRef]
- Tomasko, D.L.; Li, H.; Liu, D.; Han, X.; Wingert, M.J.; Lee, L.J.; Koelling, K.W. A Review of CO2 Applications in the Processing of Polymers. Ind. Eng. Chem. Res. 2003, 42, 6431–6456. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, C.; Tomasko, D. Confocal microscopy analysis of supercritical fluid impregnation of polypropylene. Ind. Eng. Chem. Res. 2002, 41, 1780–1786. [Google Scholar] [CrossRef]
- Chumakova, N.A.; Golubeva, E.N.; Ivanova, T.A.; Vorobieva, N.N.; Timashev, P.S.; Bagratashvili, V.N. EPR Diagnostics of D,L-Polylactide Porous Matrices Formed in Supercritical CO2. Russ. J. Phys. Chem. B 2018, 12, 1255–1260. [Google Scholar] [CrossRef]
- Westrin, B.A.; Axelsson, A.; Zacchi, G. Diffusion measurement in gels. J. Control. Release 1994, 30, 189–199. [Google Scholar] [CrossRef]
- Zoski, C.G. (Ed.) Handbook of Electrochemistry; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 9780444519580. [Google Scholar]
- Price, W.S. NMR Studies of Translational Motion; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780511770487. [Google Scholar]
- Thurecht, K.J.; Hill, D.J.T.; Whittaker, A.K. NMR Microscopy: A Tool for Measuring Monomer Diffusion in Supercritical CO2. Macromol. Chem. Phys. 2006, 207, 1539–1545. [Google Scholar] [CrossRef]
- Hornak, J.P.; Moscicki, J.K.; Schneider, D.J.; Freed, J.H. Diffusion coefficients in anisotropic fluids by ESR imaging of concentration profiles. J. Chem. Phys. 1986, 84, 3387–3395. [Google Scholar] [CrossRef]
- Molin, Y.N.; Salikhov, K.M.; Zamaraev, K.I. Spin Exchange; Springer: Berlin/Heidelberg, Germany, 1980; ISBN 978-3-642-67668-0. [Google Scholar]
- Fleming, O.S.; Stepanek, F.; Kazarian, S.G. Dye diffusion in polymer films subjected to supercritical CO2: Confocal raman microscopy and modelling. Macromol. Chem. Phys. 2005, 206, 1077–1083. [Google Scholar] [CrossRef]
- Fleming, O.S.; Kazarian, S.G.; Bach, E.; Schollmeyer, E. Confocal Raman study of poly(ethylene terephthalate) fibres dyed in supercritical carbon dioxide: Dye diffusion and polymer morphology. Polymer 2005, 46, 2943–2949. [Google Scholar] [CrossRef]
- Naddaf, A.A.; Bart, H.J. Raman Spectroscopy: Mutual Diffusion Coefficient in Hydrogels. Defect Diffus. Forum 2011, 312–315, 193–198. [Google Scholar] [CrossRef]
- Dirauf, M.P.; Hajnal, A.; Gurikov, P.; Braeuer, A.S. Protein gel shrinkage during solvent exchange: Quantification of gel compaction, mass transfer and compressive strength. Food Hydrocoll. 2021, 120, 106916. [Google Scholar] [CrossRef]
- Huang, W.J.; Frick, T.S.; Landry, M.R.; Lee, J.A.; Lodge, T.P.; Tirrell, M. Tracer diffusion measurement in polymer solutions near the glass transition by forced rayleigh scattering. AIChE J. 1987, 33, 573–582. [Google Scholar] [CrossRef]
- Ehlich, D.; Sillescu, H. Tracer diffusion at the glass transition. Macromolecules 1990, 23, 1600–1610. [Google Scholar] [CrossRef]
- Sicardi, S.; Manna, L.; Banchero, M. Diffusion of disperse dyes in PET films during impregnation with a supercritical fluid. J. Supercrit. Fluids 2000, 17, 187–194. [Google Scholar] [CrossRef]
- von Schnitzler, J.; Eggers, R. Mass transfer in polymers in a supercritical CO2-atmosphere. J. Supercrit. Fluids 1999, 16, 81–92. [Google Scholar] [CrossRef]
- Champeau, M.; Coutinho, I.T.; Thomassin, J.M.; Tassaing, T.; Jérôme, C. Tuning the release profile of ketoprofen from poly(L-lactic acid) suture using supercritical CO2 impregnation process. J. Drug Deliv. Sci. Technol. 2020, 55, 101468. [Google Scholar] [CrossRef]
- Alsoy, S.; Duda, J.L. Supercritical devolatilization of polymers. AIChE J. 1998, 44, 582–590. [Google Scholar] [CrossRef]
- Alsoy, S.; Duda, J.L. Processing of Polymers with Supercritical Fluids. Chem. Eng. Technol. 1999, 22, 971. [Google Scholar] [CrossRef]
- Kazarian, S.G.; Martirosyan, G.G. Spectroscopy of polymer/drug formulations processed with supercritical fluids: In situ ATR-IR and Raman study of impregnation of ibuprofen into PVP. Int. J. Pharm. 2002, 232, 81–90. [Google Scholar] [CrossRef]
- Vincent, M.F.; Kazarian, S.G.; Eckert, C.A. “ Tunable ” Diffusion of D2O in CO2-Swollen Poly(Methyl Methacrylate) Films. J. Supercrit. Fluids 1997, 49, 127–135. [Google Scholar] [CrossRef]
- Champeau, M.; Thomassin, J.M.; Jérôme, C.; Tassaing, T. In situ investigation of supercritical CO2 assisted impregnation of drugs into a polymer by high pressure FTIR micro-spectroscopy. Analyst 2015, 140, 869–879. [Google Scholar] [CrossRef]
- Kazarian, S.G.; Vincent, M.F.; West, B.L.; Eckert, C.A. Partitioning of solutes and cosolvents between supercritical CO2 and polymer phases. J. Supercrit. Fluids 1998, 13, 107–112. [Google Scholar] [CrossRef]
- Chapman, B.R.; Gochanour, C.R.; Paulaitis, M.E. CO2-Enhanced Diffusion of Azobenzene in Glassy Polystyrene near the Glass Transition. Macromolecules 1996, 29, 5635–5649. [Google Scholar] [CrossRef]
- Schlick, S. Advanced ESR Methods in Polymer Research; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; ISBN 9780471731894. [Google Scholar]
- Connon, C.S.; Falk, R.F.; Randolph, T.W. Role of Crystallinity in Retention of Polymer Particle Morphology in the Presence of Compressed Carbon Dioxide. Macromolecules 1999, 32, 1890–1896. [Google Scholar] [CrossRef]
- Harbron, E.J.; Bunyard, W.C.; Forbes, M.D.E. Electron paramagnetic resonance spin probe study of carbon dioxide-induced polymer plasticization. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 2097–2108. [Google Scholar] [CrossRef]
- Wessig, M.; Spitzbarth, M.; Drescher, M.; Winter, R.; Polarz, S. Multiple scale investigation of molecular diffusion inside functionalized porous hosts using a combination of magnetic resonance methods. Phys. Chem. Chem. Phys. 2015, 17, 15976–15988. [Google Scholar] [CrossRef] [Green Version]
- Alekseev, E.S.; Alentiev, A.Y.; Belova, A.S.; Bogdan, V.I.; Bogdan, T.V.; Bystrova, A.V.; Gafarova, E.R.; Golubeva, E.N.; Grebenik, E.A.; Gromov, O.I.; et al. Supercritical fluids in chemistry. Russ. Chem. Rev. 2020, 89, 1337. [Google Scholar] [CrossRef]
- Ganapathy, S.; Carlier, C.; Randolph, T.W.; O’Brien, J.A. Influence of Local Structural Correlations on Free-Radical Reactions in Supercritical Fluids: A Hierarchical Approach. Ind. Eng. Chem. Res. 1996, 35, 19–27. [Google Scholar] [CrossRef]
- Carlier, C.; Randolph, T.W. Dense-gas solvent-solute clusters at near-infinite dilution: EPR spectroscopic evidence. AIChE J. 1993, 39, 876–884. [Google Scholar] [CrossRef]
- Tachikawa, T.; Akiyama, K.; Yokoyama, C.; Tero-Kubota, S. Local density effects on the hyperfine splitting constant and line width of TEMPO radical in gaseous and supercritical carbon dioxide. Chem. Phys. Lett. 2003, 376, 350–357. [Google Scholar] [CrossRef]
- deGrazia, J.L.; Randolph, T.W.; O’Brien, J.A. Rotational Relaxation in Supercritical Carbon Dioxide Revisited: A Study of Solute-Induced Local Density Augmentation. J. Phys. Chem. A 1998, 102, 1674–1681. [Google Scholar] [CrossRef]
- Batchelor, S.N. Free Radical Motion in Super Critical Fluids Probed by EPR Spectroscopy. J. Phys. Chem. B 1998, 102, 615–619. [Google Scholar] [CrossRef]
- Randolph, T.W.; Carlier, C. Free-radical reactions in supercritical ethane: A probe of supercritical fluid structure. J. Phys. Chem. 1992, 96, 5146–5151. [Google Scholar] [CrossRef]
- Trukhan, S.N.; Yudanov, V.F.; Mart’yanov, O.N. The effect of clustering of VO2+ ions in sub- and supercritical water. An in situ EPR study. Russ. J. Phys. Chem. B 2013, 7, 924–931. [Google Scholar] [CrossRef]
- Trukhan, S.N.; Yudanov, V.F.; Martyanov, O.N. Electron spin resonance of VO2+ radical-ion in sub- and supercritical water. J. Supercrit. Fluids 2011, 57, 247–250. [Google Scholar] [CrossRef]
- Randolph, T.W.; Clark, D.S.; Blanch, H.W.; Prausnitz, J.M. Cholesterol aggregation and interaction with cholesterol oxidase in supercritical carbon dioxide. Proc. Natl. Acad. Sci. USA 1988, 85, 2979–2983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Randolph, T.W.; Clark, D.S.; Blanch, H.W.; Prausnitz, J.M. Enzymatic Oxidation of Cholesterol Aggregates in Supercritical Carbon Dioxide. Science 1988, 239, 387–390. [Google Scholar] [CrossRef]
- Miller, D.A.; Clark, D.S.; Blanch, H.W.; Prausnitz, J.M. Fatty acid aggregation in supercritical carbon dioxide. J. Supercrit. Fluids 1991, 4, 124–126. [Google Scholar] [CrossRef]
- Johnston, K.P.; Harrison, K.L.; Clarke, M.J.; Howdle, S.M.; Heitz, M.P.; Bright, F.V.; Carlier, C.; Randolph, T.W. Water-in-Carbon Dioxide Microemulsions: An Environment for Hydrophiles Including Proteins. Science 1996, 271, 624–626. [Google Scholar] [CrossRef]
- Heitz, M.P.; Carlier, C.; DeGrazia, J.; Harrison, K.L.; Johnston, K.P.; Randolph, T.W.; Bright, F. V Water Core within Perfluoropolyether-Based Microemulsions Formed in Supercritical Carbon Dioxide. J. Phys. Chem. B 1997, 101, 6707–6714. [Google Scholar] [CrossRef]
- Kopylov, A.S.; Radtsig, V.A.; Glagolev, N.N.; Solovieva, A.B.; Bagratashvili, V.N. SCF impregnation of polymer matrices with stable nitroxyl radicals. Russ. J. Phys. Chem. B 2015, 9, 998–1004. [Google Scholar] [CrossRef]
- Golubeva, E.N.; Gromov, O.I.; Chumakova, N.A.; Feklichev, E.D.; Mel’nikov, M.Y.; Bagratashvili, V.N. Impregnation of polymers with 2,2,6,6-tetramethyl-4-oxo-piperidine-1-oxyl (TEMPONE) paramagnetic probe in sub- and supercritical CO2. Russ. J. Phys. Chem. B 2016, 10, 1229–1236. [Google Scholar] [CrossRef]
- Golubeva, E.N.; Chumakova, N.A.; Kuzin, S.V.; Grigoriev, I.A.; Kalai, T.; Korotkevich, A.A.; Bogorodsky, S.E.; Krotova, L.I.; Popov, V.K.; Lunin, V.V. Paramagnetic bioactives encapsulated in poly(D,L-lactide) microparticules: Spatial distribution and in vitro release kinetics. J. Supercrit. Fluids 2020, 158, 104748. [Google Scholar] [CrossRef]
- Chumakova, N.A.; Golubeva, E.N.; Kuzin, S.V.; Ivanova, T.A.; Grigoriev, I.A.; Kostjuk, S.V.; Melnikov, M.Y. New Insight into the Mechanism of Drug Release from Poly(d,l-lactide) Film by Electron Paramagnetic Resonance. Polymers 2020, 12, 3046. [Google Scholar] [CrossRef]
- Peper, S.; Dohrn, R. Sampling from fluid mixtures under high pressure: Review, case study and evaluation. J. Supercrit. Fluids 2012, 66, 2–15. [Google Scholar] [CrossRef]
- Yamini, Y.; Bahramifar, N. Solubility of Polycyclic Aromatic Hydrocarbons in Supercritical Carbon Dioxide. J. Chem. Eng. Data 2000, 45, 53–56. [Google Scholar] [CrossRef]
- Li, B.; Guo, W.; Ramsey, E.D. Determining phenol partition coefficient values in water- and industrial process water-supercritical CO2 systems using direct aqueous SFE apparatus simultaneously interfaced with on-line SFC and on-line HPLC. J. Supercrit. Fluids 2019, 152, 104558. [Google Scholar] [CrossRef]
- Poliakoff, M.; Howdle, S.M.; Kazarian, S.G. Vibrational Spectroscopy in Supercritical Fluids: From Analysis and Hydrogen Bonding to Polymers and Synthesis. Angew. Chem. Int. Ed. Engl. 1995, 34, 1275–1295. [Google Scholar] [CrossRef]
- Suzuki, S.; Aoki, K.; Moribe, K.; Sako, T. Solubility measurement in supercritical CO2 with high pressure UV/VIS absorption spectroscopy. In Asian Pacific Confederation of Chemical Engineering Congress Program and Abstract; The Society of Chemical Engineers: Tokyo, Japan, 2004; p. 839. [Google Scholar]
- Carrott, M.J.; Wai, C.M. UV−Visible Spectroscopic Measurement of Solubilities in Supercritical CO2 Using High-Pressure Fiber-Optic Cells. Anal. Chem. 1998, 70, 2421–2425. [Google Scholar] [CrossRef]
- Stewart, S.; Domínguez-Robles, J.; Donnelly, R.; Larrañeta, E. Implantable Polymeric Drug Delivery Devices: Classification, Manufacture, Materials, and Clinical Applications. Polymers 2018, 10, 1379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scoponi, G.; Guzman-Puyol, S.; Caputo, G.; Ceseracciu, L.; Athanassiou, A.; Heredia-Guerrero, J.A. Highly biodegradable, ductile all-polylactide blends. Polymer (Guildf.) 2020, 193, 122371. [Google Scholar] [CrossRef]
- Ju, J.; Peng, X.; Huang, K.; Li, L.; Liu, X.; Chitrakar, C.; Chang, L.; Gu, Z.; Kuang, T. High-performance porous PLLA-based scaffolds for bone tissue engineering: Preparation, characterization, and in vitro and in vivo evaluation. Polymer (Guildf.) 2019, 180, 121707. [Google Scholar] [CrossRef]
- Mironov, A.V.; Mironova, O.A.; Syachina, M.A.; Popov, V.K. 3D printing of polylactic-co-glycolic acid fiber scaffolds using an antisolvent phase separation process. Polymer (Guildf.) 2019, 182, 121845. [Google Scholar] [CrossRef]
- Kostenko, M.O.; Ustinovich, K.B.; Pokrovskii, O.I. Online Monitoring of Adsorption onto Silica Xerogels and Aerogels from Supercritical Solutions Using Supercritical Fluid Chromatography. Russ. J. Inorg. Chem. 2020, 65, 1577–1584. [Google Scholar] [CrossRef]
- Johannsen, M.; Brunner, G. Solubilities of the xanthines caffeine, theophylline and theobromine in supercritical carbon dioxide. Fluid Phase Equilib. 1994, 95, 215–226. [Google Scholar] [CrossRef]
- Li, B.; Guo, W.; Song, W.; Ramsey, E.D. Determining the Solubility of Organic Compounds in Supercritical Carbon Dioxide Using Supercritical Fluid Chromatography Directly Interfaced to Supercritical Fluid Solubility Apparatus. J. Chem. Eng. Data 2016, 61, 2128–2134. [Google Scholar] [CrossRef]
- Minaev, N.V.; Gromov, O.I.; Golubeva, E.N.; Vorobiev, A.K.; Bagratashvili, V.N. High-Pressure Reactor for Registration of Electron Paramagnetic Resonance Spectra in Supercritical Carbon Dioxide. Prib. Tech. Exp. 2019, 62, 151–153. (In Russian) [Google Scholar] [CrossRef]
- Wallen, S.L.; Schoenbachler, L.K.; Dawson, E.D.; Blatchford, M.A. A Polymer NMR Cell for the Study of High-Pressure and Supercritical Fluid Solutions. Anal. Chem. 2000, 72, 4230–4234. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical Properties of Fluid Systems. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2021. [Google Scholar]
- Span, R.; Wagner, W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Tomasko, D.L. Carbon dioxide sorption and dilation of poly(lactide-co-glycolide). J. Supercrit. Fluids 2007, 39, 416–425. [Google Scholar] [CrossRef]
- Aionicesei, E.; Škerget, M.; Knez, Ž. Measurement of CO2 solubility and diffusivity in poly(l-lactide) and poly(d,l-lactide-co-glycolide) by magnetic suspension balance. J. Supercrit. Fluids 2008, 47, 296–301. [Google Scholar] [CrossRef]
- Milovanović, S.L.; Kuska, R.M.; Škorić-Lučić, M.L.; Kalagasidis-Krušić, M.T.; Frerich, S.; Žižović, I.T.; Ivanović, J.Z. Swelling kinetics and impregnation of PLA with thymol under supercritical CO2 conditions. Tehnika 2016, 71, 16–20. [Google Scholar] [CrossRef] [Green Version]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1975; ISBN 0 19 853344 6. [Google Scholar]
- Nayeem, A.; Rananavare, S.B.; Sastry, V.S.S.; Freed, J.H. Heisenberg spin exchange and molecular diffusion in liquid crystals. J. Chem. Phys. 1989, 91, 6887–6905. [Google Scholar] [CrossRef]
- Mladenova, B.Y.; Chumakova, N.A.; Pergushov, V.I.; Kokorin, A.I.; Grampp, G.; Kattnig, D.R. Rotational and Translational Diffusion of Spin Probes in Room-Temperature Ionic Liquids. J. Phys. Chem. B 2012, 116, 12295–12305. [Google Scholar] [CrossRef] [PubMed]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Sato, H.; Bottle, S.E.; Blinco, J.P.; Micallef, A.S.; Eaton, G.R.; Eaton, S.S. Electron spin–lattice relaxation of nitroxyl radicals in temperature ranges that span glassy solutions to low-viscosity liquids. J. Magn. Reson. 2008, 191, 66–77. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, I.C.; Lacombe, R.H. An elementary equation of state for polymer liquids. J. Polym. Sci. Polym. Lett. Ed. 1977, 15, 71–75. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical Thermodynamics of Polymer Solutions. Macromolecules 1978, 11, 1145–1156. [Google Scholar] [CrossRef] [Green Version]
- Kiran, E.; Xiong, Y.; Zhuang, W. Modeling polyethylene solutions in near and supercritical fluids using the sanchez-lacombe model. J. Supercrit. Fluids 1993, 6, 193–203. [Google Scholar] [CrossRef]
- Xiong, Y.; Kiran, E. Prediction of high-pressure phase behaviour in polyethylene/n-pentane/carbon dioxide ternary system with the Sanchez-Lacombe model. Polymer (Guildf.) 1994, 35, 4408–4415. [Google Scholar] [CrossRef]
- Sato, Y.; Yurugi, M.; Fujiwara, K.; Takishima, S.; Masuoka, H. Solubilities of carbon dioxide and nitrogen in polystyrene under high temperature and pressure. Fluid Phase Equilibria. 1996, 125, 129–138. [Google Scholar] [CrossRef]
- Kurban, M.R. A study of the relation between translational and rotational diffusion through measurement of molecular recollision. J. Chem. Phys. 2011, 134, 034503. [Google Scholar] [CrossRef] [PubMed]
- Salikhov, K.M. New Paradigm of Spin Exchange and its Manifestations in EPR Spectroscopy. Appl. Magn. Reson. 2020, 51, 297–325. [Google Scholar] [CrossRef]
- Spitzbarth, M.; Scherer, A.; Schachtschneider, A.; Imming, P.; Polarz, S.; Drescher, M. Time-, spectral- and spatially resolved EPR spectroscopy enables simultaneous monitoring of diffusion of different guest molecules in nano-pores. J. Magn. Reson. 2017, 283, 45–51. [Google Scholar] [CrossRef] [PubMed]







| T °C | K | Duptake, m2/s | Dlwpp, m2/s | τcorr, s | aiso, G |
|---|---|---|---|---|---|
| 40 | 520 ± 50 | 5 ± 2 × 10−12 | 7 ± 1 × 10−12 | 6.4 × 10−11 | 14.7 |
| 50 | 380 ± 80 | 10 ± 3 × 10−12 | 8 ± 1 × 10−12 | 5.7 × 10−11 | |
| 60 | 280 ± 50 | 10 ± 2 × 10−12 | 8 ± 1 × 10−12 | 5.5 × 10−11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gromov, O.I.; Kostenko, M.O.; Petrunin, A.V.; Popova, A.A.; Parenago, O.O.; Minaev, N.V.; Golubeva, E.N.; Melnikov, M.Y. Solute Diffusion into Polymer Swollen by Supercritical CO2 by High-Pressure Electron Paramagnetic Resonance Spectroscopy and Chromatography. Polymers 2021, 13, 3059. https://doi.org/10.3390/polym13183059
Gromov OI, Kostenko MO, Petrunin AV, Popova AA, Parenago OO, Minaev NV, Golubeva EN, Melnikov MY. Solute Diffusion into Polymer Swollen by Supercritical CO2 by High-Pressure Electron Paramagnetic Resonance Spectroscopy and Chromatography. Polymers. 2021; 13(18):3059. https://doi.org/10.3390/polym13183059
Chicago/Turabian StyleGromov, Oleg I., Mikhail O. Kostenko, Alexander V. Petrunin, Anastasia A. Popova, Olga O. Parenago, Nikita V. Minaev, Elena N. Golubeva, and Mikhail Ya. Melnikov. 2021. "Solute Diffusion into Polymer Swollen by Supercritical CO2 by High-Pressure Electron Paramagnetic Resonance Spectroscopy and Chromatography" Polymers 13, no. 18: 3059. https://doi.org/10.3390/polym13183059
APA StyleGromov, O. I., Kostenko, M. O., Petrunin, A. V., Popova, A. A., Parenago, O. O., Minaev, N. V., Golubeva, E. N., & Melnikov, M. Y. (2021). Solute Diffusion into Polymer Swollen by Supercritical CO2 by High-Pressure Electron Paramagnetic Resonance Spectroscopy and Chromatography. Polymers, 13(18), 3059. https://doi.org/10.3390/polym13183059