Contour Fitting of Fused Filaments Cross-Section Images by Lemniscates of Booth: Application to Viscous Sintering Kinetics Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plasticized Biopolymer and Filament Extrusion
2.2. Sintering Trials
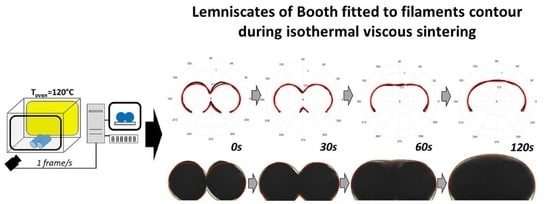
2.3. Morphological Image Analysis
- Step 1: The image of the region of interest (ROI) is cropped in order to focus on the two initial filaments and to follow their progressive sintering, while maintaining the initial coding of the image format as 256 grey levels;
- Step 2: A segmentation is carried out by image thresholding in order to obtain binary images with one white object corresponding to the two filaments (i.e., with pixels = 1) on a black background corresponding to the backlighting (i.e., pixels = 0). The constant lighting conditions allow using a single threshold visually determined to segment the whole images sequence with ImageJ software (free software; National Institutes of Health, Bethesda, MD, USA). Based on each binary image, the morphological image analysis (MIA) is applied to determine each point of the contour of the sintered filaments and to fit the adjusted lemniscate to their contour, according to the following steps:
- Step 3: The identification of the contour pixels by an erosion step on the digital mask corresponding to the filament shape with a 3 × 3 pixels2 structuring element, excluding the oven base;
- Step 4: The determination of the centroid point, i.e., the equivalent of the center of gravity of the white object of the segmented image;
- Step 5: The computation of the maximum horizontal length, Lmax [pixel], from one side to the opposite side of the white object on the binary image;
- Step 6: The fitting of a lemniscate of Booth, adapted to the contour of the filaments on each acquired image, implemented on Matlab® software (The MathWorks Inc., Natick, MA, USA). To carry out this last step, a conversion from the initial image coordinate system to a polar centered one is required (Figure 2b and Figure 3a). Each image is vertically centered on the ordinate at which the horizontal length of the white object is maximum (i.e., where Lmax is determined) and, horizontally, at the abscissa of the centroid, which is equivalent to a central point for the two coalescing filaments.
3. Results
3.1. Successive Lemniscates of Booth to Fit Sintering Sequences
3.2. Determination of the Parameters of the Lemniscate Equations
3.3. Assessment of the Material’s Characteristic Viscous Sintering Time
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turner, B.N.; Strong, R.; Gold, S.A. A review of melt extrusion additive manufacturing processes: I. Process design and modelling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Turner, B.N.; Gold, S.A. A review of melt extrusion additive manufacturing processes: II. Materials, dimensional accuracy, and surface roughness. Rapid Prototyp. J. 2015, 21, 250–261. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Pedersen, D.B.; Spangenberg, J. Numerical simulations of the mesostructure formation in material extrusion additive manufacturing. Addit. Manuf. 2019, 28, 419–429. [Google Scholar] [CrossRef]
- Hopper, R.W. Coalescence of Two Equal Cylinders: Results for Creeping Viscous Plane Flow Driven by Capillarity. J. Am. Cer. Soc. 1984, 67, C262–C264, Erratum in: 1985, 68, C138. [Google Scholar] [CrossRef]
- McIlroy, C.; Olmsted, P.D. Disentanglement effects on welding behaviour of polymer melts during the fused-filament-fabrication method for additive manufacturing. Polymer 2017, 123, 376–391. [Google Scholar] [CrossRef]
- Xin, L.; Boutaous, M.; Xin, S.H.; Siginer, D.A. Multiphysical modeling of the heating phase in the polymer powder bed fusion process. Addit. Manuf. 2017, 18, 121–135. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Vlachopoulos, J. The role of heating and cooling in viscous sintering of pairs of spheres and pairs of cylinders. Rapid Prototyp. J. 2020, 26, 719–726. [Google Scholar] [CrossRef]
- Bellehumeur, C.; Li, L.; Sun, Q.; Gu, P. Modeling of bond formation between polymer filaments in the fused deposition modeling process. J. Manuf. Process 2004, 6, 170–178. [Google Scholar] [CrossRef]
- Boyd, J.; West, W.T.J.; Wu, S.; Takacs, E.S.; Vlachopoulos, J.; Thompson, M.R. Automated image analysis to characterize the melt densification stage of polymer sintering processes. Polym. Test. 2017, 60, 242–249. [Google Scholar] [CrossRef]
- Bakrani Balani, S.; Chabert, F.; Nassiet, V.; Cantarel, A.; Garnier, C. Toward improvement of the properties of parts manufactured by FFF (Fused Filament Fabrication) through understanding the influence of temperature and rheological behaviour on the coalescence phenomenon. AIP Conf. Proc. 2017, 1896, 040008. [Google Scholar] [CrossRef]
- Bakrani Balani, S.; Cantarel, A.; Chabert, F.; Nassiet, V. Influence of parameters controlling the extrusion step in fused filament fabrication (FFF) process applied to polymers using numerical simulation. AIP Conf. Proc. 2018, 1960, 140003. [Google Scholar] [CrossRef]
- Chaunier, L.; Della Valle, G.; Lourdin, D.; Réguerre, A.-L.; Cochet, K.; Leroy, E. Viscous sintering kinetics of biopolymer filaments extruded for 3D printing. Polym. Test. 2019, 77, 105873. [Google Scholar] [CrossRef]
- Chaunier, L.; Guessasma, S.; Belhabib, S.; Della Valle, G.; Lourdin, D.; Leroy, E. Material extrusion of plant biopolymers: Opportunities & challenges for 3D printing. Addit. Manuf. 2018, 21, 220–233. [Google Scholar] [CrossRef]
- Hopper, R.W. Coalescence of 2 viscous cylinders by capillarity. 1. Theory. J. Am. Cer. Soc. 1993, 76, 2947–2952. [Google Scholar] [CrossRef]
- Hopper, R.W. Coalescence of 2 viscous cylinders by capillarity. 2. Shape evolution. J. Am. Cer. Soc. 1993, 76, 2953–2960. [Google Scholar] [CrossRef]
- Frenkel, J. Viscous flow of crystalline bodies under the action of surface tension. J. Phys. (USSR) 1945, 9, 385–391. [Google Scholar]
- Pokluda, O.; Bellehumeur, C.T.; Vlachopoulos, J. Modification of Frenkel’s model for sintering. J. Am. Inst. Chem. Eng. 1997, 43, 3253–3256. [Google Scholar] [CrossRef]
- Bordère, S.; Gendron, D.; Heintz, J.M.; Bernard, D. Monte Carlo prediction of non-Newtonian viscous sintering: Experimental validation for the two-glass-cylinder system. J. Am. Cer. Soc. 2005, 88, 2071–2078. [Google Scholar] [CrossRef]
- Sowinski, K.; Jasion, P. Strength and stability of shells based on Booth lemniscate loaded with external pressure. Thin-Wall. Struct. 2019, 144, 106284. [Google Scholar] [CrossRef]
- Chaunier, L.; Réguerre, A.L.; Leroy, E. Lemniscates fitting to the contour of thermoplastic filaments pairs during viscous sintering. Mendeley Data 2020. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaunier, L.; Réguerre, A.-L.; Leroy, E. Contour Fitting of Fused Filaments Cross-Section Images by Lemniscates of Booth: Application to Viscous Sintering Kinetics Modeling. Polymers 2021, 13, 3965. https://doi.org/10.3390/polym13223965
Chaunier L, Réguerre A-L, Leroy E. Contour Fitting of Fused Filaments Cross-Section Images by Lemniscates of Booth: Application to Viscous Sintering Kinetics Modeling. Polymers. 2021; 13(22):3965. https://doi.org/10.3390/polym13223965
Chicago/Turabian StyleChaunier, Laurent, Anne-Laure Réguerre, and Eric Leroy. 2021. "Contour Fitting of Fused Filaments Cross-Section Images by Lemniscates of Booth: Application to Viscous Sintering Kinetics Modeling" Polymers 13, no. 22: 3965. https://doi.org/10.3390/polym13223965
APA StyleChaunier, L., Réguerre, A.-L., & Leroy, E. (2021). Contour Fitting of Fused Filaments Cross-Section Images by Lemniscates of Booth: Application to Viscous Sintering Kinetics Modeling. Polymers, 13(22), 3965. https://doi.org/10.3390/polym13223965