Nanocomposite of Fullerenes and Natural Rubbers: MARTINI Force Field Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Methodology
2.1. Molecular Dynamics Simulations
2.2. Calculation of Thermal and Mechanical Properties
2.3. Calculation of Solvation Free Energy
3. Results and Discussion
3.1. Coarse-Grained Model Based on MARTINI Force Field of cis-1,4-Polyisoprene
3.2. Effect of C60 Concentration on Macroscopic and Structural Properties of cis-PI Composites
3.3. Effect of C60 Concentration on Microscopic Properties of cis-PI Composites
3.3.1. Interaction of C60-C60 and C60-cis-PI
3.3.2. Diffusion of C60 and cis-PI in the Composites
3.4. Effect of C60 Concentration on C60 Solvation Free Energy
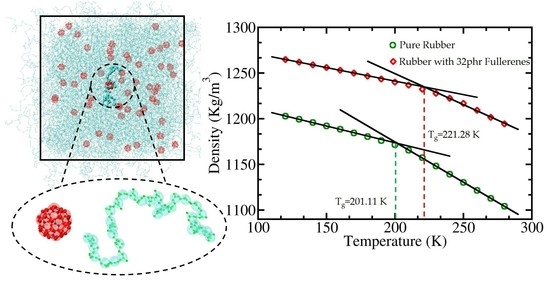
3.5. Effect of C60 Concentration on Glass Transition Temperature (Tg)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, C.Y. Cure characteristics and dynamic mechanical properties of acrylic rubber and epoxidized natural rubber blend. J. Ind. Eng. Chem. 2001, 7, 212–217. [Google Scholar]
- Chollakup, R.; Suethao, S.; Suwanruji, P.; Boonyarit, J.; Smitthipong, W. Mechanical properties and dissipation energy of carbon black/rubber composites. Compos. Adv. Mater. 2021, 30, 1–6. [Google Scholar] [CrossRef]
- Ray, S.S.; Okamoto, M. Polymer/layered silicate nanocomposites: A review from preparation to processing. Prog. Polym. Sci. 2003, 28, 1539–1641. [Google Scholar]
- Moniruzzaman, M.; Winey, K.I. Polymer nanocomposites containing carbon nanotubes. Macromolecules 2006, 39, 5194–5205. [Google Scholar] [CrossRef]
- Caseri, W. Nanocomposites of polymers and metals or semiconductors: Historical background and optical properties. Macromol. Rapid Commun. 2000, 21, 705–722. [Google Scholar] [CrossRef]
- Xie, X.-L.; Mai, Y.-W.; Zhou, X.-P. Dispersion and alignment of carbon nanotubes in polymer matrix: A review. Mater. Sci. Eng. R Rep. 2005, 49, 89–112. [Google Scholar] [CrossRef]
- Balazs, A.C.; Emrick, T.; Russell, T.P. Nanoparticle polymer composites: Where two small worlds meet. Science 2006, 314, 1107–1110. [Google Scholar] [CrossRef]
- Tee, B.C.K.; Wang, C.; Allen, R.; Bao, Z. An Electrically and Mechanically Self-Healing Composite with Pressure- and Flexion-Sensitive Properties for Electronic Skin Applications. Nat. Nanotechnol. 2012, 7, 825–832. [Google Scholar] [CrossRef] [PubMed]
- Du, F.; Scogna, R.C.; Zhou, W.; Brand, S.; Fischer, J.E.; Winey, K.I. Nanotube networks in polymer nanocomposites: Rheology and electrical conductivity. Macromolecules 2004, 37, 9048–9055. [Google Scholar] [CrossRef]
- Oh, H.; Green, P.F. Polymer chain dynamics and glass transition in athermal polymer/nanoparticle mixtures. Nat. Mater. 2009, 8, 139–143. [Google Scholar] [CrossRef] [PubMed]
- Rittigstein, P.; Priestley, R.D.; Broadbelt, L.J.; Torkelson, J.M. Model polymer nanocomposites provide an understanding of confinement effects in real nanocomposites. Nat. Mater. 2007, 6, 278–282. [Google Scholar] [CrossRef]
- Suethao, S.; Phongphanphanee, S.; Wong-Ekkabut, J.; Smitthipong, W. The Relationship between the Morphology and Elasticity of Natural Rubber Foam Based on the Concentration of the Chemical Blowing Agent. Polymers 2021, 13, 1091. [Google Scholar] [CrossRef]
- Suethao, S.; Ponloa, W.; Phongphanphanee, S.; Wong-Ekkabut, J.; Smitthipong, W. Current challenges in thermodynamic aspects of rubber foam. Sci. Rep. 2021, 11, 1–12. [Google Scholar]
- Wichaita, W.; Promlok, D.; Sudjaipraparat, N.; Sripraphot, S.; Suteewong, T.; Tangboriboonrat, P. A Concise Review on Design and Control of Structured Natural Rubber Latex Particles as Engineering Nanocomposites. Eur. Polym. J. 2021, 159, 110740. [Google Scholar] [CrossRef]
- Calabrese, M.A.; Chan, W.Y.; Av-Ron, S.H.; Olsen, B.D. Development of a Rubber Recycling Process Based on a Single-Component Interfacial Adhesive. ACS Appl. Polym. Mater. 2021, 3, 4849–4860. [Google Scholar] [CrossRef]
- Gielen, D.; Bennaceur, K.; Kerr, T.; Tam, C.; Tanaka, K.; Taylor, M.; Taylor, P. Tracking Industrial Energy Efficiency and CO2 Emissions; International Energy Agency: Paris, France, 2007. [Google Scholar]
- Phuhiangpa, N.; Ponloa, W.; Phongphanphanee, S.; Smitthipong, W. Performance of nano- and microcalcium carbonate in uncrosslinked natural rubber composites: New results of structure–properties relationship. Polymers 2020, 12, 2002. [Google Scholar] [CrossRef]
- Maiti, M.; Sadhu, S.; Bhowmick, A.K. Effect of carbon black on properties of rubber nanocomposites. J. Appl. Polym. Sci. 2005, 96, 443–451. [Google Scholar] [CrossRef]
- Araby, S.; Meng, Q.; Zhang, L.; Zaman, I.; Majewski, P.; Ma, J. Elastomeric composites based on carbon nanomaterials. Nanotechnology 2015, 26, 112001. [Google Scholar] [CrossRef] [PubMed]
- Sisanth, K.; Thomas, M.; Abraham, J.; Thomas, S. General introduction to rubber compounding. In Progress in Rubber Nanocomposites; Thomas, S., Maria, H.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1–39. [Google Scholar]
- Zhang, H.; Zhang, Z.; Zhao, G.; Liu, Y. Influence of carbon black with different concentration on dynamic properties and heat buildup of semi-efficient natural rubber composites. Micro Nano Lett. 2016, 11, 402–406. [Google Scholar] [CrossRef]
- Savetlana, S.; Zulhendri; Sukmana, I.; Saputra, F. The effect of carbon black loading and structure on tensile property of natural rubber composite. IOP Conf. Ser. Mater. Sci. Eng. 2017, 223, 012009. [Google Scholar] [CrossRef]
- Luheng, W.; Tianhuai, D.; Peng, W. Influence of carbon black concentration on piezoresistivity for carbon-black-filled silicone rubber composite. Carbon 2009, 47, 3151–3157. [Google Scholar] [CrossRef]
- Scagliusi, S.R.; Cardoso, E.C.L.; Parra, D.F.; Lima, L.F.C.P.; Lugão, A.B. Evaluation of “Payne effect” in radiation-induced modification of chlorobutyl rubber. Radiat. Phys. Chem. 2013, 84, 42–46. [Google Scholar] [CrossRef]
- Payne, A.R. The dynamic properties of carbon black-loaded natural rubber vulcanizates. Part I. J. Appl. Polym. Sci. 1962, 6, 57–63. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency. Compilation of Air Pollutant Emission Factors, 5th ed.; Office of Air Quality Planning and Standards: Durham, NC, USA, 1995. [Google Scholar]
- Yang, M.; Koutsos, V.; Zaiser, M. Interactions between polymers and carbon nanotubes: A molecular dynamics study. J. Phys. Chem. B 2005, 109, 10009–10014. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Eklund, P.C. Science of Fullerenes and Carbon Nanotubes: Their Properties and Applications; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- George, N.; Chandra, J.; Mathiazhagan, A.; Joseph, R. High performance natural rubber composites with conductive segregated network of multiwalled carbon nanotubes. Compos. Sci. Technol. 2015, 116, 33–40. [Google Scholar] [CrossRef]
- Chirvase, D.; Parisi, J.; Hummelen, J.C.; Dyakonov, V. Influence of nanomorphology on the photovoltaic action of polymer–fullerene composites. Nanotechnology 2004, 15, 1317–1323. [Google Scholar] [CrossRef] [Green Version]
- Thompson, B.C.; Fréchet, J.M.J. Polymer-fullerene composite solar cells. Angew. Chem. Int. Ed. 2008, 47, 58–77. [Google Scholar] [CrossRef]
- Dennler, G.; Scharber, M.C.; Brabec, C.J. Polymer-fullerene bulk-heterojunction solar cells. Adv. Mater. 2009, 21, 1323–1338. [Google Scholar] [CrossRef]
- Kausar, A. Fullerene nanofiller reinforced epoxy nanocomposites—Developments, progress and challenges. Mater. Res. Innov. 2020, 25, 175–185. [Google Scholar] [CrossRef]
- Al-Hartomy, O.A.; Al-Ghamdi, A.A.; Al-Salamy, F.; Dishovsky, N.; Slavcheva, D.; El-Tantawy, F. Properties of natural rubber-based composites containing fullerene. Int. J. Polym. Sci. 2012, 2012, 967276. [Google Scholar] [CrossRef] [Green Version]
- Jurkowska, B.; Jurkowski, B.; Kamrowski, P.; Pesetskii, S.S.; Koval, V.N.; Pinchuk, L.S.; Olkhov, Y.A. Properties of fullerene-containing natural rubber. J. Appl. Polym. Sci. 2006, 100, 390–398. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Cao, D.; Zhang, L.; Guo, Z. Nanoparticle dispersion and aggregation in polymer nanocomposites: Insights from molecular dynamics simulation. Langmuir 2011, 27, 7926–7933. [Google Scholar] [CrossRef]
- Guseva, D.V.; Komarov, P.V.; Lyulin, A.V. Molecular-dynamics simulations of thin polyisoprene films confined between amorphous silica substrates. J. Chem. Phys. 2014, 140, 114903. [Google Scholar] [CrossRef] [Green Version]
- Khuntawee, W.; Sutthibutpong, T.; Phongphanphanee, S.; Karttunen, M.; Wong-Ekkabut, J. Molecular dynamics study of natural rubber-fullerene composites: Connecting microscopic properties to macroscopic behavior. Phys. Chem. Chem. Phys. 2019, 21, 19403–19413. [Google Scholar] [CrossRef]
- Ghanbari, A.; Rahimi, M.; Dehghany, J. Influence of surface grafted polymers on the polymer dynamics in a silica-polystyrene nanocomposite: A coarse-grained molecular dynamics investigation. J. Phys. Chem. C 2013, 117, 25069–25076. [Google Scholar] [CrossRef]
- Davris, T.; Mermet-Guyennet, M.R.B.; Bonn, D.; Lyulin, A.V. Filler size effects on reinforcement in elastomer-based nanocomposites: Experimental and simulational insights into physical mechanisms. Macromolecules 2016, 49, 7077–7087. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Y.; Shen, J.; Gao, Y.; Zhang, L.; Cao, D. Polymer–nanoparticle interfacial behavior revisited: A molecular dynamics study. Phys. Chem. Chem. Phys. 2011, 13, 13058–13069. [Google Scholar] [CrossRef] [PubMed]
- Raffaini, G.; Citterio, A.; Galimberti, M.; Catauro, M. A Molecular dynamics study of noncovalent interactions between rubber and fullerenes. Macromol. Symp. 2021, 395, 2000198. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Forrest, B.M.; Suter, U.W. Accelerated equilibration of polymer melts by time-coarse-graining. J. Chem. Phys. 1995, 102, 7256–7266. [Google Scholar] [CrossRef]
- Akkermans, R.L.C.; Briels, W.J. A structure-based coarse-grained model for polymer melts. J. Chem. Phys. 2001, 114, 1020–1031. [Google Scholar] [CrossRef]
- Faller, R. Automatic coarse graining of polymers. Polymer 2004, 45, 3869–3876. [Google Scholar] [CrossRef] [Green Version]
- Reith, D.; Meyer, H.; Müller-Plathe, F. Mapping atomistic to coarse-grained polymer models using automatic simplex optimization to fit structural properties. Macromolecules 2001, 34, 2335–2345. [Google Scholar] [CrossRef] [Green Version]
- Nikunen, P.; Vattulainen, I.; Karttunen, M. Reptational dynamics in dissipative particle dynamics simulations of polymer melts. Phys. Rev. E 2007, 75, 036713. [Google Scholar] [CrossRef] [Green Version]
- Vettorel, T.; Besold, G.; Kremer, K. Fluctuating soft-sphere approach to coarse-graining of polymer models. Soft Matter 2010, 6, 2282–2292. [Google Scholar] [CrossRef]
- Huang, D.M.; Faller, R.; Do, K.; Moulé, A.J. Coarse-grained computer simulations of polymer/fullerene bulk heterojunctions for organic photovoltaic applications. J. Chem. Theory Comput. 2010, 6, 526–537. [Google Scholar] [CrossRef]
- Volgin, I.V.; Larin, S.V.; Lyulin, A.V.; Lyulin, S.V. Coarse-grained molecular-dynamics simulations of nanoparticle diffusion in polymer nanocomposites. Polymer 2018, 145, 80–87. [Google Scholar] [CrossRef] [Green Version]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [Green Version]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.J. The MARTINI coarse-grained force field: Extension to proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef]
- Marrink, S.J.; de Vries, A.H.; Mark, A.E. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar] [CrossRef] [Green Version]
- Wong-Ekkabut, J.; Baoukina, S.; Triampo, W.; Tang, I.-M.; Tieleman, D.P.; Monticelli, L. Computer simulation study of fullerene translocation through lipid membranes. Nat. Nanotechnol. 2008, 3, 363. [Google Scholar] [CrossRef]
- Rossi, G.; Monticelli, L.; Puisto, S.R.; Vattulainen, I.; Ala-Nissila, T. Coarse-graining polymers with the MARTINI force-field: Polystyrene as a benchmark case. Soft Matter 2011, 7, 698–708. [Google Scholar] [CrossRef] [Green Version]
- Uusitalo, J.J.; Ingólfsson, H.I.; Marrink, S.J.; Faustino, I. Martini coarse-grained force field: Extension to RNA. Biophys. J. 2017, 113, 246–256. [Google Scholar] [CrossRef] [Green Version]
- Nisoh, N.; Jarerattanachat, V.; Karttunen, M.; Wong-Ekkabut, J. Formation of aggregates, icosahedral structures and percolation clusters of fullerenes in lipids bilayers: The key role of lipid saturation. Biochim. Biophys. Acta Biomembr. 2020, 1862, 183328. [Google Scholar] [CrossRef]
- Nalakarn, P.; Boonnoy, P.; Nisoh, N.; Karttunen, M.; Wong-Ekkabut, J. Dependence of fullerene aggregation on lipid saturation due to a balance between entropy and enthalpy. Sci. Rep. 2019, 9, 1037. [Google Scholar] [CrossRef] [PubMed]
- Ingólfsson, H.I.; Melo, M.N.; van Eerden, F.J.; Arnarez, C.; Lopez, C.A.; Wassenaar, T.A.; Periole, X.; de Vries, A.H.; Tieleman, D.P.; Marrink, S.J. Lipid organization of the plasma membrane. J. Am. Chem. Soc. 2014, 136, 14554–14559. [Google Scholar] [CrossRef] [PubMed]
- Kitjanon, J.; Khuntawee, W.; Sutthibutpong, T.; Boonnoy, P.; Phongphanphanee, S.; Wong-ekkabut, J. Transferability of Polymer Chain Properties between Coarse-Grained and Atomistic Models of Natural Rubber Molecule Validated by Molecular Dynamics Simulations. J. Phys. Conf. Ser. 2017, 901, 012096. [Google Scholar] [CrossRef]
- Monticelli, L. On atomistic and coarse-grained models for C60 fullerene. J. Chem. Theory Comput. 2012, 8, 1370–1378. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Zykova-Timan, T.; Parrinello, M. Isothermal-isobaric molecular dynamics using stochastic velocity rescaling. J. Chem. Phys. 2009, 130, 074101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Ingólfsson, H.I.; Prieß, M.; Marrink, S.J.; Schäfer, L.V. Mixing MARTINI: Electrostatic coupling in hybrid atomistic-coarse-grained biomolecular simulations. J. Phys. Chem. B 2013, 117, 3516–3530. [Google Scholar] [CrossRef]
- Beu, T.A.; Ailenei, A.E.; Costinaş, R.I. Martini Force Field for Protonated Polyethyleneimine. J. Comput. Chem. 2020, 41, 349–361. [Google Scholar] [CrossRef] [PubMed]
- Wong-Ekkabut, J.; Karttunen, M. The good, the bad and the user in soft matter simulations. Biochim. Biophys. Acta Biomembr. 2016, 1858, 2529–2538. [Google Scholar] [CrossRef]
- Wong-Ekkabut, J.; Karttunen, M. Molecular dynamics simulation of water permeation through the alpha-hemolysin channel. J. Biol. Phys. 2016, 42, 133–146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boonnoy, P.; Karttunen, M.; Wong-Ekkabut, J. Does α-tocopherol flip-flop help to protect membranes against oxidation? J. Phys. Chem. B 2018, 122, 10362–10370. [Google Scholar] [CrossRef] [PubMed]
- Enkavi, G.; Javanainen, M.; Kulig, W.; Róg, T.; Vattulainen, I. Multiscale simulations of biological membranes: The challenge to understand biological phenomena in a living substance. Chem. Rev. 2019, 119, 5607–5774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Buchholz, J.; Paul, W.; Varnik, F.; Binder, K. Cooling rate dependence of the glass transition temperature of polymer melts: Molecular dynamics study. J. Chem. Phys. 2002, 117, 7364–7372. [Google Scholar] [CrossRef]
- Glova, A.D.; Falkovich, S.G.; Dmitrienko, D.I.; Lyulin, A.V.; Larin, S.V.; Nazarychev, V.M.; Karttunen, M.; Lyulin, S.V. Scale-dependent miscibility of polylactide and polyhydroxybutyrate: Molecular dynamics simulations. Macromolecules 2018, 51, 552–563. [Google Scholar] [CrossRef] [Green Version]
- Sharma, P.; Roy, S.; Karimi-Varzaneh, H.A. Validation of force fields of rubber through glass-transition temperature calculation by microsecond atomic-scale molecular dynamics simulation. J. Phys. Chem. B 2016, 120, 1367–1379. [Google Scholar] [CrossRef]
- Van Gunsteren, W.F.; Weiner, P.K.; Wilkinson, A.J. Computer Simulation of Biomolecular Systems: Theoretical and Experimental Applications; Springer Science & Business Media: Berlin, Germany, 2013; Volume 3. [Google Scholar]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Graessley, W.W. Chain dimensions and entanglement spacings in dense macromolecular systems. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1023–1033. [Google Scholar] [CrossRef]
- Tobolsky, A.V.; Mark, H.F. Polymer Science and Materials; John Wiley and Sons: Hoboken, NJ, USA, 1971. [Google Scholar]
- Brandrup, J.; Immergut, E.H.; Grulke, E.A.; Abe, A.; Bloch, D.R. Polymer Handbook; John Wiley and Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Holownia, B.P. Effect of carbon black on Poisson’s ratio of elastomers. Rubber Chem. Technol. 1975, 48, 246–253. [Google Scholar] [CrossRef]
- Guenza, M. Structural and thermodynamic consistency in coarse-grained models of macromolecules. J. Phys. Conf. Ser. 2015, 640, 012009. [Google Scholar] [CrossRef]
- Potestio, R.; Peter, C.; Kremer, K. Computer simulations of soft matter: Linking the scales. Entropy 2014, 16, 4199–4245. [Google Scholar] [CrossRef] [Green Version]
- Van der Wal, C.W.; Bree, H.W.; Schwarzl, F.R. Mechanical properties of highly filled elastomers. II. Relationship between filler characteristics, thermal expansion, and bulk moduli. J. Appl. Polym. Sci. 1965, 9, 2143–2166. [Google Scholar] [CrossRef]
- Wei, C.; Srivastava, D.; Cho, K. Thermal expansion and diffusion coefficients of carbon nanotube-polymer composites. Nano Lett. 2002, 2, 647–650. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Tambraparni, M.; Qiu, J.; Tipton, J.; Dean, D. Thermal expansion of graphene composites. Macromolecules 2009, 42, 5251–5255. [Google Scholar] [CrossRef]
- Vettorel, T.; Kremer, K. Development of entanglements in a fully disentangled polymer melt. Macromol. Theory Simul. 2010, 19, 44–56. [Google Scholar] [CrossRef]
- Mcquarrie, D. Statistical Mechanics; Harper & Row: New York, NY, USA, 1976. [Google Scholar]
- Trzesniak, D.; Kunz, A.P.E.; van Gunsteren, W.F. A comparison of methods to compute the potential of mean force. Chemphyschem 2007, 8, 162–169. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Peng, Y.; Li, S.; Liu, L.; Yan, T. Molecular dynamics simulation of fullerene C60 in ethanol solution. J. Phys. Chem. C 2009, 113, 3096–3104. [Google Scholar] [CrossRef]
- Al-Qattan, M.N.; Deb, P.K.; Tekade, R.K. Molecular dynamics simulation strategies for designing carbon-nanotube-based targeted drug delivery. Drug Discov. Today 2018, 23, 235–250. [Google Scholar] [CrossRef]
- Nisoh, N.; Karttunen, M.; Monticelli, L.; Wong-Ekkabut, J. Lipid monolayer disruption caused by aggregated carbon nanoparticles. RSC Adv. 2015, 5, 11676–11685. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Cagin, T. Coarse grain modeling of polyimide copolymers. Polymer 2010, 51, 2786–2794. [Google Scholar] [CrossRef]
- Sillescu, H. Heterogeneity at the glass transition: A review. J. Non -Cryst. Solids 1999, 243, 81–108. [Google Scholar] [CrossRef]






| Properties | Exp. | United Atom [38] | CG |
|---|---|---|---|
| Density; kg/m3 | 910 [80] | 853.9 ± 1.6 | 1087 ± 2.30 |
| Bulk modulus; GPa | 2.02 [83] | 1.37 ± 0.02 | 0.53 ± 0.00 |
| Thermal expansion; (10−4/K) | 6.1 [81,82] | 7.80 ± 0.15 | 9.25 ± 0.02 |
| < > | - | 12.85 ± 0.41 | 13.28 ± 0.06 |
| < > | - | 2.07 ± 0.04 | 2.17 ± 0.01 |
| - | 6.20 | 6.11 |
| C60 Concentration (phr) | < R0 > (nm) | < Rg > (nm) | |
|---|---|---|---|
| 0 | 3.64 ± 0.06 | 1.47 ± 0.01 | 6.11 |
| 4 | 3.65 ± 0.06 | 1.48 ± 0.01 | 6.11 |
| 8 | 3.66 ± 0.06 | 1.48 ± 0.01 | 6.12 |
| 16 | 3.67 ± 0.06 | 1.48 ± 0.01 | 6.12 |
| 32 | 3.71 ± 0.06 | 1.50 ± 0.01 | 6.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kitjanon, J.; Khuntawee, W.; Phongphanphanee, S.; Sutthibutpong, T.; Chattham, N.; Karttunen, M.; Wong-ekkabut, J. Nanocomposite of Fullerenes and Natural Rubbers: MARTINI Force Field Molecular Dynamics Simulations. Polymers 2021, 13, 4044. https://doi.org/10.3390/polym13224044
Kitjanon J, Khuntawee W, Phongphanphanee S, Sutthibutpong T, Chattham N, Karttunen M, Wong-ekkabut J. Nanocomposite of Fullerenes and Natural Rubbers: MARTINI Force Field Molecular Dynamics Simulations. Polymers. 2021; 13(22):4044. https://doi.org/10.3390/polym13224044
Chicago/Turabian StyleKitjanon, Jiramate, Wasinee Khuntawee, Saree Phongphanphanee, Thana Sutthibutpong, Nattaporn Chattham, Mikko Karttunen, and Jirasak Wong-ekkabut. 2021. "Nanocomposite of Fullerenes and Natural Rubbers: MARTINI Force Field Molecular Dynamics Simulations" Polymers 13, no. 22: 4044. https://doi.org/10.3390/polym13224044
APA StyleKitjanon, J., Khuntawee, W., Phongphanphanee, S., Sutthibutpong, T., Chattham, N., Karttunen, M., & Wong-ekkabut, J. (2021). Nanocomposite of Fullerenes and Natural Rubbers: MARTINI Force Field Molecular Dynamics Simulations. Polymers, 13(22), 4044. https://doi.org/10.3390/polym13224044