Deep Insight into the Influences of the Intrinsic Properties of Dielectric Elastomer on the Energy-Harvesting Performance of the Dielectric Elastomer Generator
Abstract
:1. Introduction
2. Modeling of DEG
2.1. Setup of Device Variables
2.2. The Description of Mechanical Loss Behavior
2.3. The Description of Electrical Loss Behavior
2.4. The Model of Energy Harvesting Performances of DEG
3. Results and Discussion
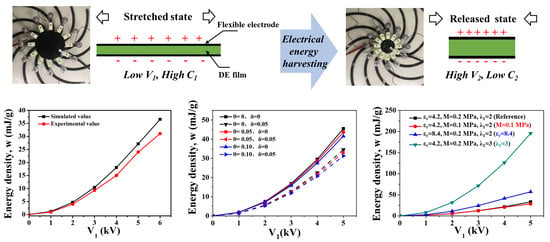
3.1. Experimental Validation
3.2. Influences of Intrinsic Properties of DE Materials on Energy-Harvesting Performance
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Osmani, B.; Seifi, S.; Park, H.S.; Leung, V.; Topper, T.; Muller, B. Nanomechanical probing of thin-film dielectric elastomer transducers. Appl. Phys. Lett. 2017, 111, 093104. [Google Scholar] [CrossRef] [Green Version]
- Brochu, P.; Pei, Q. Advances in dielectric elastomers for actuators and artificial muscles. Macromol. Rapid Commun. 2010, 31, 10–36. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Sun, H.; Liu, S.; Jiang, Y.; Yu, B.; Ning, N.; Tian, M.; Zhang, L. Mechanical, dielectric and actuated properties of carboxyl grafted silicone elastomer composites containing epoxy-functionalized TiO2 filler. Chem. Eng. J. 2020, 393, 124791. [Google Scholar] [CrossRef]
- Chu, B.; Zhou, X.; Ren, K.; Neese, B.; Lin, M.; Wang, Q.; Bauer, F.; Zhang, Q. A dielectric polymer with high electric energy density and fast discharge speed. Science 2006, 313, 334–336. [Google Scholar] [CrossRef] [PubMed]
- Pelrine, R.E.; Kornbluh, R.D.; Joseph, J.P. Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation. Sens. Actuators A Phys. 1998, 64, 77–85. [Google Scholar] [CrossRef]
- Carpi, F.; Anderson, I.; Bauer, S.; Frediani, G.; Gallone, G.; Gei, M.; Graaf, C.; Jean-Mistral, C.; Kaal, W.; Kofod, G.; et al. Standards for dielectric elastomer transducers. Smart Mater. Struct. 2015, 24, 105025. [Google Scholar] [CrossRef] [Green Version]
- Pelrine, R.; Kornbluh, R.; Eckerle, J.; Jeuck, P.; Oh, S.J.; Pei, Q.B.; Stanford, S. Dielectric elastomers: Generator mode fundamentals and applications. In Smart Structures and Materials 2001: Electroactive Polymer Actuators and Devices; BarCohen, Y., Ed.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2001; Volume 4329, pp. 148–156. [Google Scholar]
- Maas, J.; Graf, C. Dielectric elastomers for hydro power harvesting. Smart Mater. Struct. 2012, 21, 064006. [Google Scholar] [CrossRef]
- Kornbluh, R.D.; Pelrine, R.; Prahlad, H.; Wong-Foy, A.; McCoy, B.; Kim, S.; Eckerle, J.; Low, T. Dielectric elastomers: Stretching the capabilities of energy harvesting. MRS Bull. 2012, 37, 246–253. [Google Scholar] [CrossRef]
- Goudar, V.; Potkonjak, M. Dielectric Elastomer Generators for Foot Plantar Pressure Based Energy Scavenging. In Proceedings of the 11th IEEE Sensors Conference, Taipei, Taiwan, 28–31 October 2012; pp. 1001–1004. [Google Scholar]
- Bortot, E.; Gei, M. Harvesting energy with load-driven dielectric elastomer annular membranes deforming out-of-plane. Extrem. Mech. Lett. 2015, 5, 62–73. [Google Scholar] [CrossRef]
- Chen, S.E.; Deng, L.; He, Z.C.; Li, E.; Li, G.Y. Temperature effect on the performance of a dissipative dielectric elastomer generator with failure modes. Smart Mater. Struct. 2016, 25, 55017. [Google Scholar] [CrossRef]
- Zhang, C.L.; Lai, Z.H.; Rao, X.X.; Zhang, J.W.; Yurchenko, D. Energy harvesting from a novel contact-type dielectric elastomer generator. Energy Convers. Manag. 2020, 205, 112351. [Google Scholar] [CrossRef]
- Zhang, C.L.; Lai, Z.H.; Zhang, G.Q.; Yurchenko, D. Energy harvesting from a dynamic vibro-impact dielectric elastomer generator subjected to rotational excitations. Nonlinear Dyn. 2020, 102, 1271–1284. [Google Scholar] [CrossRef]
- Moretti, G.; Righi, M.; Vertechy, R.; Fontana, M. Fabrication and Test of an Inflated Circular Diaphragm Dielectric Elastomer Generator Based on PDMS Rubber Composite. Polymers 2017, 9, 283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, Y.; Liu, S.; Zhong, M.; Zhang, L.; Ning, N.; Tian, M. Optimizing energy harvesting performance of cone dielectric elastomer generator based on VHB elastomer. Nano Energy 2020, 71, 104606. [Google Scholar] [CrossRef]
- McKay, T.; O’Brien, B.; Calius, E.; Anderson, I. Self-priming dielectric elastomer generators. Smart Mater. Struct. 2010, 19, 055025. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Y.; Wang, L.; Zhao, J. Experimental investigation on energy conversion for dielectric electroactive polymer generator. J. Intell. Mater. Syst. Struct. 2012, 23, 885–895. [Google Scholar]
- Wang, H.; Wang, C.; Yuan, T. On the energy conversion and efficiency of a dielectric electroactive polymer generator. Appl. Phys. Lett. 2012, 101, 033904. [Google Scholar] [CrossRef]
- McKay, T.; O’Brien, B.; Calius, E.; Anderson, I. An integrated, self-priming dielectric elastomer generator. Appl. Phys. Lett. 2010, 97, 062911. [Google Scholar] [CrossRef] [Green Version]
- Moretti, G.; Rosset, S.; Vertechy, R.; Anderson, I.; Fontana, M. A Review of Dielectric Elastomer Generator Systems. Adv. Intell. Syst. 2020, 2, 2000125. [Google Scholar] [CrossRef]
- Shian, S.; Huang, J.; Zhu, S.; Clarke, D.R. Optimizing the electrical energy conversion cycle of dielectric elastomer generators. Adv. Mater. 2014, 26, 6617–6621. [Google Scholar] [CrossRef]
- Fan, P.; Chen, H. Optimizing the Energy Harvesting Cycle of a Dissipative Dielectric Elastomer Generator for Performance Improvement. Polymers 2018, 10, 1341. [Google Scholar] [CrossRef] [Green Version]
- Yin, G.; Yang, Y.; Song, F.; Renard, C.; Dang, Z.; Shi, C.; Wang, D. Dielectric elastomer generator with improved energy density and conversion efficiency based on polyurethane composites. ACS Appl. Mater. Interfaces 2017, 9, 5237–5243. [Google Scholar] [CrossRef]
- Pan, C.; Markvicka, E.J.; Malakooti, M.H.; Yan, J.; Hu, L.; Matyjaszewski, K.; Majidi, C. A Liquid-Metal-Elastomer Nanocomposite for Stretchable Dielectric Materials. Adv. Mater. 2019, 31, e1900663. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Xu, Y.; Ruan, M.; Xiao, Z.; Guo, W.; Wang, H.; Zhang, L. Improved electric energy density and conversion efficiency of natural rubber composites as dielectric elastomer generators. AIP Adv. 2019, 9, 025035. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Gao, Z.; Yang, M.; Zheng, M.; Wang, D.; Zha, J.; Wen, Y.; Dang, Z. Enhanced energy conversion efficiency in the surface modified BaTiO3 nanoparticles/polyurethane nanocomposites for potential dielectric elastomer generators. Nano Energy 2019, 59, 363–371. [Google Scholar] [CrossRef]
- Ellingford, C.; Zhang, R.; Wemyss, A.M.; Zhang, Y.; Brown, O.B.; Zhou, H.; Keogh, P.; Bowen, C.; Wan, C. Self-Healing Dielectric Elastomers for Damage-Tolerant Actuation and Energy Harvesting. ACS Appl. Mater. Interfaces 2020, 12, 7595–7604. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Song, F.L.; Lin, X.; Wang, D.R. High-dielectric-permittivity silicone rubbers incorporated with polydopamine-modified ceramics and their potential application as dielectric elastomer generator. Mater. Chem. Phys. 2020, 241, 7. [Google Scholar] [CrossRef]
- Koh, S.J.A.; Keplinger, C.; Li, T.; Bauer, S.; Suo, Z. Dielectric elastomer generators: How much energy can be converted? IEEE/ASME Trans. Mechatron. 2011, 16, 33–41. [Google Scholar] [CrossRef]
- Koh, S.J.A.; Zhao, X.; Suo, Z. Maximal energy that can be converted by a dielectric elastomer generator. Appl. Phys. Lett. 2009, 94, 262902. [Google Scholar] [CrossRef] [Green Version]
- Foo, C.C.; Koh, S.J.A.; Keplinger, C.; Kaltseis, R.; Bauer, S.; Suo, Z. Performance of dissipative dielectric elastomer generators. J. Appl. Phys. 2012, 111, 094107. [Google Scholar]
- Eilaghi, A.; Flanagan, J.G.; Tertinegg, I.; Simmons, C.A.; Brodland, G.W.; Ethier, C.R. Biaxial mechanical testing of human sclera. J. Biomech. 2010, 43, 1696–1701. [Google Scholar] [PubMed]
- Ehabe, E.; Bonfils, F.; Aymard, C.; Akinlabi, A.K.; Sainte Beuve, J. Modelling of Mooney viscosity relaxation in natural rubber. Polym. Test. 2005, 24, 620–627. [Google Scholar] [CrossRef]
- Oman, S.; Nagode, M. Observation of the relation between uniaxial creep and stress relaxation of filled rubber. Mater. Des. 2014, 60, 451–457. [Google Scholar]
- TuanDung, N.; Li, J.; Sun, L.; DanhQuang, T.; Xuan, F. Viscoelasticity Modeling of Dielectric Elastomers by Kelvin Voigt-Generalized Maxwell Model. Polymers 2021, 13, 2203. [Google Scholar]
- Carniel, E.L.; Fontanella, C.G.; Stefanini, C.; Natali, A.N. A procedure for the computational investigation of stress-relaxation phenomena. Mech. Time-Depend. Mater. 2013, 17, 25–38. [Google Scholar] [CrossRef]
- Kofod, G. The static actuation of dielectric elastomer actuators: How does pre-stretch improve actuation? J. Phys. D Appl. Phys. 2008, 41, 215405. [Google Scholar] [CrossRef]
- Vu-Cong, T.; Jean-Mistral, C.; Sylvestre, A. Impact of the nature of the compliant electrodes on the dielectric constant of acrylic and silicone electroactive polymers. Smart Mater. Struct. 2012, 21, 105036. [Google Scholar] [CrossRef]
- Cha, H.-S.; Yu, B.; Lee, Y.-K. Changes in stress relaxation property and softness of soft denture lining materials after cyclic loading. Dent. Mater. 2011, 27, 291–297. [Google Scholar] [CrossRef] [PubMed]









| DE Film Shape and Variables | Value |
|---|---|
| thickness, z0/mm | 0.5 |
| radius, r0/mm | 20 |
| bias voltage, V1/kV | 0, 1, 2, 3, 4, 5 |
| stress relaxation ratio, θ | 0, 0.05, 0.1 |
| charge leakage ratio, δ | 0, 0.05 |
| elastic coefficient, M/MPa | 0.2, 0.1 |
| permittivity, εr | 4.2, 8.4 |
| stretched state ratio, λ1 | 2, 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Li, Y.; Yang, H.; Ning, N.; Tian, M.; Zhang, L. Deep Insight into the Influences of the Intrinsic Properties of Dielectric Elastomer on the Energy-Harvesting Performance of the Dielectric Elastomer Generator. Polymers 2021, 13, 4202. https://doi.org/10.3390/polym13234202
Jiang Y, Li Y, Yang H, Ning N, Tian M, Zhang L. Deep Insight into the Influences of the Intrinsic Properties of Dielectric Elastomer on the Energy-Harvesting Performance of the Dielectric Elastomer Generator. Polymers. 2021; 13(23):4202. https://doi.org/10.3390/polym13234202
Chicago/Turabian StyleJiang, Yingjie, Yujia Li, Haibo Yang, Nanying Ning, Ming Tian, and Liqun Zhang. 2021. "Deep Insight into the Influences of the Intrinsic Properties of Dielectric Elastomer on the Energy-Harvesting Performance of the Dielectric Elastomer Generator" Polymers 13, no. 23: 4202. https://doi.org/10.3390/polym13234202
APA StyleJiang, Y., Li, Y., Yang, H., Ning, N., Tian, M., & Zhang, L. (2021). Deep Insight into the Influences of the Intrinsic Properties of Dielectric Elastomer on the Energy-Harvesting Performance of the Dielectric Elastomer Generator. Polymers, 13(23), 4202. https://doi.org/10.3390/polym13234202