Thermal Conductivities of Crosslinked Polyisoprene and Polybutadiene from Molecular Dynamics Simulations
Abstract
:1. Introduction
2. Simulation Details
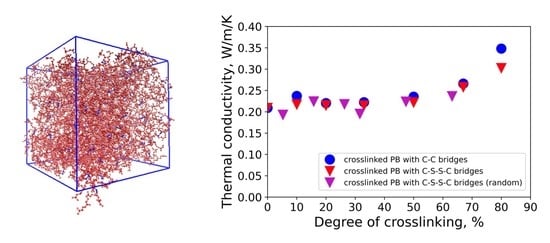
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rossinsky, E.; Müller-Plathe, F. Anisotropy of the thermal conductivity in a crystalline polymer: Reverse nonequilibrium molecular dynamics simulation of the δ phase of syndiotactic polystyrene. J. Chem. Phys. 2009, 130, 134905. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yang, R. Tuning the thermal conductivity of polymers with mechanical strains. Phys. Rev. B 2010, 81, 174122. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, J.W.; Wei, N.; Zhang, Y.; Rabczuk, T. Thermal conductivity dependence on chain length in amorphous polymers. J. Appl. Phys. 2013, 113, 184304. [Google Scholar] [CrossRef]
- He, Y.; Lian-Xiang, M.; Tang, Y.Z.; Wang, Z.P.; Li, W.; Kukulka, D. Thermal Conductivity of Natural Rubber Using Molecular Dynamics Simulation. J. Nanosci. Nanotechnol. 2015, 15, 3244–3248. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Yu, X.; Bao, H.; Yang, N. High Thermal Conductivity of Bulk Epoxy Resin by Bottom-Up Parallel-Linking and Strain: A Molecular Dynamics Study. J. Phys. Chem. C 2018, 122, 13140–13147. [Google Scholar] [CrossRef] [Green Version]
- Engelmann, S.; Meyer, J.; Hentschke, R. Computer simulation of thermal conductivity in vulcanized polyisoprene at variable strain and temperature. Phys. Rev. B 2017, 96, 054110. [Google Scholar] [CrossRef]
- Lussetti, E.; Terao, T.; Müller-Plathe, F. Nonequilibrium molecular dynamics calculation of the thermal conductivity of amorphous polyamide-6, 6. J. Phys. Chem. B 2007, 111, 11516–11523. [Google Scholar] [CrossRef] [PubMed]
- Algaer, E. Thermal Conductivity of Polymer Materials—Reverse Nonequilibrium Molecular Dynamics Simulations. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2010. [Google Scholar]
- Terao, T.; Lussetti, E.; Müller-Plathe, F. Nonequilibrium molecular dynamics methods for computing the thermal conductivity: Application to amorphous polymers. Phys. Rev. E 2007, 75, 057701. [Google Scholar] [CrossRef]
- Ueberreiter, K.; Otto-Laupenmühlen, E. Spezifische Wärme, spezifisches Volumen, Temperatur-und Wärmeleitfähigkeit von Hochpolymeren. Z. Naturforschung A 1953, 8, 664–673. [Google Scholar] [CrossRef]
- Hansen, D.; Kantayya, R.; Ho, C. Thermal conductivity of high polymers—the influence of molecular weight. Polym. Eng. Sci. 1966, 6, 260–262. [Google Scholar] [CrossRef]
- Hansen, D.; Ho, C.C. Thermal conductivity of high polymers. J. Polym. Sci. Part A Gen. Pap. 1965, 3, 659–670. [Google Scholar] [CrossRef]
- Anderson, D. Thermal conductivity of polymers. Chem. Rev. 1966, 66, 677–690. [Google Scholar] [CrossRef]
- Xiong, X.; Yang, M.; Liu, C.; Li, X.; Tang, D. Thermal conductivity of cross-linked polyethylene from molecular dynamics simulation. J. Appl. Phys. 2017, 122, 035104. [Google Scholar] [CrossRef]
- Kikugawa, G.; Desai, T.G.; Keblinski, P.; Ohara, T. Effect of crosslink formation on heat conduction in amorphous polymers. J. Appl. Phys. 2013, 114, 034302. [Google Scholar] [CrossRef] [Green Version]
- Monk, J.D.; Bucholz, E.W.; Boghozian, T.; Deshpande, S.; Schieber, J.; Bauschlicher, C.W., Jr.; Lawson, J.W. Computational and experimental study of phenolic resins: Thermal–mechanical properties and the role of hydrogen bonding. Macromolecules 2015, 48, 7670–7680. [Google Scholar] [CrossRef]
- Monk, J.D.; Haskins, J.B.; Bauschlicher, C.W., Jr.; Lawson, J.W. Molecular dynamics simulations of phenolic resin: Construction of atomistic models. Polymer 2015, 62, 39–49. [Google Scholar] [CrossRef]
- Yamamoto, O. Thermal conductivity of cross-linked polymers. Polym. J. 1971, 2, 509–517. [Google Scholar] [CrossRef] [Green Version]
- Huo, R.; Zhang, Z.; Athir, N.; Fan, Y.; Liu, J.; Shi, L. Designing high thermal conductivity of cross-linked epoxy resin via Molecular Dynamics Simulation. Phys. Chem. Chem. Phys. 2020, 22, 19735–19745. [Google Scholar] [CrossRef]
- Rashidi, V.; Coyle, E.J.; Sebeck, K.; Kieffer, J.; Pipe, K.P. Thermal conductance in cross-linked polymers: Effects of non-bonding interactions. J. Phys. Chem. B 2017, 121, 4600–4609. [Google Scholar] [CrossRef]
- Toxvaerd, S.; Dyre, J.C. Communication: Shifted forces in molecular dynamics. J. Chem. Phys. 2011, 134, 081102. [Google Scholar] [CrossRef] [Green Version]
- Harmandaris, V.; Doxastakis, M.; Mavrantzas, V.; Theodorou, D. Detailed molecular dynamics simulation of the self-diffusion of n-alkane and cis-1, 4 polyisoprene oligomer melts. J. Chem. Phys. 2002, 116, 436–446. [Google Scholar] [CrossRef] [Green Version]
- Carwile, L.C.; Hoge, H.J. Thermal Conductivity of Soft Vulcanized Natural Rubber: Selected Values. R. Chem. Tech. 1966, 39, 126–131. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Vasilev, A.; Lorenz, T.; Breitkopf, C. Thermal Conductivity of Polyisoprene and Polybutadiene from Molecular Dynamics Simulations and Transient Measurements. Polymers 2020, 12, 1081. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W. OPLS All-Atom Parameters for Organic Molecules, Ions, Peptides & Nucleic Acids; Yale University: New Haven, CT, USA, 2009. [Google Scholar]
- Jewett, A.I.; Zhuang, Z.; Shea, J.E. Moltemplate a coarse-grained model assembly tool. Biophys. J. 2013, 104, 169a. [Google Scholar] [CrossRef] [Green Version]
- Kruželák, J.; Sỳkora, R.; Hudec, I. Vulcanization of rubber compounds with peroxide curing systems. Rubber Chem. Technol. 2017, 90, 60–88. [Google Scholar] [CrossRef]
- Kvasničáková, A.; Kruželák, J.; Medlenová, E.; Dosoudil, R.; Hudec, I.; Gořalík, M. Rubber magnets cured with peroxide and coagents. J. Elastomers Plast. 2020, 52, 253–270. [Google Scholar] [CrossRef]
- Kruželák, J.; Sỳkora, R.; Dosoudil, R.; Hudec, I. Relationship between the cross-link structure and properties of peroxide and sulfur-cured magnetic composites based on NR and NBR. J. Elastomers Plast. 2017, 49, 459–480. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Hager, J.; Hentschke, R.; Hojdis, N.W.; Karimi-Varzaneh, H.A. Computer simulation of particle–particle interaction in a model polymer nanocomposite. Macromolecules 2015, 48, 9039–9049. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Compute Heat/Flux Command. Available online: https://lammps.sandia.gov/doc/compute_heat_flux.html (accessed on 18 January 2021).
- Compute Centroid/Stress/Atom Command. Available online: https://lammps.sandia.gov/doc/compute_stress_atom.html (accessed on 18 January 2021).
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 2002, 65, 144306. [Google Scholar] [CrossRef] [Green Version]
- Nallasamy, P.; Mohan, S. Vibrational spectra of cis-1, 4-polyisoprene. Arab. J. Sci. Eng. 2004, 29, 17–26. [Google Scholar]
- Nallasamy, P.; Anbarasan, P.; Mohan, S. Vibrational spectra and assignments of cis- and trans-1,4-polybutadiene. Turk. J. Chem. 2002, 26, 105–112. [Google Scholar]
- Tsyurupa, M.; Davankov, V. Porous structure of hypercrosslinked polystyrene: State-of-the-art mini-review. React. Funct. Polym. 2006, 66, 768–779. [Google Scholar] [CrossRef]
- Tsyurupa, M.; Davankov, V. Hypercrosslinked polymers: Basic principle of preparing the new class of polymeric materials. React. Funct. Polym. 2002, 53, 193–203. [Google Scholar] [CrossRef]
- Pavlova, L.; Pavlov, M.; Davankov, V. The First Representatives of Hypercrosslinked Hydrophilic Networks: Alkylation and Polymerization of 4-Vinylpyridine in an Ionic Liquid. In Doklady Chemistry; Springer: Berlin/Heidelberg, Germany, 2006; Volume 406, pp. 6–8. [Google Scholar]
- Germain, J.; Fréchet, J.M.; Svec, F. Hypercrosslinked polyanilines with nanoporous structure and high surface area: Potential adsorbents for hydrogen storage. J. Mater. Chem. 2007, 17, 4989–4997. [Google Scholar] [CrossRef]
- Gent, A.N.; Sueyasu, T.; Wang, C. Tables of physical constants. In Engineering with Rubber; Elsevier: Amsterdam, The Netherlands, 2012; pp. 423–433. [Google Scholar]
- Wood, L. Polymer Handbook; Brandrup, J., Immergut, E.H., Eds.; Wiley: New York, NY, USA, 1975; Volume 7. [Google Scholar]
- Tonpheng, B.; Andersson, O. Crosslinking, thermal properties and relaxation behaviour of polyisoprene under high-pressure. Eur. Polym. J. 2008, 44, 2865–2873. [Google Scholar] [CrossRef]
- Tonpheng, B.; Yu, J.; Andersson, O. Effects of cross-links, pressure and temperature on the thermal properties and glass transition behaviour of polybutadiene. Phys. Chem. Chem. Phys. 2011, 13, 15047–15054. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilev, A.; Lorenz, T.; Breitkopf, C. Thermal Conductivities of Crosslinked Polyisoprene and Polybutadiene from Molecular Dynamics Simulations. Polymers 2021, 13, 315. https://doi.org/10.3390/polym13030315
Vasilev A, Lorenz T, Breitkopf C. Thermal Conductivities of Crosslinked Polyisoprene and Polybutadiene from Molecular Dynamics Simulations. Polymers. 2021; 13(3):315. https://doi.org/10.3390/polym13030315
Chicago/Turabian StyleVasilev, Aleksandr, Tommy Lorenz, and Cornelia Breitkopf. 2021. "Thermal Conductivities of Crosslinked Polyisoprene and Polybutadiene from Molecular Dynamics Simulations" Polymers 13, no. 3: 315. https://doi.org/10.3390/polym13030315
APA StyleVasilev, A., Lorenz, T., & Breitkopf, C. (2021). Thermal Conductivities of Crosslinked Polyisoprene and Polybutadiene from Molecular Dynamics Simulations. Polymers, 13(3), 315. https://doi.org/10.3390/polym13030315