Interface Strength and Fiber Content Influence on Corn Stover Fibers Reinforced Bio-Polyethylene Composites Stiffness
Abstract
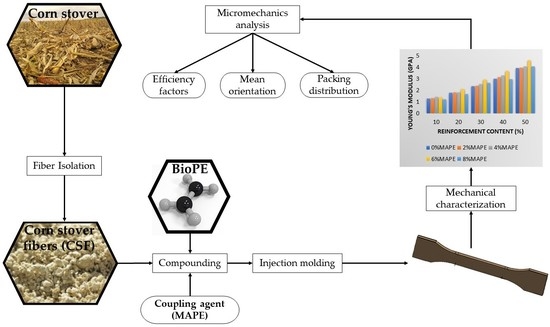
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Fiber Isolation from Corn Stover Waste
2.2.2. Composite Compounding
2.2.3. Composite Injection Molding and Characterization
3. Results
3.1. Impact of the Coupling Agent Content Over the Young’s Modulus
3.2. Impact of the Reinforcement Content Over the Young’s Modulus of the Composites
3.3. Contribution of the Fibers to the Young’s Modulus of the Composites
3.4. Micromechanics of the Young’s Moduli of the Composites
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomason, J.; Jenkins, P.; Yang, L. Glass Fibre Strength—A Review with Relation to Composite Recycling. Fibers 2016, 4, 18. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Lauke, B.; Mäder, E.; Yue, C.-Y.; Hu, X. Tensile properties of short-glass-fiber-and short-carbon-fiber-reinforced polypropylene composites. Compos. Part A Appl. Sci. Manuf. 2000, 31, 1117–1125. [Google Scholar] [CrossRef]
- Akonda, M.H.; Lawrence, C.A.; Weager, B.M. Recycled carbon fibre-reinforced polypropylene thermoplastic composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 79–86. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, S.; Xu, G.; Zhu, X.; Liu, W. Mechanical, Flammability, and Crystallization Behavior of Polypropylene Composites Reinforced by Aramid Fibers. J. Appl. Polym. Sci. 2012, 125, 1166–1175. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L.; Cui, X.; Guo, W. Crystallization behavior and properties of glass fiber reinforced polypropylene composites. Polymers 2019, 11, 1198. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.S.; Bhatnagar, N.; Ghosh, A.K. Development of long glass fiber reinforced polypropylene composites: Mechanical and morphological characteristics. J. Reinf. Plast. Compos. 2007, 26, 239–249. [Google Scholar] [CrossRef]
- Malkapuram, R.; Kumar, V.; Singh Negi, Y. Recent development in natural fiber reinforced polypropylene composites. J. Reinf. Plast. Compos. 2009, 28, 1169–1189. [Google Scholar] [CrossRef]
- Domínguez-Robles, J.; Stewart, S.A.; Rendl, A.; González, Z.; Donnelly, R.F.; Larrañeta, E. Lignin and cellulose blends as pharmaceutical excipient for tablet manufacturing via direct compression. Biomolecules 2019, 9, 423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, J.M.; Quang, S.T.; Hwang, B.S.; DeVries, K.L. Interfacial evaluation of modified Jute and Hemp fibers/polypropylene (PP)-maleic anhydride polypropylene copolymers (PP-MAPP) composites using micromechanical technique and nondestructive acoustic emission. Compos. Sci. Technol. 2006, 66, 2686–2699. [Google Scholar] [CrossRef]
- Nygård, P.; Tanem, B.S.; Karlsen, T.; Brachet, P.; Leinsvang, B. Extrusion-based wood fibre-PP composites: Wood powder and pelletized wood fibres—A comparative study. Compos. Sci. Technol. 2008, 68, 3418–3424. [Google Scholar] [CrossRef]
- Tarrés, Q.; Vilaseca, F.; Herrera-Franco, P.J.; Espinach, F.X.; Delgado-Aguilar, M.; Mutjé, P. Interface and micromechanical characterization of tensile strength of bio-based composites from polypropylene and henequen strands. Ind. Crop. Prod. 2019, 132, 319–326. [Google Scholar] [CrossRef]
- Wambua, P.; Ivens, J.; Verpoest, I. Natural fibres: Can they replace glass in fibre reinforced plastics? Compos. Sci. Technol. 2003, 63, 1259–1264. [Google Scholar] [CrossRef]
- Koronis, G.; Silva, A.; Fontul, M. Green composites: A review of adequate materials for automotive applications. Compos. Part B Eng. 2013, 44, 120–127. [Google Scholar] [CrossRef]
- Sullins, T.; Pillay, S.; Komus, A.; Ning, H. Hemp fi ber reinforced polypropylene composites: The effects of material treatments. Compos. Part B 2017, 114, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Pendrill, F.; Persson, U.M.; Godar, J.; Kastner, T.; Moran, D.; Schmidt, S.; Wood, R. Agricultural and forestry trade drives large share of tropical deforestation emissions. Glob. Environ. Chang. 2019, 56, 1–10. [Google Scholar] [CrossRef]
- Maraveas, C. Production of sustainable and biodegradable polymers from agricultural waste. Polymers 2020, 12, 1127. [Google Scholar] [CrossRef]
- Gontard, N.; Sonesson, U.; Birkved, M.; Majone, M.; Bolzonella, D.; Celli, A.; Angellier-Coussy, H.; Jang, G.W.; Verniquet, A.; Broeze, J.; et al. A research challenge vision regarding management of agricultural waste in a circular bio-based economy. Crit. Rev. Environ. Sci. Technol. 2018, 48, 614–654. [Google Scholar] [CrossRef] [Green Version]
- Al-Oqla, F.M.; Salit, M.S.; Ishak, M.R.; Aziz, N.A. Combined multi-criteria evaluation stage technique as an agro waste evaluation indicator for polymeric composites: Date palm fibers as a case study. BioResources 2014, 9, 4608–4621. [Google Scholar] [CrossRef] [Green Version]
- Tarrés, Q.; Espinosa, E.; Domínguez-Robles, J.; Rodríguez, A.; Mutjé, P.; Delgado-Aguilar, M. The suitability of banana leaf residue as raw material for the production of high lignin content micro/nano fibers: From residue to value-added products. Ind. Crop. Prod. 2017, 99, 27–33. [Google Scholar]
- Vargas, F.; Gonzalez, Z.; Sanchez, R.; Jimenez, L.; Rodriguez, A. Cellulosic pulps of cereal straws as raw material for the manufacture of ecological packaging. BioResources 2012, 7, 4161–4170. [Google Scholar]
- Delgado-Aguilar, M.; Vilaseca, F.; Tarrés, Q.; Julián, F.; Mutjé, P.; Espinach, F.X. Extending the value chain of corn agriculture by evaluating technical feasibility and the quality of the interphase of chemo-thermomechanical fiber from corn stover reinforced polypropylene biocomposites. Compos. Part B Eng. 2018, 137, 16–22. [Google Scholar] [CrossRef]
- Millard, E. Incorporating agroforestry approaches into commodity value chains. Environ. Manag. 2011, 48, 365–377. [Google Scholar] [CrossRef]
- Espinosa, E.; Domínguez-Robles, J.; Sánchez, R.; Tarrés, Q.; Rodríguez, A. The effect of pre-treatment on the production of lignocellulosic nanofibers and their application as a reinforcing agent in paper. Cellulose 2017, 24, 2605–2618. [Google Scholar] [CrossRef]
- Domínguez-Robles, J.; Tarrés, Q.; Delgado-Aguilar, M.; Rodríguez, A.; Espinach, F.X.; Mutjé, P. Approaching a new generation of fiberboards taking advantage of self lignin as green adhesive. Int. J. Biol. Macromol. 2018, 108, 927–935. [Google Scholar] [CrossRef] [PubMed]
- Borrero-lópez, A.M.; Valencia, C.; Blánquez, A.; Hernández, M.; Eugenio, M.E.; Franco, J.M. Cellulose pulp- and castor oil-based polyurethanes for lubricating applications: Influence of streptomyces action on barley and wheat straws. Polymers 2020, 12, 2822. [Google Scholar] [CrossRef] [PubMed]
- Aguado, R.; Moral, A.; Mutje, P.; Tijero, A. Rapeseed stalks for papermaking: Studies on pulping, refining and dewatering. Cellul. Chem. Technol. 2015, 49, 833–839. [Google Scholar]
- Hubbe, M.A.; Venditti, R.A.; Rojas, O.J. What happens to cellulosic fibers during papermaking and recycling? A review. BioResources 2007, 2, 739–788. [Google Scholar]
- Moral, A.; Aguado, R.; Tijero, A.; Tarrés, Q.; Delgado-Aguilar, M.; Mutjé, P. High-yield pulp from Brassica napus to manufacture packaging paper. BioResources 2017, 12, 2792–2804. [Google Scholar] [CrossRef] [Green Version]
- Anastas, P.; Zimmerman, J.B. Through the 12 Principles of Green Engineering. Environ. Sci. Technol. 2003, 37, 95A–101A. [Google Scholar] [CrossRef] [Green Version]
- Espinach, F.X.; Espinosa, E.; Reixach, R.; Rodríguez, A.; Mutjé, P.; Tarrés, Q. Study on the macro and micromechanics tensile strength properties of orange tree pruning fiber as sustainable reinforcement on bio-polyethylene compared to oil-derived polymers and its composites. Polymers 2020, 12, 2206. [Google Scholar] [CrossRef]
- Zheng, C.; Li, D.; Ek, M. Improving fire retardancy of cellulosic thermal insulating materials by coating with bio-based fire retardants. Nord. Pulp Pap. Res. J. 2019, 34, 96–106. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.T.H.; Qi, P.; Rostango, M.; Feteha, A.; Miller, S.A. The quest for high glass transition temperature bioplastics. J. Mater. Chem. A 2018, 6, 9298–9331. [Google Scholar] [CrossRef]
- Brodin, M.; Vallejos, M.; Opedal, M.T.; Area, M.C.; Chinga-Carrasco, G. Lignocellulosics as sustainable resources for production of bioplastics—A review. J. Clean. Prod. 2017, 162, 646–664. [Google Scholar] [CrossRef]
- Beckermann, G.W.; Pickering, K.L. Engineering and evaluation of hemp fibre reinforced polypropylene composites: Micro-mechanics and strength prediction modelling. Compos. Part A Appl. Sci. Manuf. 2009, 40, 210–217. [Google Scholar] [CrossRef]
- Vilaseca, F.; Valadez-Gonzalez, A.; Herrera-Franco, P.J.; Pelach, M.; Lopez, J.P.; Mutje, P. Biocomposites from abaca strands and polypropylene. Part I: Evaluation of the tensile properties. Bioresour. Technol. 2010, 101, 387–395. [Google Scholar] [CrossRef]
- Mohanty, S.; Verma, S.K.; Nayak, S.K. Dynamic mechanical and thermal properties of MAPE treated jute/HDPE composites. Compos. Sci. Technol. 2006, 66, 538–547. [Google Scholar] [CrossRef]
- Robertson, N.L.M.; Nychka, J.A.; Alemaskin, K.; Wolodko, J.D. Mechanical performance and moisture absorption of various natural fiber reinforced thermoplastic composites. J. Appl. Polym. Sci. 2013, 130, 969–980. [Google Scholar] [CrossRef]
- Tavares, T.D.; Antunes, J.C.; Ferreira, F.; Felgueiras, H.P. Biofunctionalization of natural fiber-reinforced biocomposites for biomedical applications. Biomolecules 2020, 10, 148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radoor, S.; Karayil, J.; Rangappa, S.M.; Siengchin, S.; Parameswaranpillai, J. A review on the extraction of pineapple, sisal and abaca fibers and their use as reinforcement in polymer matrix. Express Polym. Lett. 2020, 14, 309–335. [Google Scholar] [CrossRef]
- Manaia, J.P.; Manaia, A.T.; Rodriges, L. Industrial hemp fibers: An overview. Fibers 2019, 7, 106. [Google Scholar] [CrossRef] [Green Version]
- Neagu, R.C.; Gamstedt, E.K.; Berthold, F. Stiffness Contribution of Various Wood Fibers to Composite Materials. J. Compos. Mater. 2006, 40, 663–699. [Google Scholar] [CrossRef]
- López, J.P.; Mutjé, P.; Pèach, M.A.; El Mansouri, N.E.; Boufi, S.; Vilaseca, F. Analysis of the tensile modulus of polypropylene composites reinforced with stone groundwood fibers. BioResources 2012, 7, 1310–1323. [Google Scholar] [CrossRef]
- Kakou, C.A.; Arrakhiz, F.Z.; Trokourey, A.; Bouhfid, R.; Qaiss, A.; Rodrigue, D. Influence of coupling agent content on the properties of high density polyethylene composites reinforced with oil palm fibers. Mater. Des. 2014, 63, 641–649. [Google Scholar] [CrossRef]
- Vallejos, M.E.; Espinach, F.X.; Julián, F.; Torres, L.; Vilaseca, F.; Mutjé, P. Micromechanics of hemp strands in polypropylene composites. Compos. Sci. Technol. 2012, 72, 1209–1213. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre properties on the properties of glass-fibre-reinforced polyamide 6,6. J. Compos. Mater. 2000, 34, 158–172. [Google Scholar] [CrossRef]
- Hirsch, T.J. Modulus of Elasticity of Concrete Affected by Elastic Moduli of Cement Paste Matrix and Aggregate. J. Proc. 1962, 59, 427–452. [Google Scholar]
- Halpin, J.C. Effects of Environmental Factors on Composite Materials; Springer: Berlin/Heidelberg, Germany, 1969. [Google Scholar]
- Halpin, J.C.; Pagano, N.J. The Laminate Approximation for Randomly Oriented Fibrous Composites. J. Compos. Mater. 1969, 3, 720–724. [Google Scholar] [CrossRef]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29. [Google Scholar] [CrossRef]
- Espinach, F.X.; Julian, F.; Verdaguer, N.; Torres, L.; Pelach, M.A.; Vilaseca, F.; Mutje, P. Analysis of tensile and flexural modulus in hemp strands/polypropylene composites. Compos. Part B Eng. 2013, 47, 339–343. [Google Scholar] [CrossRef]
- Shah Mohammadi, M.; Ahmed, I.; Muja, N.; Rudd, C.D.; Bureau, M.N.; Nazhat, S.N. Effect of phosphate-based glass fibre surface properties on thermally produced poly(lactic acid) matrix composites. J. Mater. Sci. Mater. Med. 2011, 22, 2659–2672. [Google Scholar] [CrossRef]
- Peña, L.; González, I.; Bayer, R.J.; Mansouri, N.E.E.; Vilaseca, F. Mechanical behavior of thermo-mechanical corn stalk fibers in high density polyethylene composites. J. Biobased Mater. Bioenergy 2012, 6, 463–469. [Google Scholar] [CrossRef]
- Colom, X.; Carrasco, F.; Pagès, P.; Canavate, J. Effects of different treatments on the interface of HDPE/lignocellulosic fiber composites. Compos. Sci. Technol. 2003, 63, 161–169. [Google Scholar] [CrossRef]
- Tarrés, Q.; Ardanuy, M. Evolution of Interfacial Shear Strength and Mean Intrinsic Single Strength in Biobased Composites from Bio-Polyethylene and Thermo-Mechanical Pulp-Corn Stover Fibers. Polymers 2020, 12, 1308. [Google Scholar] [CrossRef] [PubMed]
- Shah, D.U.; Schubel, P.J.; Licence, P.; Clifford, M.J. Determining the minimum, critical and maximum fibre content for twisted yarn reinforced plant fibre composites. Compos. Sci. Technol. 2012, 72, 1909–1917. [Google Scholar] [CrossRef] [Green Version]
- Serrano, A.; Espinach, F.X.; Tresserras, J.; del Rey, R.; Pellicer, N.; Mutje, P. Macro and micromechanics analysis of short fiber composites stiffness: The case of old newspaper fibers–polypropylene composites. Mater. Des. 2014, 55, 319–324. [Google Scholar] [CrossRef] [Green Version]
- Reixach, R.; Espinach, F.X.; Franco-Marquès, E.; Ramirez de Cartagena, F.; Pellicer, N.; Tresserras, J.; Mutjé, P. Modeling of the Tensile Moduli of Mechanical, Thermomechanical, and Chemi-Thermomechanical Pulps from Orange Tree Pruning. Polym. Compos. 2013, 34, 1840–1846. [Google Scholar] [CrossRef]
- Granda, L.A.; Espinach, F.X.; López, F.; García, J.C.; Delgado-Aguilar, M.; Mutjé, P. Semichemical fibres of Leucaena collinsii reinforced polypropylene: Macromechanical and micromechanical analysis. Compos. Part B Eng. 2016, 91, 384–391. [Google Scholar] [CrossRef]
- Srinivas, K.; Lakshumu Naidu, A.; Raju Bahubalendruni, M.V.A. A review on chemical and mechanical properties of natural fiber reinforced polymer composites. Int. J. Performabil. Eng. 2017, 13, 189–200. [Google Scholar] [CrossRef] [Green Version]
- Krenchel, H. Fibre Reinforcement; Theoretical and Practical Investigations of the Elasticity and Strength of Fibre-Reinforced Materials; Akademisk Forlag: Oslo, Norway, 1964. [Google Scholar]
- Granda, L.A.; Espinach, F.X.; Mendez, J.A.; Tresserras, J.; Delgado-Aguilar, M.; Mutje, P. Semichemical fi bres of Leucaena collinsii reinforced polypropylene composites: Young â€TM s modulus analysis and fi bre diameter effect on the stiffness. Compos. Part B 2016, 92, 332–337. [Google Scholar] [CrossRef]
- Serra, A.; Tarr, Q.; Chamorro, M.-À.; Soler, J.; Mutj, P. Modeling the Stiffness of Coupled and Uncoupled Recycled Cotton Fibers Reinforced. Polymers 2019, 11, 1725. [Google Scholar] [CrossRef] [Green Version]
- Fukuda, H.; Kawata, K. On Young’s modulus of short fibre composites. Fibre Sci. Technol. 1974, 7, 207–222. [Google Scholar] [CrossRef]
- Sanomura, Y.; Kawamura, M. Fiber Orientation Control of Short-Fiber Reinforced Thermoplastics by Ram Extrusion. Polym. Compos. 2003, 24, 587–596. [Google Scholar] [CrossRef]



| Fiber Content (wt%) | MAPE Content (%) | ||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1.06 ± 0.03 | 10.59 ± 0.21 | 0.955 |
| 10 | 0 | 0.068 | 1.30 ± 0.02b | 6.37 ± 0.23 | 0.989 |
| 2 | 1.33 ± 0.03b | 6.75 ± 0.06 | |||
| 4 | 1.43 ± 0.02c | 6.73 ± 0.14 | |||
| 6 | 1.40 ± 0.02c | 6.44 ± 0.16 | |||
| 8 | 1.22 ± 0.02a | 6.45 ± 0.23 | |||
| 20 | 0 | 0.141 | 1.78 ± 0.02f | 4.65 ± 0.12 | 1.026 |
| 2 | 1.81 ± 0.02f | 4.89 ± 0.04 | |||
| 4 | 1.82 ± 0.04f | 5.96 ± 0.19 | |||
| 6 | 2.10 ± 0.03g | 5.66 ± 0.12 | |||
| 8 | 1.70 ± 0.02h | 5.91 ± 0.12 | |||
| 30 | 0 | 0.219 | 2.36 ± 0.03y | 2.58 ± 0.82 | 1.066 |
| 2 | 2.39 ± 0.03y | 3.02 ± 0.13 | |||
| 4 | 2.53 ± 0.02j | 4.65 ± 0.13 | |||
| 6 | 2.92 ± 0.04k | 4.90 ± 0.07 | |||
| 8 | 2.63 ± 0.03l | 5.13 ± 0.82 | |||
| 40 | 0 | 0.304 | 3.02 ± 0.03m | 1.72 ± 0.03 | 1.108 |
| 2 | 3.13 ± 0.02n | 2.79 ± 0.22 | |||
| 4 | 3.27 ± 0.04o | 4.45 ± 0.28 | |||
| 6 | 3.68 ± 0.03p | 4.15 ± 0.08 | |||
| 8 | 2.98 ± 0.03m | 4.22 ± 0.03 | |||
| 50 | 0 | 0.395 | 3.93 ± 0.03q | 1.98 ± 0.05 | 1.155 |
| 2 | 3.97 ± 0.02q | 1.97 ± 0.35 | |||
| 4 | 4.09 ± 0.03r | 3.66 ± 0.28 | |||
| 6 | 4.61 ± 0.04s | 3.24 ± 0.21 | |||
| 8 | 4.07 ± 0.02r | 3.34 ± 0.05 |
| MAPE (%) | (GPa) | (GPa) | MAPE (%) | (GPa) | (GPa) | |
|---|---|---|---|---|---|---|
| 0.068 | 0 | 8.4 | 7.2 | 6 | 13.2 | 12.5 |
| 0.141 | 12.2 | 11.1 | 17.8 | 18.3 | ||
| 0.219 | 14.1 | 13.1 | 20.4 | 21.6 | ||
| 0.304 | 15.1 | 14.1 | 20.5 | 21.1 |
| MAPE (%) | ||||
|---|---|---|---|---|
| 0.068 | 6 | 0.496 | 0.925 | 0.536 |
| 0.141 | 0.474 | 0.924 | 0.514 | |
| 0.219 | 0.468 | 0.922 | 0.508 | |
| 0.304 | 0.473 | 0.929 | 0.508 | |
| 0.395 | 0.476 | 0.931 | 0.511 |
| Rectangular | Triangular | Sinusoidal | ||||
|---|---|---|---|---|---|---|
| α | α | α | ||||
| 0.536 | 55.5 | 29.1 | 78.3 | 40.8 | 70.8 | 37.7 |
| 0.514 | 54.4 | 30.0 | 81.4 | 42.0 | 73.5 | 38.9 |
| 0.508 | 54.9 | 30.3 | 82.3 | 42.4 | 74.3 | 39.2 |
| 0.508 | 54.9 | 30.3 | 82.3 | 42.4 | 74.3 | 39.2 |
| 0.511 | 54.7 | 30.2 | 81.9 | 42.2 | 73.9 | 39.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarrés, Q.; Hernández-Díaz, D.; Ardanuy, M. Interface Strength and Fiber Content Influence on Corn Stover Fibers Reinforced Bio-Polyethylene Composites Stiffness. Polymers 2021, 13, 768. https://doi.org/10.3390/polym13050768
Tarrés Q, Hernández-Díaz D, Ardanuy M. Interface Strength and Fiber Content Influence on Corn Stover Fibers Reinforced Bio-Polyethylene Composites Stiffness. Polymers. 2021; 13(5):768. https://doi.org/10.3390/polym13050768
Chicago/Turabian StyleTarrés, Quim, David Hernández-Díaz, and Mònica Ardanuy. 2021. "Interface Strength and Fiber Content Influence on Corn Stover Fibers Reinforced Bio-Polyethylene Composites Stiffness" Polymers 13, no. 5: 768. https://doi.org/10.3390/polym13050768
APA StyleTarrés, Q., Hernández-Díaz, D., & Ardanuy, M. (2021). Interface Strength and Fiber Content Influence on Corn Stover Fibers Reinforced Bio-Polyethylene Composites Stiffness. Polymers, 13(5), 768. https://doi.org/10.3390/polym13050768