Polymer Adsorbents vs. Functionalized Oxides and Carbons: Particulate Morphology and Textural and SurfaceCharacteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
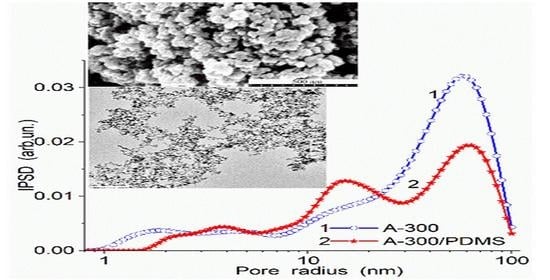
3. Results and Discussion
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iler, R.K. The Chemistry of Silica; Wiley: Chichester, UK, 1979. [Google Scholar]
- Legrand, A.P. (Ed.) The Surface Properties of Silicas; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surface, 6th ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Blitz, J.P.; Little, C. (Eds.) Fundamental and Applied Aspects of Chemically Modified Surfaces; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Rodriguez-Reinoso, F.; McEnaney, B.; Rouquerol, J.; Unger, K. (Eds.) Characterisation of Porous Solids VI. Studies in Surface Science and Catalysis; Elsevier Science: Amsterdam, The Netherlands, 2002; Volume 144. [Google Scholar]
- Somasundaran, P. (Ed.) Encyclopedia of Surface and Colloid Science, 3rd ed.; Taylor & Francis, CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Blitz, J.P.; Gun’ko, V.M. (Eds.) Surface Chemistry in Biomedical and Environmental Science; NATO Science Series II: Mathematics, Physics and Chemistry; Springer: Dordrecht, The Netherlands, 2006; Volume 228. [Google Scholar]
- Shpak, A.P.; Gorbyk, P.P. (Eds.) Nanomaterials and Supramolecular Structures; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Majka, T.; Pielichowski, K. (Eds.) Polymer Composites with Functionalized Nanoparticles. Synthesis, Interactions, Properties and Applications; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Auner, N.; Weis, J. (Eds.) Organosilicon Chemistry VI: From Molecules to Materials; Wiley: Weinheim, Germany, 2005. [Google Scholar]
- Bergna, H.E. (Ed.) Colloidal Silica: Fundamentals and Applications; Taylor & Francis LLC: Salisbury, UK, 2005. [Google Scholar]
- Sprenger, S. Nanosilica-toughened epoxy resins. Polymers 2020, 12, 1777. [Google Scholar] [CrossRef] [PubMed]
- Ismail, A.F.; Goh, P.S. (Eds.) Carbon-Based Polymer Nanocomposites for Environmental and Energy Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Morgan, P. Carbon Fibers and Their Composites; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Dong, Y.; Umer, R.; Lau, A.K.T. (Eds.) Fillers and Reinforcements for Advanced Nanocomposites; Woodhead Publishing: Cambridge, UK, 2015. [Google Scholar]
- Vajtai, R. (Ed.) Springer Handbook of Nanomaterials; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sivasankaran, S. (Ed.) Nanocomposites—Recent Evolutions; IntechOpen: London, UK, 2019. [Google Scholar]
- Lee, B.-S.; Yu, W.-R. Electrospun carbon nanofibers as a functional composite platform: A review of highly tunable microstructures and morphologies for versatile applications. Funct. Compos. Struct. 2020, 2, 012001. [Google Scholar] [CrossRef] [Green Version]
- Ates, M.; Eker, A.A.; Eker, B. Carbon nanotube-based nanocomposites and their applications. J. Adhes. Sci. Technol. 2017, 4243, 1–21. [Google Scholar] [CrossRef]
- Feng, L.; Xie, N.; Zhong, J. Carbon nanofibers and their composites: A review of synthesizing, properties and applications. Materials 2014, 7, 3919–3945. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Zhou, B.; Fernando, K.A.S.; Liu, P.; Allard, L.F.; Sun, Y.-P. Polymeric carbon nanocomposites from carbon nanotubes functionalized with matrix polymer. Macromolecules 2003, 36, 7199–7204. [Google Scholar] [CrossRef]
- Diez-Pascual, A.M. Carbon-based polymer nanocomposites for high-performance applications. Polymers 2020, 12, 872. [Google Scholar] [CrossRef] [Green Version]
- Diez-Pascual, A.M.; Luceño-Sanchez, J.A.; Peña-Capilla, R.; Garcia-Diaz, P. Recent developments in graphene/polymer nanocomposites for application in polymer solar cells. Polymers 2018, 10, 217. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Zhao, Z.; Fu, S.; Meng, L.; Liu, Y.; Chen, F.; Wang, K.; Fu, Q. Fabrication of PLA/CNC/CNT conductive composites for high electromagnetic interference shielding based on pickering emulsions method. Compos. Part A 2019, 125, 105558. [Google Scholar] [CrossRef]
- Ambika; Singh, P.P. Carbon nanocomposites: The potential heterogeneous catalysts for organic transformations. Curr. Org. Chem. 2021, 25, 332. [Google Scholar] [CrossRef]
- Chuiko, A.A. (Ed.) Chemistry of Silica Surface; UkrINTEI: Kiev, Ukraine, 2001. (In Russian) [Google Scholar]
- Henderson, M.A. Interaction of water with solid surfaces: Fundamental aspects revisited. Surf. Sci. Rep. 2002, 46, 1–308. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Turov, V.V. Nuclear Magnetic Resonance Studies of Interfacial Phenomena; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Birdi, K.S. (Ed.) Handbook of Surface and Colloid Chemistry, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Al-Abadleh, H.A.; Grassian, V.H. Oxide surfaces as environmental interfaces. Surf. Sci. Rep. 2003, 52, 63–161. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Leboda, R.; Skubiszewska-Zięba, J.; Gawdzik, B.; Charmas, B. Structural characteristics of porous polymers treated by freezing with water or acetone. Appl. Surf. Sci. 2005, 252, 612–618. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Turov, V.V.; Zarko, V.I.; Goncharuk, O.V.; Pakhlov, E.M.; Skubiszewska-Zięba, J.; Blitz, J.P. Interfacial phenomena at a surface of individual and complex fumed nanooxides. Adv. Colloid Interface Sci. 2016, 235, 108–189. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, Y.; Wang, Y.A.N.; Jiang, G.; Liang, M.; Chen, X.; Long, G. A fractal model for Kozeny—Carman constant and dimensionless permeability of fibrous porous media with roughened surfaces of fibrous porous media with roughened. Fractals 2019, 27, 1–12. [Google Scholar] [CrossRef]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Nee, A.Y.C. (Ed.) Handbook of Manufacturing Engineering and Technology, 1st ed.; Springer: London, UK, 2015. [Google Scholar]
- Mittal, V. (Ed.) Polymer Nanocomposites by Emulsion and Suspension Polymerization, 1st ed.; Royal Society of Chemistry: London, UK, 2011. [Google Scholar]
- Ducheyne, P.; Healy, K.; Hutmacher, D.W.; Grainger, D.W.; Kirkpatrick, C.J. (Eds.) Comprehensive Biomaterials II, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Feldman, D. Polymer nanocomposites in medicine. J. Macromol. Sci. Part A 2016, 53, 55–62. [Google Scholar] [CrossRef]
- Koerner, H.; Drummy, L.F.; Benicewicz, B.; Li, Y.; Vaia, R.A. Nonisotropic self-organization of single-component hairy nanoparticle assemblies. ACS Macro Lett. 2013, 2, 670–676. [Google Scholar] [CrossRef]
- Ethier, J.G.; Hall, L.M. Structure and entanglement network of model polymer-grafted nanoparticle monolayers. Macromolecules 2018, 51, 9878–9889. [Google Scholar] [CrossRef]
- Kim, Y.-G.; Wagner, M.; Thérien-Aubin, H. Dynamics of soft and hairy polymer nanoparticles in a suspension by NMR relaxation. Macromolecules 2020, 53, 844–851. [Google Scholar] [CrossRef] [Green Version]
- Wichaita, W.; Kim, Y.-G.; Tangboriboonrat, P.; Thérien-Aubin, H. Polymer-functionalized polymer nanoparticles and their behaviour in suspensions. Polym. Chem. 2020, 11, 2119–2128. [Google Scholar] [CrossRef]
- Bratek-Skicki, A. Towards a new class of stimuli-responsive polymer-based materials—Recent advances and challenges. Appl. Surf. Sci. Adv. 2021, 4, 100068. [Google Scholar] [CrossRef]
- Richter, D.; Kruteva, M. Polymer dynamics under confinement. Soft Matter 2019, 15, 7316–7349. [Google Scholar] [CrossRef]
- Hore, M.J.A. Polymers on nanoparticles: Structure & dynamics. Soft Matter 2019, 15, 1120–1134. [Google Scholar]
- Vogiatzis, G.G.; Theodorou, D.N. Structure of polymer layers grafted to nanoparticles in silica-polystyrene nanocomposites. Macromolecules 2013, 46, 4670–4683. [Google Scholar] [CrossRef] [Green Version]
- Askar, S.; Li, L.; Torkelson, J.M. Polystyrene-grafted silica nanoparticles: Investigating the molecular weight dependence of glass transition and fragility behavior. Macromolecules 2017, 50, 1589–1598. [Google Scholar] [CrossRef]
- Chen, X. Preparation and property of TiO2 nanoparticle dispersed polyvinyl alcohol composite materials. J. Mater. Sci. Lett. 2002, 21, 1637–1639. [Google Scholar] [CrossRef]
- Yellampalli, S. (Ed.) Carbon Nanotubes Polymer Nanocomposites, 1st ed.; Intech: Rijeka, Croatia, 2011. [Google Scholar]
- Gonzalez, J.A.; Villanueva, M.E.; Piehl, L.L.; Copello, G.J. Development of a chitin/graphene oxide hybrid composite for the removal of pollutant dyes: Adsorption and desorption study. Chem. Eng. J. 2015, 280, 41–48. [Google Scholar] [CrossRef]
- Kashyap, S.; Pratihar, S.K.; Behera, S.K. Strong and ductile graphene oxide reinforced PVA nanocomposites. J. Alloys Compd. 2016, 684, 254–260. [Google Scholar] [CrossRef]
- Yarlagadda, V.; Carpenter, M.K.; Moylan, T.E.; Kukreja, R.S.; Koestner, R.; Gu, W.; Thompson, L.; Kongkanand, A. Boosting fuel cell performance with accessible carbon mesopores. ACS Energy Lett. 2018, 3, 618–621. [Google Scholar] [CrossRef] [Green Version]
- Fairén-Jiménez, D.; Carrasco-Marín, F.; Djurado, D.; Bley, F.; Ehrburger-Dolle, F.; Moreno-Castilla, C. Surface area and microporosity of carbon aerogels from gas adsorption and small- and wide-angle X-ray scattering measurements. J. Phys. Chem. B 2006, 110, 8681–8688. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Meikle, S.T.; Kozynchenko, O.P.; Tennison, S.R.; Ehrburger-Dolle, F.; Morfin, I.; Mikhalovsky, S.V. Comparative characterization of carbon and polymer adsorbents by SAXS and nitrogen adsorption methods. J. Phys. Chem. C 2011, 115, 10727–10735. [Google Scholar] [CrossRef]
- Goliszek, M.; Podkościelna, B.; Fila, K.; Riazanova, A.V.; Aminzadeh, S.; Sevastyanova, O.; Gun’ko, V.M. Synthesis and structure characterization of polymeric nanoporous microspheres with lignin. Cellulose 2018, 25, 5843–5862. [Google Scholar] [CrossRef] [Green Version]
- Sternik, D.; Galaburda, M.V.; Bogatyrov, V.M.; Oranska, O.I.; Charmas, B.; Gun’ko, V.M. Novel porous carbon/clay nanocomposites derived from kaolinite/resorcinol-formaldehyde polymer blends: Synthesis, structure and sorption properties. Appl. Surf. Sci. 2020, 525, 146361. [Google Scholar] [CrossRef]
- Ares, A.E. (Ed.) X-ray Scattering; InTech: Rijeka, Croatia, 2017. [Google Scholar]
- Sztucki, M.; Narayanan, T. Development of an ultra-small-angle X-ray scattering instrument for probing the microstructure and the dynamics of soft matter. J. Appl. Crystallogr. 2007, 40, s459–s462. [Google Scholar] [CrossRef] [Green Version]
- Fultz, B.; Howe, J. Transmission Electron Microscopy and Diffractometry of Materials; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Cullity, B.D.; Stock, S.R. Elements of X-ray Diffraction, 3rd ed.; Prentice-Hall Inc.: New York, NY, USA, 2001. [Google Scholar]
- David, W.I.F.; Shankland, K.; McCusker, L.B.; Baerlocher, C. Structure Determination form Powder Diffraction Data; Oxford Science: London, UK, 2002. [Google Scholar]
- Mai, Y.-W.; Yu, Z.-Z. Polymer Nanocomposites; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Aksnes, D.W.; Førland, K.; Kimtys, L. Pore size distribution in mesoporous materials as studied by 1H NMR. Phys. Chem. Chem. Phys. 2001, 3, 3203–3207. [Google Scholar] [CrossRef]
- Mitchell, J.; Webber, J.B.W.; Strange, J.H. Nuclear magnetic resonance cryoporometry. Phys. Rep. 2008, 461, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Shapiro, Y.E. Structure and dynamics of hydrogels and organogels: An NMR spectroscopy approach. Prog. Polymer Sci. 2011, 36, 1184–1253. [Google Scholar] [CrossRef]
- Landry, M.R. Thermoporometry by differential scanning calorimetry: Experimental considerations and applications. Thermochim. Acta 2005, 433, 27–50. [Google Scholar] [CrossRef]
- Naito, S.; Koyanagi, J.; Komukai, T.; Uno, T. Analysis of three-phase structure of epoxy resin/CNT/graphene by molecular simulation. Polymers 2020, 12, 1821. [Google Scholar] [CrossRef]
- Kwon, J.; Jung, H.; Jung, H.; Lee, J. Micro/nanostructured coating for cotton textiles that repel oil, water, and chemical warfare agents. Polymers 2020, 12, 1826. [Google Scholar] [CrossRef]
- Xu, E.; Zhang, Y.; Lin, L. Improvement of mechanical, hydrophobicity and thermal properties of Chinese fir wood by impregnation of nano silica sol. Polymers 2020, 12, 1632. [Google Scholar] [CrossRef] [PubMed]
- Hong, T.; Jeong, S.-M.; Choi, Y.K.; Lim, T.; Ju, S. Superhydrophobic, elastic, and conducting polyurethane-carbon nanotube–silane–aerogel composite microfiber. Polymers 2020, 12, 1772. [Google Scholar] [CrossRef] [PubMed]
- Rollo, G.; Ronca, A.; Cerruti, P.; Gan, X.P.; Fei, G.; Xia, H.; Gorokhov, G.; Bychanok, D.; Kuzhir, P.; Marino Lavorgna, M.; et al. On the synergistic effect of multi-walled carbon nanotubes and graphene nanoplatelets to enhance the functional properties of SLS 3D-printed elastomeric structures. Polymers 2020, 12, 1841. [Google Scholar] [CrossRef]
- Erdal, N.B.; Lando, G.A.; Yadav, A.; Srivastava, R.K.; Hakkarainen, M. Hydrolytic degradation of porous crosslinked poly(ε-caprolactone) synthesized by high internal phase emulsion templating. Polymers 2020, 12, 1849. [Google Scholar] [CrossRef] [PubMed]
- Jeon, B.; Ha, T.; Lee, D.Y.; Choi, M.-S.; Lee, S.W.; Jung, K.-H. Preparation and electrochemical properties of porous carbon nanofiber electrodes derived from new precursor polymer: 6FDA-TFMB. Polymers 2020, 12, 1851. [Google Scholar] [CrossRef]
- Savina, I.N.; Gun’ko, V.M.; Turov, V.V.; Dainiak, M.; Galaev, I.Y.; Phillips, G.J.; Mikhalovsky, S.V. Porous structure and water state in cross-linked polymer and protein cryo-hydrogels. Soft Matter 2011, 7, 4276–4283. [Google Scholar] [CrossRef]
- Sulym, I.Y.; Klonos, P.; Borysenko, M.V.; Pissis, P.; Gun’ko, V.M. Dielectric and thermal studies of segmental dynamic in silica/PDMS and silica/titania/PDMS nanocomposites. J. Appl. Polym. Sci. 2014, 131, 41154. [Google Scholar] [CrossRef]
- Tomaszewski, W.; Gun’ko, V.M.; Leboda, R.; Skubiszewska-Zięba, J. Interaction of methoxy- and methylenedioxyamphetamines with carbon and polymeric adsorbents in polar liquids. Cent. Eur. J. Chem. 2010, 8, 750–757. [Google Scholar] [CrossRef] [Green Version]
- Stamatopoulou, C.; Klonos, P.; Bondaruk, O.; Koutsoumpis, S.; Gun’ko, V.; Pissis, P.; Karabanova, L. Hydrophilic nanocomposites based on polyurethane/poly(2-hydroxyethyl methacrylate) semi-IPNs and modified/unmodified nanosilica for biomedical applications. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 397–408. [Google Scholar] [CrossRef]
- Klonos, P.; Sulym, I.Y.; Kyriakos, K.; Vangelidis, I.; Zidropoulos, S.; Sternik, D.; Borysenko, M.V.; Kyritsis, A.; Deryło-Marczewska, A.; Gun’ko, V.M.; et al. Interfacial phenomena in core–shell nanocomposites of PDMS adsorbed onto low specific surface area fumed silica nanooxides: Effects of surface modifications. Polymer 2015, 68, 158–167. [Google Scholar] [CrossRef]
- Klonos, P.; Sulym, I.Y.; Sternik, D.; Konstantinou, P.; Goncharuk, O.V.; Deryło–Marczewska, A.; Gun’ko, V.M.; Kyritsis, A.; Pissis, P. Morphology, crysallization and rigid amorphous fraction in PDMS adsorbed onto carbon nanotubes and graphite. Polymer 2018, 139, 130–144. [Google Scholar] [CrossRef]
- Tomaszewski, W.; Gun’ko, V.M.; Skubiszewska-Zięba, J. Solid phase extraction of explosive nitramines on macroreticular polymers modified by freezing with water or acetone. J. Sep. Sci. 2016, 39, 1524–1532. [Google Scholar] [CrossRef] [PubMed]
- Klonos, P.; Kulyk, K.; Borysenko, M.; Gun’ko, V.M.; Kyritsis, A.; Pissis, P. Effects of molecular weight below the entanglement threshold on interfacial nanoparticles/polymer dynamics. Macromolecules 2016, 49, 9457–9473. [Google Scholar] [CrossRef]
- Podkościelna, B.; Gordobil, O.; Riazanova, A.V.; Dobele, G.; Labidi, J.; Lindström, M.; Gun’ko, V.M.; Sevastyanova, O. Novel porous polymeric materials obtained from methacrylic derivatives of lignin copolymerized with styrene and divinylbenzene. ChemistrySelect 2017, 2, 2257–2264. [Google Scholar] [CrossRef]
- Sulym, I.; Goncharuk, O.; Sternik, D.; Terpilowski, K.; Derylo-Marczewska, A.; Borysenko, M.V.; Gun’ko, V.M. Nanooxide/polymer composites with silica@PDMS and ceria-zirconia-silica@PDMS: Textural, morphological and hydrophilic/hydrophobic features. Nanoscale Res. Lett. 2017, 12, 152. [Google Scholar] [CrossRef] [Green Version]
- Gun’ko, V.M.; Pakhlov, E.M.; Goncharuk, O.V.; Andriyko, L.S.; Nychiporuk, Y.M.; Balakin, D.Y.; Sternik, D.; Derylo-Marczewska, A. Nanosilica modified by polydimethylsiloxane depolymerized and chemically bound to nanoparticles or physically bound to unmodified or modified surfaces: Structure and interfacial phenomena. J. Colloid Interface Sci. 2018, 529, 273–282. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Savina, I.N.; Mikhalovsky, S.V. Cryogels: Morphological, structural and adsorption characterisation. Adv. Colloid Interface Sci. 2013, 187–188, 1–46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gun’ko, V.M.; Savina, I.N.; Mikhalovsky, S.V. Properties of water bound in hydrogels. Gels 2017, 3, 37. [Google Scholar] [CrossRef]
- Gun’ko, V.M. Composite materials: Textural characteristics. Appl. Surf. Sci. 2014, 307, 444–454. [Google Scholar] [CrossRef]
- Moreno, Y.P.; da Silva, W.L.; Stedile, F.C.; Radtke, C.; dos Santos, J.H.Z. Micro and nanodomains on structured silica/titania photocatalysts surface evaluated in RhB degradation: Effect of structural properties on catalytic efficiency. Appl. Surf. Sci. Adv. 2021, 3, 100055. [Google Scholar] [CrossRef]
- Gun’ko, V.M. Nano/meso/macroporous materials characterization affected by experimental conditions and features of the used methods. Chem. Phys. Technol. Surf. 2020, 11, 5–24. [Google Scholar] [CrossRef] [Green Version]
- Gun’ko, V.M. Textural characteristics of composite adsorbents analyzed with density functional theory and self-consistent regularization procedure. Chem. Phys. Technol. Surf. 2020, 11, 163–174. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Oranska, O.I.; Paientko, V.V.; Sulym, I.Y. Particulate morphology of nanostructured materials. Chem. Phys. Technol. Surf. 2020, 11, 368–378. [Google Scholar] [CrossRef]
- Provencher, S.W. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comp. Phys. Comm. 1982, 27, 213–227. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez–Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Bergna, H.E.; Roberts, W.O. (Eds.) Colloidal Silica: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Tan, K.; Zuluaga, S.; Gong, Q.; Gao, Y.; Nijem, N.; Li, J.; Thonhauser, T.; Chabal, Y.J. Competitive co-adsorption of CO2 with H2O, NH3, SO2, NO, NO2, N2, O2, and CH4 in M-MOF-74 (M = Mg, Co, Ni): The role of hydrogen bonding. Chem. Mater. 2015, 27, 2203–2217. [Google Scholar] [CrossRef] [Green Version]
- Orsikowsky-Sanchez, A.; Plantier, F.; Miqueu, C. Coupled gravimetric, manometric and calorimetric study of CO2, N2 and CH4 adsorption on zeolites for the assessment of classical equilibrium models. Adsorption 2020, 26, 1137–1152. [Google Scholar] [CrossRef]
- ImageJ. Available online: https://imagej.nih.gov/ij/plugins/granulometry.html (accessed on 23 October 2020).
- Fiji. 2021. Available online: https://imagej.net/Local_Thickness (accessed on 23 October 2020).
- Leboda, R.; Gun’ko, V.M.; Tomaszewski, W.; Trznadel, B.J. Relationship between structural characteristics of activated carbons and their concentrating efficiency with respect to nitroorganics. J. Colloid Interface Sci. 2001, 238, 489–500. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Gun’ko, V.M.; Howell, C.A.; Sandeman, S.R.; Phillips, G.J.; Kozynchenko, O.P.; Tennison, S.R.; Ivanov, A.E.; Mikhalovsky, S.V. Composites with macroporous poly(vinyl alcohol) cryogels with attached activated carbon microparticles with controlled accessibility of a surface. ACS Appl. Mater. Interfaces 2012, 4, 5936–5944. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Turov, V.V.; Krupska, T.V.; Protsak, I.S.; Borysenko, M.V.; Pakhlov, E.M. Polymethylsiloxane alone and in composition with nanosilica under various conditions. J. Colloid Interface Sci. 2019, 541, 213–225. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Gong, X.; He, S. Highly durable superhydrophobic polydimethylsiloxane/silica nanocomposite surfaces with good self-cleaning ability. ACS Omega 2020, 5, 4100–4108. [Google Scholar] [CrossRef]
- Gu, H.; Zhang, Q.; Gu, J.; Li, N.; Xiong, J. Facile preparation of superhydrophobic silica nanoparticles by hydrothermal-assisted sol–gel process and effects of hydrothermal time on surface modification. J. Sol. Gel Sci. Technol. 2018, 87, 478–485. [Google Scholar] [CrossRef]
- Sun, X.L.; Fan, Z.P.; Zhang, L.D.; Wang, L.; Wei, Z.J.; Wang, X.Q.; Liu, W.L. Superhydrophobicity of silica nanoparticles modified with polystyrene. Appl. Surf. Sci. 2011, 257, 2308–2312. [Google Scholar] [CrossRef]
- Gurav, A.B.; Xu, Q.; Latthe, S.S.; Vhatkar, R.S.; Liu, S.; Yoon, H.; Yoon, S.S. Superhydrophobic coatings prepared from methyl-modified silica particles using simple dip-coating method. Ceram. Int. B 2015, 41, 3017–3023. [Google Scholar] [CrossRef]
- Stewart, J.J.P. MOPAC2016. Stewart Computational Chemistry. Available online: http://openmopac.net (accessed on 21 February 2021).
- Stewart, J.J.P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Mod. 2013, 19, 1–32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kothalawala, N.; Blitz, J.P.; Gun’ko, V.M.; Jaroniec, M.; Grabicka, B.; Semeniuc, R.F. Post-synthesis surface modified silicas as adsorbents for heavy metal ion contaminants Cd(II), Cu(II), Cr(III), and Sr(II) in aqueous solutions. J. Colloid Interface Sci. 2013, 392, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Blitz, I.P.; Blitz, J.P.; Gun’ko, V.M.; Sheeran, D.J. Functionalized silicas: Structural characteristics and adsorption of Cu(II) and Pb(II). Colloids Surf. A Physicochem. Eng. Asp. 2007, 307, 83–92. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Turov, V.V.; Zarko, V.I.; Nychiporuk, Y.M.; Goncharuk, E.V.; Pakhlov, E.M.; Yurchenko, G.R.; Kulik, T.V.; Palyanytsya, B.B.; Borodavka, T.V.; et al. Structural features of polymer adsorbent LiChrolut EN and interfacial behavior of water and water-organic mixtures. J. Colloid Interface Sci. 2008, 323, 6–17. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-Y.; Meng, X.; Pu, Y.; Ragauskas, A.J. Recent advances in the application of functionalized lignin in value-added polymeric materials. Polymers 2020, 12, 2277. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Takkellapati, S. The current and emerging sources of technical lignins and their applications. Biofuel. Bioprod. Biorefin. 2018, 12, 756–787. [Google Scholar] [CrossRef]
- Bolze, J.; Kogan, V.; Beckers, D.; Fransen, M. High-performance small- and wide-angle X-ray scattering (SAXS/WAXS) experiments on a multi-functional laboratory goniometer platform with easily exchangeable X-ray modules. Rev. Sci. Instrum. 2018, 89, 085115. [Google Scholar] [CrossRef]
- Kim, Y.; Wichaita, W.; Thérien-Aubin, H. Influence of the architecture of soft polymer-functionalized polymer nanoparticles on their dynamics in suspension. Polymers 2020, 12, 1844. [Google Scholar] [CrossRef]
- Ghosh, S.; Das, S.; Mosquera, M.E.G. Conducting polymer-based nanohybrids for fuel cell application. Polymers 2020, 12, 2993. [Google Scholar] [CrossRef] [PubMed]
- EL-Ghoul, Y.; Ammar, C.; Alminderej, F.M.; Shafiquzzama, M. Design and evaluation of a new natural multi-layered biopolymeric adsorbent system-based chitosan/cellulosic nonwoven material for the biosorption of industrial textile effluents. Polymers 2021, 13, 322. [Google Scholar] [CrossRef] [PubMed]
- Torres-Ávalos, J.A.; Cajero-Zul, L.R.; Milton, V.-L.; López-Dellamary, F.A.; Antonio Martínez-Richa, A.; Barrera-Rivera, K.A.; Francisco, L.-S.; Nuño-Donlucas, S.M. Synthesis of poly(methacrylic acid-co-butyl acrylate) grafted onto functionalized carbon nanotube nanocomposites for drug delivery. Polymers 2021, 13, 533. [Google Scholar] [CrossRef] [PubMed]
- Power, A.J.; Remediakis, I.N.; Harmandaris, V. Interface and interphase in polymer nanocomposites with bare and core-shell gold nanoparticles. Polymers 2021, 13, 541. [Google Scholar] [CrossRef]
- Cho, B.-G.; Joshi, S.R.; Lee, S.; Kim, S.-K.; Park, Y.-B.; Kim, G.-H. Enhanced mechanical and antibacterial properties of nanocomposites based on poly(vinyl alcohol) and biopolymer-derived reduced graphene oxide. Polymers 2021, 13, 615. [Google Scholar] [CrossRef]
- Orellana, J.; Moreno-Villoslada, I.; Bose, R.K.; Picchioni, F.; Flores, M.E.; Araya-Hermosilla, R. Self-healing polymer nanocomposite materials by Joule effect. Polymers 2021, 13, 649. [Google Scholar] [CrossRef] [PubMed]
- Cisneros, C.G.; Bloemen, V.; Mignon, A. Synthetic, natural, and semisynthetic polymer carriers for controlled nitric oxide release in dermal applications: A review. Polymers 2021, 13, 760. [Google Scholar] [CrossRef] [PubMed]
- Bifulco, A.; Marotta, A.; Passaro, J.; Costantini, A.; Cerruti, P.; Gentile, G.; Ambrogi, V.; Malucelli, G.; Branda, F. Thermal and fire behavior of a bio-based epoxy/silica hybrid cured with methyl nadic anhydride. Polymers 2020, 12, 1661. [Google Scholar] [CrossRef] [PubMed]
- Gun’ko, V.M.; Skubiszewska-Zięba, J.; Leboda, R.; Voronin, E.F.; Zarko, V.I.; Levitskaya, S.I.; Brei, V.V.; Guzenko, N.V.; Kazakova, O.A.; Seledets, O.; et al. Pyrocarbons prepared by carbonisation of polymers adsorbed or synthesised on a surface of silica and mixed oxides. Appl. Surf. Sci. 2004, 227, 219–243. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Leboda, R.; Skubiszewska-Zięba, J.; Goncharuk, E.V.; Nychiporuk, Y.M.; Zarko, V.I.; Blitz, J.P. Influence of different treatments on characteristics of nanooxide powders alone or with adsorbed polar polymers or proteins. Powder Technol. 2008, 187, 146–158. [Google Scholar] [CrossRef]
- Turov, V.V.; Turova, A.A.; Goncharuk, E.V.; Gun’ko, V.M. Adsorption of methane with the presence of water on oxide, polymer and carbon adsorbents studied using 1H NMR spectroscopy at low temperatures. Appl. Surf. Sci. 2008, 255, 3310–3317. [Google Scholar] [CrossRef]
- Vilarrasa-García, E.; Cecilia, J.A.; Bastos-Neto, M.; Cavalcante, C.L., Jr.; Azevedo, D.C.S.; Rodriguez-Castellón, E. CO2/CH4 adsorption separation process using pore expanded mesoporous silicas functionalizated by APTES grafting. Adsorption 2015, 21, 565–575. [Google Scholar] [CrossRef]
- Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Weinheim, Germany, 2008.
- Wyman, E.B.; Skief, M.C. (Eds.) Organosilanes Properties Performance and Applications; Nova Science Publishers: New York, NY, USA, 2010. [Google Scholar]
- Buschow, K.H.J. Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998. [Google Scholar]
- Butt, H.-J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces; Wiley-VCH Verlag: Weinheim, Germany, 2003. [Google Scholar]
- Rouquerol, J.; Rouquerol, F.; Sing, K.S.W.; Llewellyn, P.; Maurin, G. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications; Academic Press: London, UK, 2014. [Google Scholar]
- Chang, R. Physical Chemistry for the Biosciences; Edwards Brothers, Inc.: Sausalito, CA, USA, 2005. [Google Scholar]
- Gun’ko, V.M.; Pakhlov, E.M.; Skubiszewska-Zięba, J.; Blitz, J.P. Infrared spectroscopy as a tool for textural and structural characterization of individual and complex fumed oxides. Vib. Spectrosc. 2017, 88, 56–62. [Google Scholar] [CrossRef]














| Sample | SBET (m2/g) | SDFT (m2/g) | Snano (m2/g) | Smeso (m2/g) | Smacro (m2/g) | Vp (cm3/g) | Vnano (cm3/g) | Vmeso (cm3/g) | Vmacro (cm3/g) | <RV> (nm) | <RS> (nm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PMS | 507 | 471 | 2 | 504 | 1 | 1.320 | 0.002 | 1.304 | 0.014 | 6.08 | 5.28 |
| Stirred PMS | 572 | 581 | 1 | 558 | 13 | 2.604 | 0.001 | 2.248 | 0.355 | 16.86 | 9.42 |
| PMS/A-300 | 354 | 322 | 35 | 306 | 13 | 1.265 | 0.019 | 1.084 | 0.163 | 15.25 | 7.64 |
| cPMS/A-300 | 407 | 357 | 8 | 399 | 1 | 1.021 | 0.006 | 1.005 | 0.011 | 6.56 | 5.17 |
| A-300 | 294 | 289 | 44 | 229 | 16 | 0.850 | 0.023 | 0.567 | 0.259 | 20.41 | 6.14 |
| Silica | Modifier | SBET (m2/g) | Vp (cm3/g) |
|---|---|---|---|
| 200DF | - | 484 | 0.31 |
| 200DF | APTS | 28 | 0.06 |
| 200DF | Triamine | 2 | 0.002 |
| 200DF | EDTA | 178 | 0.25 |
| HP39 | - | 449 | 1.96 |
| HP39 | EDTA | 246 | 0.81 |
| SBA-15 | - | 577 | 1.34 |
| SBA-15 | EDTA | 286 | 0.89 |
| Sample | SBET (m2/g) | Snano (m2/g) | Smeso (m2/g) | Smacro (m2/g) | Vp (cm3/g) | Vnano (cm3/g) | Vmeso (cm3/g) | Vmacro (cm3/g) | Δwcyl | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AcSp a | 93 | - | 9 | 80 | 4 | 0.252 | - | 0.004 | 0.207 | 0.069 | 0.030 |
| AcSp b | 86 | −8.3 | 21 | 63 | 3 | 0.231 | −7.5 | 0.007 | 0.190 | 0.058 | −0.051 |
| AcSp c | 85 | −2.7 | 22 | 61 | 3 | 0.220 | −8.6 | 0.007 | 0.184 | 0.058 | −0.055 |
| XAD-7 a | 341 | - | 72 | 269 | - | 0.440 | - | 0.030 | 0.409 | 0.002 | 0.041 |
| XAD-7 b | 462 | 35.5 | 108 | 321 | 33 | 0.905 | 105.7 | 0.044 | 0.540 | 0.589 | 0.059 |
| XAD-7 c | 488 | 43.1 | 109 | 378 | 1 | 0.798 | 81.4 | 0.044 | 0.767 | 0.015 | 0.054 |
| XAD-16 a | 853 | - | 92 | 751 | 11 | 1.347 | - | 0.029 | 1.247 | 0.170 | 0.148 |
| XAD-16 b | 982 | 15.1 | 119 | 860 | 3 | 1.889 | 40.2 | 0.037 | 1.825 | 0.047 | 0.142 |
| XAD-16 c | 984 | 15.4 | 106 | 876 | 2 | 2.026 | 50.4 | 0.034 | 1.984 | 0.031 | 0.139 |
| Sample | SBET (m2/g) | Vp (cm3/g) | ||
|---|---|---|---|---|
| XAD-7 a | 338 | - | 0.462 | - |
| XAD-7 b | 444 | 31.4 | 0.610 | 32.0 |
| XAD-7 c | 422 | 24.9 | 0.562 | 21.6 |
| XAD-7 d | 466 | 37.9 | 0.623 | 34.8 |
| XAD-7 e | 485 | 43.5 | 0.667 | 44.4 |
| XAD-7 f | 421 | 24.6 | 0.564 | 22.1 |
| XAD-16 a | 836 | - | 1.524 | - |
| XAD-16 b | 932 | 11.5 | 1.824 | 19.7 |
| XAD-16 c | 878 | 5.0 | 1.633 | 7.2 |
| XAD-16 d | 936 | 12.0 | 1.844 | 21.0 |
| XAD-16 f | 937 | 12.1 | 1.824 | 19.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gun’ko, V.M. Polymer Adsorbents vs. Functionalized Oxides and Carbons: Particulate Morphology and Textural and SurfaceCharacteristics. Polymers 2021, 13, 1249. https://doi.org/10.3390/polym13081249
Gun’ko VM. Polymer Adsorbents vs. Functionalized Oxides and Carbons: Particulate Morphology and Textural and SurfaceCharacteristics. Polymers. 2021; 13(8):1249. https://doi.org/10.3390/polym13081249
Chicago/Turabian StyleGun’ko, Volodymyr M. 2021. "Polymer Adsorbents vs. Functionalized Oxides and Carbons: Particulate Morphology and Textural and SurfaceCharacteristics" Polymers 13, no. 8: 1249. https://doi.org/10.3390/polym13081249
APA StyleGun’ko, V. M. (2021). Polymer Adsorbents vs. Functionalized Oxides and Carbons: Particulate Morphology and Textural and SurfaceCharacteristics. Polymers, 13(8), 1249. https://doi.org/10.3390/polym13081249