Thermal Conductivity of Nanoporous Materials: Where Is the Limit?
Abstract
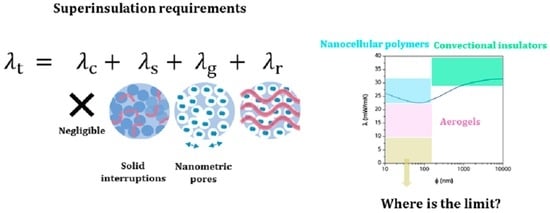
:1. Introduction
2. Thermal Conductivity in Nanoporous Materials
2.1. Measurement Techniques
2.1.1. Transient Methods: Technique Description
2.1.2. Steady-State Methods: Technique Description
2.1.3. Empirical Comparison between Transient and Steady-State Methods
2.2. Thermal Conductivity of Nanocellular Polymers
2.2.1. Nanocellular Polymers
2.2.2. Thermal Conductivity in Nanocellular Polymers
| Material | Bulk Density/ kg/m3 | Cell Size/ nm | Thermal Conductivity/ mW/(m K) | Ref. |
|---|---|---|---|---|
| PMMA/MAM | 420 | 950 | 83.7 | Notario B. et al., 2015 [11] |
| 570 | 820 | 107.2 | ||
| 490 | 300 | 88.4 | ||
| 470 | 290 | 88.4 | ||
| 510 | 235 | 92.5 | ||
| 480 | 220 | 90.0 | ||
| 690 | 200 | 101.5 | ||
| 600 | 150 | 94.8 | ||
| 650 | 130 | 94.7 | ||
| 710 | 94 | 104.3 | ||
| PMMA/TPU | 165 | 930 | 36.9 | Wang G. et al., 2017 [47] |
| 153 | 205 | 24.8 | ||
| PMMA | 486 | 225 | 87.5 | Martín-de León J. et al., 2019 [52] |
| 403 | 79.3 | |||
| 320 | 71.3 | |||
| 249 | 58.8 | |||
| 605 | 25 | 97.0 | ||
| 546 | 89.6 | |||
| 522 | 87.2 | |||
| 510 | 83.9 | |||
| 474 | 79.3 | |||
| 451 | 76.9 | |||
| 415 | 72.4 | |||
| PMMA/MAM (a) | 415 | Bimodal: 258 nm + 2.2 µm (15%) | 83.0 | Bernardo V. et al., 2019 [53] |
| 320 | Bimodal: 276 nm + 2.1 µm (14%) | 70.0 | ||
| PMMA/SEP (a) | 451 | Bimodal: 260 nm + 2.9 µm (30%) | 92.0 | Bernardo V. et al., 2019 [53] |
| 0.29 | Bimodal: 296 nm + 2.1 µm (43%) | 80.0 |
2.3. Thermal Conductivity of Aerogels
2.3.1. Silica Aerogels: Effect of Structural Properties on the Thermal Conductivity
2.3.2. PU-Aerogels: Effect of Structural Properties on the Thermal Conductivity
3. Modeling Thermal Conductivity of Nanoporous Materials
3.1. Radiation Term
3.2. Gaseous Thermal Conductivity
3.3. Solid Thermal Conductivity
3.4. Future Perspectives
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raitt, D. The greatest engineering achievements of the twentieth century. Int. J. Entrep. Behav. Res. 2000, 6. [Google Scholar] [CrossRef]
- Siegrist, M.; Visschers, V.H.M. Acceptance of nuclear power: The Fukushima effect. Energy Policy 2013, 59, 112–119. [Google Scholar] [CrossRef]
- European Commission Energy Efficient Buildings. Available online: https://energy.ec.europa.eu/topics/energy-efficiency/energy-efficient-buildings_en (accessed on 1 May 2022).
- Petter Jelle, B. Nano-Based Thermal Insulation for Energy-Efficient Buildings; Elsevier Ltd.: Amsterdam, The Netherlands, 2016; ISBN 9780081005491. [Google Scholar]
- Lamy-Mendes, A.; Pontinha, A.D.R.; Alves, P.; Santos, P.; Durães, L. Progress in silica aerogel-containing materials for buildings’ thermal insulation. Constr. Build. Mater. 2021, 286, 122815. [Google Scholar] [CrossRef]
- Linhares, T.; Pessoa de Amorim, M.T.; Durães, L. Silica aerogel composites with embedded fibres: A review on their preparation, properties and applications. J. Mater. Chem. A 2019, 7, 22768–22802. [Google Scholar] [CrossRef]
- Wernery, J.; Mancebo, F.; Malfait, W.J.; O’Connor, M.; Jelle, B.P. The economics of thermal superinsulation in buildings. Energy Build. 2021, 253, 111506. [Google Scholar] [CrossRef]
- Stephan, K.; Laesecke, A. The Thermal Conductivity of Fluid Air. J. Phys. Chem. Ref. Data 1985, 14, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Hilyard, N.C.; Cunningham, A. Low Density Cellular Plastics—Physical Basis of Behaviour; Chapman and Hall: London, UK, 1994; ISBN 0412584107. [Google Scholar]
- Notario, B.; Pinto, J.; Solorzano, E.; de Saja, J.A.; Dumon, M.; Rodriguez-Perez, M.A. Experimental validation of the Knudsen effect in nanocellular polymeric foams. Polymer 2015, 56, 57–67. [Google Scholar] [CrossRef]
- Bristow, K.L. Thermal Conductivity. In Methods of Soil Analysis. Part 4 Physical Methods; Soil Science Society of America: Madison, WI, USA, 2002; pp. 1209–1226. [Google Scholar]
- Gomes, M.G.; Flores-Colen, I.; da Silva, F.; Pedroso, M. Thermal conductivity measurement of thermal insulating mortars with EPS and silica aerogel by steady-state and transient methods. Constr. Build. Mater. 2018, 172, 696–705. [Google Scholar] [CrossRef]
- Taylor, R. Thermal Conductivity. Concise Encycl. Adv. Ceram. Mater. 1991, 472–475. [Google Scholar] [CrossRef]
- Asadi, I.; Shafigh, P.; Bin Abu Hassan, Z.F.; Mahyuddin, N.B. Thermal conductivity of concrete—A review. J. Build. Eng. 2018, 20, 81–93. [Google Scholar] [CrossRef]
- Mathis, N. Transient thermal conductivity measurements: Comparison of destructive and nondestructive techniques. High Temp. High Press. 2000, 32, 321–327. [Google Scholar] [CrossRef]
- Solórzano, E.; Rodriguez-Perez, M.A.; de Saja, J.A. Thermal conductivity of cellular metals measured by the transient plane source method. Adv. Eng. Mater. 2008, 10, 596–602. [Google Scholar] [CrossRef]
- Franco, A. An apparatus for the routine measurement of thermal conductivity of materials for building application based on a transient hot-wire method. Appl. Therm. Eng. 2007, 27, 2495–2504. [Google Scholar] [CrossRef]
- Healy, J.J.; de Groot, J.J.; Kestin, J. The theory of the transient hot-wire method for measuring thermal conductivity. Phys. B+C 1976, 82, 392–408. [Google Scholar] [CrossRef]
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- Zheng, Q.; Kaur, S.; Dames, C.; Prasher, R.S. Analysis and improvement of the hot disk transient plane source method for low thermal conductivity materials. Int. J. Heat Mass Transf. 2020, 151, 119331. [Google Scholar] [CrossRef] [Green Version]
- ASTM C518; Standard Test Method for Steady-State Thermal Transmission Properties by Means of the Heat Flow Meter Apparatus. ASTM International: West Conshohocken, PA, USA, 2017.
- UNE-EN 12667:2001; Thermal Performance of Building Materials and Products. Determination of Thermal Resistance by Means of Guarded Hot Plate and Heat Flow Meter Methods. Products of High and Medium thermal resistance. iTeh, Inc.: Newark, NJ, USA, 2002.
- ISO 8302; Thermal Insulation—Determination of Steady-State Thermal Resistance and Related Properties-Guarded Hot Plate Apparatus. iTeh, Inc.: Newark, NJ, USA, 1991.
- ASTM C177; Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus. ASTM International: West Conshohocken, PA, USA, 1997.
- TA Instruments. Available online: https://www.tainstruments.com/?lang=es (accessed on 1 May 2022).
- Yüksel, N. The Review of Some Commonly Used Methods and Techniques to Measure the Thermal Conductivity of Insulation Materials. In Insulation Materials in Context of Sustainability; IntechOpen Limited: London, UK, 2016. [Google Scholar]
- Zhao, D.; Qian, X.; Gu, X.; Jajja, S.A.; Yang, R. Measurement techniques for thermal conductivity and interfacial thermal conductance of bulk and thin film materials. J. Electron. Packag. Trans. ASME 2016, 138, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Jannot, Y.; Degiovanni, A.; Grigorova-Moutiers, V.; Godefroy, J. A passive guard for low thermal conductivity measurement of small samples by the hot plate method. Meas. Sci. Technol. 2017, 28, 015008. [Google Scholar] [CrossRef]
- Vos, B.H. Measurements of thermal conductivity by a non-steady-state method. Appl. Sci. Res. Sect. A 1956, 5, 425–438. [Google Scholar] [CrossRef]
- Jannot, Y.; Schaefer, S.; Degiovanni, A.; Bianchin, J.; Fierro, V.; Celzard, A. A new method for measuring the thermal conductivity of small insulating samples. Rev. Sci. Instrum. 2019, 90, 054901. [Google Scholar] [CrossRef]
- Jannot, Y.; Felix, V.; Degiovanni, A. A centered hot plate method for measurement of thermal properties of thin insulating materials. Meas. Sci. Technol. 2010, 21, 035106. [Google Scholar] [CrossRef]
- Miller, R.A.; Kuczmarski, M.A. Method for measuring thermal conductivity of small highly insulating specimens. J. Test. Eval. 2010, 38, 167–176. [Google Scholar] [CrossRef]
- Sánchez-Calderón, I.; Merillas, B.; Bernardo, V.; Rodríguez-Pérez, M.Á. Methodology for measuring the thermal conductivity of insulating samples with small dimensions by heat flow meter technique. J. Therm. Anal. Calorim. 2022. Unpublished. [Google Scholar]
- Costeux, S. CO2-blown nanocellular foams. J. Appl. Polym. Sci. 2014, 131, 23. [Google Scholar] [CrossRef]
- Notario, B.; Pinto, J.; Rodriguez-Perez, M.A. Nanoporous polymeric materials: A new class of materials with enhanced properties. Prog. Mater. Sci. 2016, 78–79, 93–139. [Google Scholar] [CrossRef] [Green Version]
- Hentze, H.P.; Antonietti, M. Porous polymers and resins for biotechnological and biomedical applications. Rev. Mol. Biotechnol. 2002, 90, 27–53. [Google Scholar] [CrossRef]
- Urbanczyk, L.; Calberg, C.; Detrembleur, C.; Jérôme, C.; Alexandre, M. Batch foaming of SAN/clay nanocomposites with scCO2: A very tunable way of controlling the cellular morphology. Polymer 2010, 51, 3520–3531. [Google Scholar] [CrossRef]
- Martín-de León, J.; Bernardo, V.; Rodríguez-Pérez, M.Á. Nanocellular polymers: The challenge of creating cells in the nanoscale. Materials 2019, 12, 797. [Google Scholar] [CrossRef] [Green Version]
- Okolieocha, C.; Raps, D.; Subramaniam, K.; Altstädt, V. Microcellular to nanocellular polymer foams: Progress (2004-2015) and future directions—A review. Eur. Polym. J. 2015, 73, 500–519. [Google Scholar] [CrossRef]
- León, J.M.; Bernardo, V.; Laguna-Gutiérrez, E.; Rodríguez-Pérez, M.Á. Influence of the viscosity of poly(methyl methacrylate) on the cellular structure of nanocellular materials. Polym. Int. 2020, 69, 72–83. [Google Scholar] [CrossRef]
- Martín-de León, J.; Bernardo, V.; Rodríguez-Pérez, M.Á. Key Production Parameters to Obtain Transparent Nanocellular PMMA. Macromol. Mater. Eng. 2017, 302, 1700343. [Google Scholar] [CrossRef]
- Guo, H.; Kumar, V. Some thermodynamic and kinetic low-temperature properties of the PC-CO2 system and morphological characteristics of solid-state PC nanofoams produced with liquid CO2. Polymer 2015, 56, 46–56. [Google Scholar] [CrossRef]
- Guo, H.; Nicolae, A.; Kumar, V. Fabrication of high temperature polyphenylsulfone nanofoams using high pressure liquid carbon dioxide. Cell. Polym. 2016, 35, 119–142. [Google Scholar] [CrossRef]
- Guo, H.; Nicolae, A.; Kumar, V. Solid-state microcellular and nanocellular polysulfone foams. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 975–985. [Google Scholar] [CrossRef]
- Costeux, S.; Bunker, S.P.; Jeon, H.K. Homogeneous nanocellular foams from styrenic-acrylic polymer blends. J. Mater. Res. 2013, 28, 2351–2365. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, J.; Mark, L.H.; Wang, G.; Yu, K.; Wang, C.; Park, C.B.; Zhao, G. Ultra-tough and super thermal-insulation nanocellular PMMA/TPU. Chem. Eng. J. 2017, 325, 632–646. [Google Scholar] [CrossRef]
- Bernardo, V.; Martin-de Leon, J.; Sanchez-Calderon, I.; Laguna-Gutierrez, E.; Rodriguez-Perez, M.A. Nanocellular Polymers with a Gradient Cellular Structure Based on Poly(methyl methacrylate)/Thermoplastic Polyurethane Blends Produced by Gas Dissolution Foaming. Macromol. Mater. Eng. 2019, 1900428, 1–9. [Google Scholar] [CrossRef]
- Bernardo, V.; Martín-de León, J.; Rodríguez-Pérez, M.Á. Production of PMMA-based nanocellular polymers using low demanding saturation conditions. Mater. Lett. 2019, 255, 126551. [Google Scholar] [CrossRef]
- Bernardo, V. Production and Characterization of Nanocellular Polymers Based on Nanostructured PMMA Blends and PMMA Nanocomposites. Ph.D. Thesis, University of Valladolid, Valladolid, Spain, 2019. [Google Scholar]
- Buahom, P.; Wang, C.; Alshrah, M.; Wang, G.; Gong, P.; Tran, M.-P.; Park, C.B. Wrong expectation of superinsulation behavior from largely-expanded nanocellular foams. Nanoscale 2020, 12, 13064–13085. [Google Scholar] [CrossRef]
- Martin-de Leon, J. Understanding the Production Process of Nanocellular Polymers Based on PMMA Driven by Homogeneous Nucleation. 2019. Available online: https://pdfs.semanticscholar.org/a3d2/2c024e3c550652f34f510769ad3d84e6020d.pdf (accessed on 1 May 2022).
- Bernardo, V.; Martin-de Leon, J.; Pinto, J.; Verdejo, R.; Rodriguez-Perez, M.A. Modeling the heat transfer by conduction of nanocellular polymers with bimodal cellular structures. Polymer 2019, 160, 126–137. [Google Scholar] [CrossRef]
- Kistler, S.S. Coherent Expanded Aerogels and Jellies. Nature 1931, 127, 741. [Google Scholar] [CrossRef]
- Kistler, S.S. Coherent expanded aerogels. J. Phys. Chem. 1932, 36, 52–64. [Google Scholar] [CrossRef]
- Vareda, J.P.; García-González, C.A.; Valente, A.J.M.; Simón-Vázquez, R.; Stipetic, M.; Durães, L. Insights on toxicity, safe handling and disposal of silica aerogels and amorphous nanoparticles. Environ. Sci. Nano 2021, 8, 1177–1195. [Google Scholar] [CrossRef]
- Pierre, A.C.; Rigacci, A. SiO2 Aerogels Alain. In Aerogels Handbook; Springer: Berlin, Germany, 2011; pp. 21–45. ISBN 9781441975898. [Google Scholar]
- Smirnova, I.; Gurikov, P. Aerogel production: Current status, research directions, and future opportunities. J. Supercrit. Fluids 2018, 134, 228–233. [Google Scholar] [CrossRef]
- Duraes, L.; Maleki, H.; Vareda, J.P.; Lamy-Mendes, A.; Portugal, A. Exploring the Versatile Surface Chemistry of Silica Aerogels for Multipurpose Application. MRS Adv. 2017, 2, 3511–3519. [Google Scholar] [CrossRef]
- Maleki, H. Recent advances in aerogels for environmental remediation applications: A review. Chem. Eng. J. 2016, 300, 98–118. [Google Scholar] [CrossRef]
- Maleki, H.; Durães, L.; García-González, C.A.; del Gaudio, P.; Portugal, A.; Mahmoudi, M. Synthesis and biomedical applications of aerogels: Possibilities and challenges. Adv. Colloid Interface Sci. 2016, 236, 1–27. [Google Scholar] [CrossRef]
- Maleki, H.; Hüsing, N. Current status, opportunities and challenges in catalytic and photocatalytic applications of aerogels: Environmental protection aspects. Appl. Catal. B Environ. 2018, 221, 530–555. [Google Scholar] [CrossRef]
- Probst, L.; Frideres, L.; Pedersen, B.; Clarke, S. Aerogels, getting their second wind. Adv. Mater. 2015, 14. Available online: https://docplayer.net/157909313-Advanced-materials-business-innovation-observatory-aerogels-getting-their-second-wind-case-study-56.html (accessed on 1 May 2022).
- Berardi, U. The benefits of using aerogel-enhanced systems in building retrofits. Energy Procedia 2017, 134, 626–635. [Google Scholar] [CrossRef]
- Paola, M.; Francesco, A.; Daniela, V.; Federico, O.; Luca, E.; Claudia, G.; Roberto, D.; Lucia, F.; Gianluca, G.; Paolo, M.; et al. On the Retrofit of Existing Buildings with Aerogel Panels: Energy, Environmental and Economic Issues. Energies 2021, 14, 1276. [Google Scholar]
- Ghica, M.E.; Almeida, C.M.R.; Fonseca, M.; Portugal, A.; Durães, L. Optimization of polyamide pulp-reinforced silica aerogel composites for thermal protection systems. Polymers 2020, 12, 1278. [Google Scholar] [CrossRef] [PubMed]
- Pang, H.Q.; Zhang, R.; Yang, H.L.; Li, Z.Y.; Xu, H.B. Preparation and thermal insulation performance characterization of endothermic opacifier doped silica aerogel. Int. J. Therm. Sci. 2022, 174, 107431. [Google Scholar] [CrossRef]
- Hou, X.; Zhang, R.; Fang, D. An ultralight silica-modified ZrO2–SiO2 aerogel composite with ultra-low thermal conductivity and enhanced mechanical strength. Scr. Mater. 2018, 143, 113–116. [Google Scholar] [CrossRef]
- Torres, R.B.; Vareda, J.P.; Lamy-Mendes, A.; Durães, L. Effect of different silylation agents on the properties of ambient pressure dried and supercritically dried vinyl-modified silica aerogels. J. Supercrit. Fluids 2019, 147, 81–89. [Google Scholar] [CrossRef]
- Pan, Y.; Cheng, X.; zhou, T.; Gong, L.; Zhang, H. Spray freeze-dried monolithic silica aerogel based on water-glass with thermal superinsulating properties. Mater. Lett. 2018, 229, 265–268. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Li, H.; Ji, H.; Sun, X.; He, J. Effect of sepiolite fiber on the structure and properties of the sepiolite/silica aerogel composite. J. Sol-Gel Sci. Technol. 2013, 67, 646–653. [Google Scholar] [CrossRef]
- Zhao, S.; Stojanovic, A.; Angelica, E.; Emery, O.; Rentsch, D.; Pauer, R.; Koebel, M.M.; Malfait, W.J. Phase transfer agents facilitate the production of superinsulating silica aerogel powders by simultaneous hydrophobization and solvent- and ion-exchange. Chem. Eng. J. 2020, 381, 122421. [Google Scholar] [CrossRef]
- Stojanovic, A.; Zhao, S.; Angelica, E.; Malfait, W.J.; Koebel, M.M. Three routes to superinsulating silica aerogel powder. J. Sol-Gel Sci. Technol. 2019, 90, 57–66. [Google Scholar] [CrossRef]
- Liu, R.; Wang, J.; Liao, J.; Zhang, X. Robust Silica–Polyimide Aerogel Blanket for Water-Proof and Flame-Retardant Self-Floating Artificial Island. Front. Mater. 2021, 8, 113. [Google Scholar] [CrossRef]
- Zhao, S.; Emery, O.; Wohlhauser, A.; Koebel, M.M.; Adlhart, C.; Malfait, W.J. Merging flexibility with superinsulation: Machinable, nanofibrous pullulan-silica aerogel composites. Mater. Des. 2018, 160, 294–302. [Google Scholar] [CrossRef]
- Jaxel, J.; Markevicius, G.; Rigacci, A.; Budtova, T. Thermal superinsulating silica aerogels reinforced with short man-made cellulose fibers. Compos. Part A Appl. Sci. Manuf. 2017, 103, 113–121. [Google Scholar] [CrossRef]
- Huber, L.; Zhao, S.; Malfait, W.J.; Vares, S.; Koebel, M.M. Fast and Minimal-Solvent Production of Superinsulating Silica Aerogel Granulate. Angew. Chemie Int. Ed. 2017, 56, 4753–4756. [Google Scholar] [CrossRef]
- Iswar, S.; Snellings, G.M.B.F.; Zhao, S.; Erni, R.; Bahk, Y.K.; Wang, J.; Lattuada, M.; Koebel, M.M.; Malfait, W.J. Reinforced and superinsulating silica aerogel through in situ cross-linking with silane terminated prepolymers. Acta Mater. 2018, 147, 322–328. [Google Scholar] [CrossRef] [Green Version]
- Iswar, S.; Galmarini, S.; Bonanomi, L.; Wernery, J.; Roumeli, E.; Nimalshantha, S.; Ben Ishai, A.M.; Lattuada, M.; Koebel, M.M.; Malfait, W.J. Dense and strong, but superinsulating silica aerogel. Acta Mater. 2021, 213, 116959. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Z.; Sèbe, G.; Wu, R.; Rivera Virtudazo, R.V.; Tingaut, P.; Koebel, M.M. Multiscale assembly of superinsulating silica aerogels within silylated nanocellulosic scaffolds: Improved mechanical properties promoted by nanoscale chemical compatibilization. Adv. Funct. Mater. 2015, 25, 2326–2334. [Google Scholar] [CrossRef]
- Rezaei, S.; Zolali, A.M.; Jalali, A.; Park, C.B. Strong, highly hydrophobic, transparent, and super-insulative polyorganosiloxane-based aerogel. Chem. Eng. J. 2021, 413, 127488. [Google Scholar] [CrossRef]
- Vareda, J.P.; Lamy-Mendes, A.; Durães, L. A reconsideration on the definition of the term aerogel based on current drying trends. Microporous Mesoporous Mater. 2018, 258, 211–216. [Google Scholar] [CrossRef]
- Ebert, H. Thermal Properties of Aerogels. Aerogels Handb. 2011, 537–564. [Google Scholar] [CrossRef]
- Swimm, K.; Reichenauer, G.; Vidi, S.; Ebert, H.P. Impact of thermal coupling effects on the effective thermal conductivity of aerogels. J. Sol-Gel Sci. Technol. 2017, 84, 466–474. [Google Scholar] [CrossRef]
- Swimm, K.; Vidi, S.; Reichenauer, G.; Ebert, H.P. Impact of the Backbone Connectivity on the Gas Pressure-Dependent Thermal Conductivity of Porous Solids. Int. J. Thermophys. 2022, 43, 1–23. [Google Scholar] [CrossRef]
- Tan, C.; Fung, B.M.; Newman, J.K.; Vu, C. Organic aerogels with very high impact strength. Adv. Mater. 2001, 13, 644–646. [Google Scholar] [CrossRef]
- Szycher, M. Szycher’s Handbook of Polyurethanes, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012; ISBN 9781439863138. [Google Scholar]
- Ying-Zhang, X.; Hui-Wang, G.; Liu, D.; Wang, Y. Applications of rigid polyurethane foam insulation materials in architectural energy conservation. Adv. Mater. Res. 2013, 608–609, 1783–1785. [Google Scholar] [CrossRef]
- Kosmela, P.; Hejna, A.; Suchorzewski, J.; Piszczyk, Ł.; Haponiuk, J.T. Study on the structure-property dependences of rigid PUR-PIR foams obtained from marine biomass-based biopolyol. Materials 2020, 13, 1257. [Google Scholar] [CrossRef] [Green Version]
- Gravit, M.; Kuleshin, A.; Khametgalieva, E.; Karakozova, I. Technical characteristics of rigid sprayed PUR and PIR foams used in construction industry. IOP Conf. Ser. Earth Environ. Sci. 2017, 90, 012187. [Google Scholar] [CrossRef] [Green Version]
- Merillas, B.; Villafañe, F.; Rodríguez-Pérez, M.Á. Super-insulating transparent polyisocyanurate-polyurethane aerogels: Analysis of the thermal conductivity and mechanical properties. Under Rev. 2022. SSRN 4075678. [Google Scholar]
- Merillas, B.; Martín-de León, J.; Villafañe, F.; Rodríguez-Pérez, M.Á. Optical Properties of Polyisocyanurate – Polyurethane Aerogels: Study of the Scattering Mechanisms. Nanomaterials 2022, 12, 1522. [Google Scholar] [CrossRef]
- Bang, A.; Buback, C.; Sotiriou-Leventis, C.; Leventis, N. Flexible aerogels from hyperbranched polyurethanes: Probing the role of molecular rigidity with poly(Urethane Acrylates) versus poly(Urethane Norbornenes). Chem. Mater. 2014, 26, 6979–6993. [Google Scholar] [CrossRef]
- Chidambareswarapattar, C.; McCarver, P.M.; Luo, H.; Lu, H.; Sotiriou-Leventis, C.; Leventis, N. Fractal multiscale nanoporous polyurethanes: Flexible to extremely rigid aerogels from multifunctional small molecules. Chem. Mater. 2013, 25, 3205–3224. [Google Scholar] [CrossRef]
- Rigacci, A.; Marechal, J.C.; Repoux, M.; Moreno, M.; Achard, P. Preparation of polyurethane-based aerogels and xerogels for thermal superinsulation. J. Non. Cryst. Solids 2004, 350, 372–378. [Google Scholar] [CrossRef]
- Zhu, Z.; Snellings, G.M.B.F.; Koebel, M.M.; Malfait, W.J. Superinsulating Polyisocyanate Based Aerogels: A Targeted Search for the Optimum Solvent System. ACS Appl. Mater. Interfaces 2017, 9, 18222–18230. [Google Scholar] [CrossRef] [PubMed]
- Diascorn, N.; Calas, S.; Sallée, H.; Achard, P.; Rigacci, A. Polyurethane aerogels synthesis for thermal insulation - textural, thermal and mechanical properties. J. Supercrit. Fluids 2015, 106, 76–84. [Google Scholar] [CrossRef]
- Biesmans, G.; Randall, D.; Francais, E.; Perrut, M. Polyurethane-based organic aerogels’ thermal performance. J. Non. Cryst. Solids 1998, 225, 36–40. [Google Scholar] [CrossRef]
- Zhu, W.; Zheng, G.; Cao, S.; He, H. Thermal conductivity of amorphous SiO2 thin film: A molecular dynamics study. Sci. Rep. 2018, 8, 10537. [Google Scholar] [CrossRef] [Green Version]
- Kong, H. Thermal Conductivity of Polymers (Hansen). Polymer 1977, 18, 984–1004. [Google Scholar]
- Bernardo, V.; Martin-de Leon, J.; Pinto, J.; Schade, U.; Rodriguez-Perez, M.A. On the interaction of infrared radiation and nanocellular polymers: First experimental determination of the extinction coefficient. Colloids Surfaces A Physicochem. Eng. Asp. 2020, 600, 124937. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Aerogel insulation for building applications: A state-of-the-art review. Energy Build. 2011, 43, 761–769. [Google Scholar] [CrossRef] [Green Version]
- Forest, C.; Chaumont, P.; Cassagnau, P.; Swoboda, B.; Sonntag, P. Polymer nano-foams for insulating applications prepared from CO2 foaming. Prog. Polym. Sci. 2015, 41, 122–145. [Google Scholar] [CrossRef]
- Song, S.; Yovanovich, M.M.; Goodman, F.O. Thermal Gap Conductance of Conforming Surfaces in Contact. J. Heat Transfer 1993, 115, 533–540. [Google Scholar] [CrossRef]
- Nassios, J. Kinetic theory of rarefied gas flows with modern applications. Tech. Pap. 2006. Available online: https://austms.org.au/wp-content/uploads/Gazette/2013/Mar13/Nassios.pdf (accessed on 1 May 2022).
- Rashidi, V.; Coyle, E.J.; Sebeck, K.; Kieffer, J.; Pipe, K.P. Thermal Conductance in Cross-linked Polymers: Effects of Non-Bonding Interactions. J. Phys. Chem. B 2017, 121, 4600–4609. [Google Scholar] [CrossRef] [PubMed]
- Feng, T.; He, J.; Rai, A.; Hun, D.; Liu, J.; Shrestha, S.S. Size Effects in the Thermal Conductivity of Amorphous Polymers. Phys. Rev. Appl. 2020, 14, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, Y.; Cheng, Y.; Chen, J.; Li, N.; Zhang, G. Size-dependent phononic thermal transport in low-dimensional nanomaterials. Phys. Rep. 2020, 860, 1–26. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Zhao, J.; Liu, J.; Xia, X.; Wu, X. Thermal conductivity of micro/nano-porous polymers: Prediction models and applications. Front. Phys. 2022, 17, 23202. [Google Scholar] [CrossRef]
- Angel, A.; Suárez, G.; Nino, J. Computational analysis of the thermal behavior on a silica (SiO2) aerogel coating for applications in the construction industry. IOP Conf. Ser. Mater. Sci. Eng. 2019, 519, 012008. [Google Scholar] [CrossRef]
- Martin-de Leon, J.; van Loock, F.; Bernardo, V.; Fleck, N.A.; Rodriguez-Pérez, M.A. The influence of cell size on the mechanical properties of nanocellular PMMA. Polymer 2019, 181, 121805. [Google Scholar] [CrossRef]
- Miller, D.; Kumar, V. Microcellular and nanocellular solid-state polyetherimide (PEI) foams using sub-critical carbon dioxide II. Tensile and impact properties. Polymer 2011, 52, 2910–2919. [Google Scholar] [CrossRef]
- Estravis, S.; Windle, A.H.; van Es, M.; Elliott, J.A. Thermodynamic limits on cell size in the production of stable polymeric nanocellular materials. Polymer 2020, 186, 122036. [Google Scholar] [CrossRef]







| Transient Method | Steady-State Method | |
|---|---|---|
| Type of technique | Derivative | Absolute |
| Power input | Pulsed power | Constant power |
| Accuracy | Low | High |
| Time consuming | Short | Long |
| Sample size | Small | Large |
| Sample | Bulk Density/ kg/m3 | TPS/ mW/(m K) | SD | Steady-State/ mW/(m K) | SD |
|---|---|---|---|---|---|
| Silica aerogel composites | |||||
| 1 | 134.08 | 47.65 | 1.09 | 30.87 | 0.69 |
| 2 | 266.48 | 92.77 | 0.87 | 71.26 | 0.29 |
| 3 | 117.68 | 32.64 | 0.12 | 13.93 | 2.46 |
| 4 | 173.79 | 49.67 | 0.15 | 33.22 | 0.19 |
| 5 | 120.44 | 39.16 | 0.15 | 17.00 | 0.38 |
| 6 | 102.08 | 28.13 | 0.04 | 11.53 | 2.42 |
| 7 | 120.27 | 52.12 | 0.05 | 35.15 | 0.14 |
| 8 | 82.34 | 40.62 | 0.28 | 21.89 | 0.54 |
| 9 | 77.99 | 28.86 | 0.02 | 11.47 | 2.49 |
| 10 | 121.21 | 60.67 | 0.07 | 35.26 | 0.43 |
| PMMA nanocellular foam | |||||
| 1 | 403.24 | 79.30 | 1.40 | 51.00 | 0.05 |
| Material | Drying a | Bulk Density/ kg/m3 | Pore Volume/ cm3/g | Pore Diameter/ nm | Thermal Conductivity/ mW/(m K) | Reference |
|---|---|---|---|---|---|---|
| Polyamide Pulp-silica aerogel composite | APD | 229 | n.a. | 30.0 | 26.6 | Ghica M.E. et al., 2020 [66] |
| Endothermic opacifier doped silica aerogel | HTSCD | n.a. | n.a. | n.a | 24.6 | Pang H-Q. et al., 2022 [67] |
| ZrO2 b fiber reinforced ZrO2–SiO2 aerogel composite | scCO2 | 230 | n.a. | n.a | 23.6 | Hou X. et al., 2018 [68] |
| Silica fiber-reinforced-silica aerogel | APD | 125 | 7.44 | 39.0 | 22.9 | Torres R.B. et al., 2019 [69] |
| Waterglass silica aerogel | FD | n.a. | 1.92 | 7.7 | 21.5 | Pan Y. et al., 2018 [70] |
| sepiolite/silica aerogel composite | HTSCD | 190 | 3.2 | n.a. | 19.7 | Li X. et al., 2013 [71] |
| Silica aerogel powder | APD | 142 | 2.7 | 12.9 | 19.4 | Zhao S. et al., 2020 [72] |
| Waterglass silica aerogel powder | APD | 110 | 2.72 | 12.9 | 19.4 | Stojanovic A. et al., 2019 [73] |
| TEOS silica aerogel powder | APD | 70 | 3.95 | 17.6 | 18.8 | Stojanovic A. et al., 2019 [73] |
| PI-silica aerogel | APD | 81 | n.a. | n.a. | 18 | Liu R. et al., 2021 [74] |
| Pullulan/PVA-silica aerogel composite | scCO2 | 99 | 2.4 | 60 | 17.7 | Zhao S. et al., 2018 [75] |
| TENCEL® fibers (8 mm at 0.5 vol%) reinforced silica aerogel | scCO2 | 112 | n.a. | n.a. | 15.8 | Jaxel J. et al., 2017 [76] |
| Silica Aerogel Granulate | APD | 131 | 7.1 | 34 | 15 | Huber L. et al., 2017 [77] |
| Vestanat® EP-M 95 reinforced silica aerogel | scCO2 | 106 | 8.7 | 44.2 | 14.7 | Iswar S. et al., 2018 [78] |
| silica aerogel | scCO2 | 115 | 8.2 | 38.5 | 14.5 | Iswar S. et al., 2021 [79] |
| Silica-nanofribillated cellulose composite aerogel | scCO2 | 130 | 1.3 | 46 | 13.8 | Zhao S. et al., 2015 [80] |
| reticulate aerogels from PTMSPMA c | scCO2 | 99 | n.a. | n.a | 10.0 | Rezaei S. et al., 2020 [81] |
| Material | Drying a | Bulk Density/ kg/m3 | Pore Diameter/ nm | Thermal Conductivity/ (mW/(m K)) | Reference |
|---|---|---|---|---|---|
| Poly(Urethane Acrylates) and Poly(Urethane | scCO2 | 140–660 | 1.7–300 | 36–85 | Bang A. et al., 2014 [93] |
| Polyurethane aerogels (using different isocyanates and polyols) | scCO2 | 90–760 | 8.3–31.9 | 31–103 | Chidambareswarapattar C. et al., 2013 [94] |
| Polyurethane aerogels with MDI | scCO2, APD | 200–240 | n.a. | 22–24 | Rigacci A. et al., 2004 [95] |
| PUR-PIR b aerogels | scCO2 | 150–490 | 100–240 | 19–36 | Zhu Z. et al., 2017 [96] |
| Polyurethane aerogels with MDI | scCO2 | 120–230 | 15–210 | 17–24 | Diascorn N. et al., 2015 [97] |
| PIR and PUR-based aerogels | scCO2 | 150–260 | 11.2–17.5 | 15–22 | Biesmans G. et al., 1998 [98] |
| PIR and PUR-based aerogels | scCO2 | 101–165 | 72–721 | 12–24 | Merillas B. et al., 2022 [91] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merillas, B.; Vareda, J.P.; Martín-de León, J.; Rodríguez-Pérez, M.Á.; Durães, L. Thermal Conductivity of Nanoporous Materials: Where Is the Limit? Polymers 2022, 14, 2556. https://doi.org/10.3390/polym14132556
Merillas B, Vareda JP, Martín-de León J, Rodríguez-Pérez MÁ, Durães L. Thermal Conductivity of Nanoporous Materials: Where Is the Limit? Polymers. 2022; 14(13):2556. https://doi.org/10.3390/polym14132556
Chicago/Turabian StyleMerillas, Beatriz, João Pedro Vareda, Judith Martín-de León, Miguel Ángel Rodríguez-Pérez, and Luisa Durães. 2022. "Thermal Conductivity of Nanoporous Materials: Where Is the Limit?" Polymers 14, no. 13: 2556. https://doi.org/10.3390/polym14132556
APA StyleMerillas, B., Vareda, J. P., Martín-de León, J., Rodríguez-Pérez, M. Á., & Durães, L. (2022). Thermal Conductivity of Nanoporous Materials: Where Is the Limit? Polymers, 14(13), 2556. https://doi.org/10.3390/polym14132556