Investigation of Mechanical Behaviors of Functionally Graded CNT-Reinforced Composite Plates
Abstract
:1. Introduction
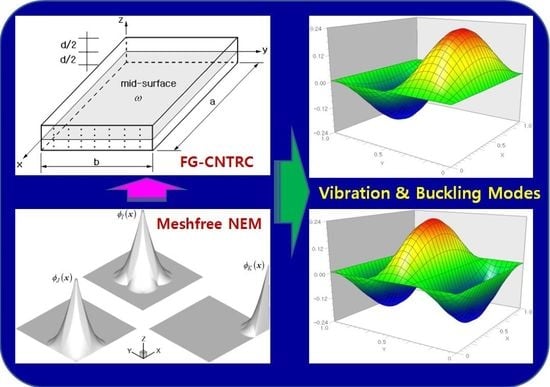
2. Modeling of FG-CNTRC Plates
3. Analysis of Bending, Free-Vibration, and Buckling
4. Results and Discussion
5. Conclusions
- The accuracy of the present method is justified with the peak relative differences between the proposed method and the references, which are 1.01% for the central deflection, 6.07% for the natural frequencies, and 6.12% for the buckling loads.
- The central deflection is significantly reduced by introducing only a small amount of CNTs, and its reduction is proportional to . The natural frequencies and buckling loads show a completely reverse trend.
- The (2,1) and (2,2) modes show higher frequencies than the (1,3) and (1,4) modes because CNTs are parallel to the x-direction. In other words, the stiffness in the x-direction is much higher than that in the y-direction.
- UD, FG-O, and FG-X produce anti-symmetric normal stress distributions and symmetric shear stress distributions; FG-V does not show such distribution but rather a leaning parabolic distribution.
- The buckling load is sensitive to the type of boundary condition, and it increases and saturates in proportion to the aspect ratio. The difference in the buckling load between boundary conditions becomes insensitive in proportion to the aspect ratio.
- The comparison of the magnitudes of the central deflection, fundamental frequency, and buckling load shows that the order of stiffness of the FG-CNTRC plates is FG-X > UD > FG-V > FG-O.
Author Contributions
Funding
Conflicts of Interest
References
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical analysis of functionally graded carbon nanotibe reinforced composite: A review. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Esawi, A.M.K.; Farag, M.M. Carbon nanotube reinforced composites: Potential and current challenges. Mater. Des. 2007, 28, 2394–2401. [Google Scholar] [CrossRef]
- Wang, Z.X.; Shen, H.S. Nonlinear vibration of nanotube-reinforced composite plates in thermal environments. Comput. Mater. Sci. 2011, 50, 2319–2330. [Google Scholar] [CrossRef]
- Ajayan, P.M.; Stephane, O.; Collix, C.; Trauth, D. Aligned carbon nanotube arrays formed by cutting a polymer resin-nanotube composite. Science 1994, 256, 1212–1214. [Google Scholar] [CrossRef]
- Hu, N.; Fugunaga, H.; Lu, C.; Kameyama, M.; Yan, B. Prediction of elastic properties of carbon nanotube reinforced composites. Proc. R. Soc. A 2005, 461, 1685–1710. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanobute composites. Comput. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]
- Wuite, J.; Adali, S. Deflection and stress behavior of nanocomposite reinforced beams using a multiscale amalysis. Compos. Struct. 2005, 71, 388–396. [Google Scholar] [CrossRef]
- Formica, G.; Lacarbonara, W.; Alessi, R. Vibrations of carbon nanotube-reinforced composites. J. Sound Vib. 2010, 329, 1875–1889. [Google Scholar] [CrossRef]
- Arani, A.; Maghamikia, S.; Mohammadimehr, M.; Arefmanesh, A. Buckling analysis of laminated composite rectangular plates reinforced by SWCNTS using analytical and finite element methods. J. Mech. Sci. Technol. 2011, 25, 809–820. [Google Scholar] [CrossRef]
- Seidel, G.D.; Lagoudas, D.C. Micromechanical analysis of the effective elastic properties of carbon nanotube reinforced composites. Mech. Mater. 2006, 38, 884–907. [Google Scholar] [CrossRef]
- Qian, S.; Dickey, E.C.; Andrews, R.; Rantell, T. Load transfer and deformation mechanism in carbon nanotube-polystyrene composites. Appl. Phys. Lett. 2000, 76, 2868. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.R.; Oden, J.T. Functionally graded material: A parametric study on thermal-stress characteristics using the Crank-Nicolson-Galerkin scheme. Comput. Methods Appl. Mech. Eng. 2000, 188, 17–38. [Google Scholar] [CrossRef]
- Smaranda, I.; Nila, A.; Ganea, P.; Daescu, M.; Zgura, I.; Ciobanu, R.C.; Trandabat, A.; Baibarac, M. The influence of the ceramic nanoparticles on the thermoplastic polymers matrix: Their structural, optical, and conductive properties. Polymers 2021, 13, 2773. [Google Scholar] [CrossRef]
- Shen, S.H. Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos. Struct. 2009, 19, 9–19. [Google Scholar] [CrossRef]
- Ke, L.L.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of functionally graded carbon nanotube-reinforced composite beams. Compos. Struct. 2010, 92, 676–683. [Google Scholar] [CrossRef]
- Ray, M.C.; Batra, R.C. A single-walled carbon nanotube reinforced 1-3 piezoelectric composite for active control of smart structures. Smart Mater. Struct. 2009, 19, 1936. [Google Scholar] [CrossRef]
- Van Do, V.N.; Lee, C.H. Bending analyses of FG-CNTRC plates using the modified mesh-free radial point interpolation method based on the higher-order shear deformation theory. Compos. Struct. 2017, 168, 485–497. [Google Scholar]
- Mirzaei, M.; Kiani, Y. Nonlinear free vibration of FG-CNT reinforced composite plates. Struct. Eng. Mech. 2017, 64, 381–390. [Google Scholar]
- Kelesthteri, M.M.; Asadi, H.; Aghdam, M.M. Nonlinear bending analysis of FG-CNTRC annular plates with variable thickness on elastic foundation. Thin-Wall Struct. 2019, 135, 453–462. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.X.; Liew, K.M. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
- Civalek, Ö.; Avcar, M. Free vibration and buckling analyses of CNT reinforced laminated non-rectangular plates by discrete singular convolution method. Eng. Comput. 2020, 38, 489–521. [Google Scholar] [CrossRef]
- Arefi, M.; Firouzeh, S.; Bidgoli, E.M.R.; Civalek, Ö. Analysis of porous micro-plates reinforced with FG-GNPs based on Reddy plate theory. Compos. Struct. 2020, 247, 112391. [Google Scholar] [CrossRef]
- Gopalan, V.; Suthenthiraveerappa, V.; Annamalai, A.R.; Manivannan, S.; Pragasam, V.; Chinnaiyan, A.R.; Mannayee, G.; Jen, C.P. Dynamic characteristics of woven flax/epoxy laminated composite plate. Polymers 2021, 13, 209. [Google Scholar] [CrossRef] [PubMed]
- Cheshmeh, E.; Karbon, M.; Eyvazian, A.; Jung, D.W.; Habibi, M.; Safarpour, M. Buckling and vibration analysis of FG-CNTRC plate subjected to thermo-mechanical load based on higher order shear deformation theory. Mech. Based Des. Struct. Mech. 2020, 50, 1137–1160. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Daikh, A.A.; Eltaher, M.A. Novel quasi 3D theory for mechanical responses of FG-CNTs reinforced composite nanoplates. Adv. Nano Res. 2022, 12, 117–137. [Google Scholar]
- Cho, J.R. Natural element approximation of hierarchical models of plate-like elastic structures. Finite Elem. Anal. Des. 2020, 180, 103439. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, H.W. A Petrov-Galerkin natural element method securing the numerical integration accuracy. J. Mech. Sci. Technol. 2006, 20, 94–109. [Google Scholar] [CrossRef]
- Wong, M.; Paramsothy, M.; Xu, X.J.; Ren, Y.; Li, S.; Liao, K. Physical interactions at carbon-nanotube-polymer interface. Polymer 2003, 44, 7757–7764. [Google Scholar] [CrossRef]
- Sukumar, N.; Moran, B.; Belytschko, T. The natural element method in solid mechanics. Int. J. Numer. Methods Eng. 1998, 43, 839–887. [Google Scholar] [CrossRef]
- Chinesta, F.; Cescotto, C.; Cueto, E.; Lorong, P. Natural Element Method for the Simulation of Structures and Processes; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates: Theory and Analysis; CRC Press: New York, NY, USA, 1997. [Google Scholar]
- Adam, C.; Bouabdallah, C.; Zarroug, M.; Maitourrnam, H. Improved numerical integration for locking treatment in isogemetric structural elements. Part II: Plates and shells. Comput. Meth. Appl. Mech. Eng. 2015, 284, 106–137. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Too, J.M. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971, 3, 275–290. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, H.W. Polygon-wise constant curvature natural element approximation of Kirchhoff plate model. Int. J. Solids Struct. 2007, 44, 4860–4871. [Google Scholar] [CrossRef] [Green Version]








| 0.11 | 0.149 | 0.934 | 0.934 |
| 0.14 | 0.150 | 0.941 | 0.941 |
| 0.17 | 0.149 | 1.381 | 1.381 |
| CNTRC | |||||||
|---|---|---|---|---|---|---|---|
| 10 | 20 | 50 | |||||
| Present | Ref. [20] | Present | Ref. [20] | Present | Ref. [20] | ||
| 0.11 | UD | 3.768 × 10−3 | 3.739 × 10−3 | 3.639 × 10−2 | 3.628 × 10−2 | 1.155 | 1.155 |
| FG-V | 4.481 × 10−3 | 4.466 × 10−3 | 4.905 × 10−2 | 4.879 × 10−2 | 1.658 | 1.653 | |
| FG-O | 5.223 × 10−3 | 5.230 × 10−3 | 6.192 × 10−2 | 6.155 × 10−2 | 2.153 | 2.157 | |
| FG-X | 3.209 × 10−3 | 3.177 × 10−3 | 2.735 × 10−2 | 2.701 × 10−2 | 0.794 | 0.790 | |
| 0.14 | UD | 3.329 × 10−3 | 3.306 × 10−3 | 3.017 × 10−2 | 3.001 × 10−2 | 0.935 | 0.918 |
| FG-V | 3.906 × 10−3 | 3.894 × 10−3 | 4.068 × 10−2 | 4.025 × 10−2 | 1.356 | 1.326 | |
| FG-O | 4.521 × 10−3 | 4.525 × 10−3 | 5.146 × 10−2 | 5.070 × 10−2 | 1.771 | 1.738 | |
| FG-X | 2.86 × 10−3 | 2.844 × 10−3 | 2.285 × 10−2 | 2.256 × 10−2 | 0.639 | 0.627 | |
| 0.17 | UD | 2.413 × 10−3 | 2.394 × 10−3 | 2.354 × 10−2 | 2.348 × 10−2 | 0.750 | 0.752 |
| FG-V | 2.875 × 10−3 | 2.864 × 10−3 | 3.185 × 10−2 | 3.174 × 10−2 | 1.080 | 1.082 | |
| FG-O | 3.37 × 10−3 | 3.378 × 10−3 | 4.038 × 10−2 | 4.020 × 10−2 | 1.407 | 1.416 | |
| FG-X | 2.032 × 10−3 | 2.012 × 10−3 | 1.756 × 10−2 | 1.737 × 10−2 | 0.513 | 0.513 | |
| Mode (m,n) | UD | FG-V | FG-O | FG-X | |||||
|---|---|---|---|---|---|---|---|---|---|
| Present | Ref. [20] | Present | Ref. [20] | Present | Ref. [20] | Present | Ref. [20] | ||
| 0.11 | (1,1) | 19.265 | 19.223 | 16.323 | 16.252 | 14.427 | 14.302 | 22.923 | 22.984 |
| (1,2) | 23.859 | 23.408 | 21.717 | 21.142 | 20.058 | 19.373 | 26.847 | 26.784 | |
| (1,3) | 36.131 | 34.669 | 34.715 | 33.350 | 33.027 | 31.615 | 38.406 | 37.591 | |
| (1,4) | 56.365 | 54.043 | 54.075 | 53.430 | 52.990 | 51.370 | 58.430 | 56.946 | |
| (2,1) | 72.560 | 70.811 | 63.844 | 60.188 | 54.111 | 53.035 | 85.007 | 83.150 | |
| (2,2) | 74.799 | 72.900 | 64.256 | 62.780 | 57.185 | 55.823 | 86.811 | 84.896 | |
| 0.14 | (1,1) | 21.394 | 21.354 | 18.053 | 17.995 | 15.912 | 15.801 | 25.495 | 25.555 |
| (1,2) | 25.607 | 25.295 | 23.102 | 22.643 | 21.157 | 20.563 | 29.094 | 29.192 | |
| (1,3) | 37.525 | 36.276 | 35.839 | 34.660 | 33.843 | 32.509 | 40.344 | 39.833 | |
| (1,4) | 57.741 | 55.608 | 56.444 | 54.833 | 53.821 | 52.184 | 60.439 | 59.333 | |
| (2,1) | 80.100 | 78.110 | 67.859 | 66.552 | 59.805 | 58.748 | 89.442 | 87.814 | |
| (2,2) | 82.079 | 80.015 | 70.429 | 68.940 | 62.573 | 61.277 | 93.039 | 91.299 | |
| 0.17 | (1,1) | 23.743 | 23.697 | 20.074 | 19.982 | 17.708 | 17.544 | 28.326 | 28.413 |
| (1,2) | 29.523 | 28.987 | 26.914 | 26.204 | 24.665 | 23.783 | 33.455 | 33.434 | |
| (1,3) | 44.881 | 43.165 | 43.269 | 41.646 | 40.674 | 38.855 | 48.301 | 47.547 | |
| (1,4) | 70.129 | 67.475 | 68.922 | 66.943 | 65.351 | 63.179 | 73.793 | 72.570 | |
| (2,1) | 89.534 | 87.385 | 75.563 | 74.030 | 66.489 | 65.154 | 105.213 | 102.939 | |
| (2,2) | 92.360 | 90.031 | 79.191 | 77.343 | 70.311 | 68.579 | 107.597 | 105.334 | |
| Load | Method | UD | FG-O | FG-X | |
|---|---|---|---|---|---|
| Uniaxial | 0.11 | Ref. [28] | 39.2456 | 21.4573 | 56.7512 |
| Present | 39.4211 | 21.6428 | 56.9679 | ||
| 0.14 | Ref. [28] | 49.2112 | 26.3671 | 71.8512 | |
| Present | 49.6621 | 26.9072 | 72.1240 | ||
| 0.17 | Ref. [28] | 59.5136 | 31.2315 | 87.8012 | |
| Present | 60.8003 | 33.1455 | 88.3366 | ||
| Biaxial | 0.11 | Ref. [28] | 11.1118 | 7.4945 | 14.2417 |
| Present | 11.2592 | 7.6119 | 14.4603 | ||
| 0.14 | Ref. [28] | 13.1545 | 8.3545 | 16.2198 | |
| Present | 13.4774 | 8.8108 | 17.6572 | ||
| 0.17 | Ref. [28] | 17.2852 | 11.2654 | 22.8545 | |
| Present | 17.5464 | 11.7204 | 22.9129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.-R.; Ahn, Y.-J. Investigation of Mechanical Behaviors of Functionally Graded CNT-Reinforced Composite Plates. Polymers 2022, 14, 2664. https://doi.org/10.3390/polym14132664
Cho J-R, Ahn Y-J. Investigation of Mechanical Behaviors of Functionally Graded CNT-Reinforced Composite Plates. Polymers. 2022; 14(13):2664. https://doi.org/10.3390/polym14132664
Chicago/Turabian StyleCho, Jin-Rae, and Young-Ju Ahn. 2022. "Investigation of Mechanical Behaviors of Functionally Graded CNT-Reinforced Composite Plates" Polymers 14, no. 13: 2664. https://doi.org/10.3390/polym14132664
APA StyleCho, J. -R., & Ahn, Y. -J. (2022). Investigation of Mechanical Behaviors of Functionally Graded CNT-Reinforced Composite Plates. Polymers, 14(13), 2664. https://doi.org/10.3390/polym14132664