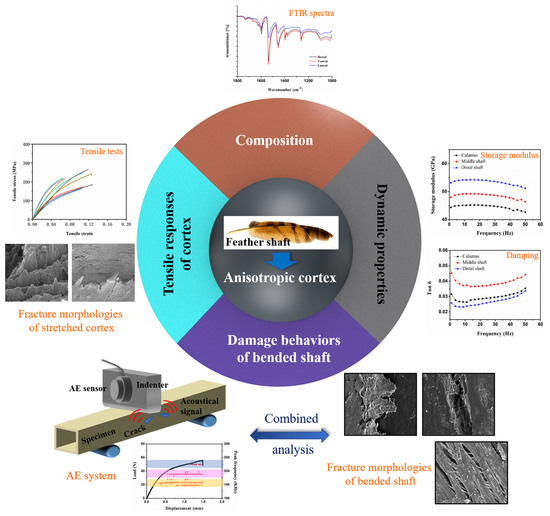
Anisotropic Composition and Mechanical Behavior of a Natural Thin-Walled Composite: Eagle Feather Shaft
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Analysis for Protein Composition of Cortex
2.3. Tensile Testing
2.4. Dynamic Mechanical Testing
2.5. Characterizations of Flexural Properties and Fracture Behaviors
3. Results and Discussion
3.1. Protein Composition of the Feather Shafts
3.2. Tensile Response
3.3. Frequency Scans by DMA
3.4. Damage Behaviors of Bended Feather Shaft
4. Conclusions
- The keratin composition of the calamus cortex is almost homogeneous. In rachis, both the HBs and the side-chain in the lateral cortex are less than that in the dorsal cortex and ventral cortex. Besides, the HBs and side-chain in the dorsal cortex of the middle shaft are much higher than that in other segments.
- The tensile properties, including Young’s modulus, tensile strength and breaking strain, are influenced by the keratin structure and fibrous structure. The dominant damage pattern of the stretched dorsal cortex varies from transverse fracture with fiber rupture to axial splitting towards the distal side of the shaft due to the gradual reduction of the circumferential fibers. The lateral cortex of rachis exhibits zigzag fracture with extensive delamination due to the crossed fibrous structure.
- The varied trend of the storage modulus of cortex strips is consistent with Young’s modulus. The storage modulus of the dorsal cortex on the distal shaft is the highest, and the lateral cortex shows lower storage modulus than other parts, which result from the different keratin composition and fibrous structure. The damping of dorsal and ventral cortex on distal shaft is relatively superior due to the larger amount of side chains and the interface motion between axial fiber and matrix.
- The shafts under bending load fail due to the fracture of dorsal cortex on compressive side. The matrix breakage and fiber dissociation firstly occur in calamus and then deteriorate; finally, the calamus fails due to the fiber rupture. Many ‘ligament-like’ fiber bundles can be observed on bended middle shaft, which are caused by initial matrix breakage and subsequent crack deflection by fiber. The distal shaft is broken by persistent matrix fracture with few fibers’ dissociation and rupture, leading to a smooth crack edge. Moreover, both in the middle and distal shafts, discontinuous microcracks are spawned on the lateral cortex and constrained by crossed fiber.
- Further study to design and fabricate a novel thin-walled structure, which is stimulated by findings and analyses, including the anisotropic features and damage behaviors of flight feather shaft in this work, is anticipated to be carried out in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Q.; Mo, Z.; Wu, Y.; Ma, J.; Tsui, G.C.P.; Hui, D. Crush response of CFRP square tube filled with aluminum honeycomb. Compos. Pt. B-Eng. 2016, 98, 406–414. [Google Scholar] [CrossRef]
- Liu, Q.; Ou, Z.; Mo, Z.; Li, Q.; Qu, D. Experimental investigation into dynamic axial impact responses of double hat shaped CFRP tubes. Compos. Pt. B-Eng. 2015, 79, 494–504. [Google Scholar] [CrossRef]
- Liu, T.; Hou, S.; Nguyen, X.; Han, X. Energy absorption characteristics of sandwich structures with composite sheets and bio coconut core. Compos. Pt. B-Eng. 2017, 114, 328–338. [Google Scholar] [CrossRef]
- Kathiresan, M.; Manisekar, K. Axial crush behaviours and energy absorption characteristics of aluminium and E-glass/epoxy over-wrapped aluminium conical frusta under low velocity impact loading. Compos. Struct. 2016, 136, 86–100. [Google Scholar] [CrossRef]
- Xiao, Y.; Hu, Y.; Zhang, J.; Song, C.; Liu, Z.; Yu, J. Dynamic bending responses of CFRP thin-walled square beams filled with aluminum honeycomb. Thin-Walled Struct. 2018, 132, 494–503. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Jiao, D.; Meyers, M.A.; Zhang, Z.F. Structure and mechanical properties of naturally occurring lightweight foam-filled cylinder-the peacock’s tail coverts shaft and its components. Acta Biomater. 2015, 17, 137–151. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chen, P.Y.; Lopez, M.I.; Seki, Y.; Lin, A. Biological materials: A materials science approach. J. Mech. Behav. Biomed. Mater. 2011, 4, 626–657. [Google Scholar] [CrossRef]
- Wang, B.; Sullivan, T.N. A review of terrestrial, aerial and aquatic keratins: The structure and mechanical properties of pangolin scales, feather shafts and baleen plates. J. Mech. Behav. Biomed. Mater. 2017, 76, 4–20. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, Z.; Guo, E.; Kong, X.; Kang, H.; Xu, Y.; Li, R.; Fan, G.; Wang, T. Micro hierarchical structure and mechanical property of Sparrow Hawk (accipiter nisus) feather shaft. CMES-Comp. Model. Eng. Sci. 2021, 127, 705–720. [Google Scholar]
- Wang, B.; Meyers, M.A. Light like a feather: A fibrous natural composite with a shape changing from round to square. Adv. Sci. 2016, 4, 1600360. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Meyers, M.A. Seagull feather shaft: Correlation between structure and mechanical response. Acta Biomater. 2017, 48, 270–288. [Google Scholar] [CrossRef] [PubMed]
- Astbury, W.T.; Marwick, T.C. X-ray interpretation of the molecular structure of feather keratin. Nature 1932, 130, 309–310. [Google Scholar] [CrossRef]
- Fraser, R.; Macrae, T.P.; Rogers, G. Keratins: Their composition, structure, and biosynthesis. Q. Rev. Biol. 1972, 845, 304. [Google Scholar]
- Fraser, R.; Parry, D. The molecular structure of reptilian keratin. Int. J. Biol. Macromol. 1996, 19, 207–211. [Google Scholar] [CrossRef]
- Fraser, R.; Parry, D. Molecular packing in the feather keratin filament. J. Struct. Biol. 2008, 162, 1–13. [Google Scholar] [CrossRef]
- Fraser, R.; Parry, D. The structural basis of the filament-matrix texture in the avian/reptilian group of hard β-keratins. J. Struct. Biol. 2011, 173, 391–405. [Google Scholar] [CrossRef]
- Yang, W.; Mckittrick, J.; Meyers, M.A. Keratin: Structure, mechanical properties, occurrence in biological organisms, and efforts at bioinspiration. Prog. Mater. Sci. 2016, 76, 229–318. [Google Scholar]
- Theagarten, L.S.; Nelisha, M.; Daniel, O. A new helical crossed-fibre structure of β-keratin in flight feathers and its biomechanical implications. PLoS ONE 2013, 8, e65849. [Google Scholar]
- Zou, M.; Xu, L.; Zhou, J.; Song, J.; Liu, S.; Li, X. Microstructure and compression resistance of bean goose (Anser fabalis) feather shaft. Microsc. Res. Tech. 2020, 83, 156–164. [Google Scholar] [CrossRef]
- Ide, N.; Yamashita, M.; Asano, S. Solid solution hardening evaluated from amplitude-dependent internal friction in polycrystalline copper alloys. Scr. Mater. 1999, 41, 181–185. [Google Scholar] [CrossRef]
- Ouytsel, K.V.; Batist, R.D.; Schaller, R. Dislocation-defect interactions in nuclear reactor pressure-vessel steels investigated by means of internal friction. J. Alloy. Compd. 2000, 310, 445–448. [Google Scholar] [CrossRef]
- Jia, Y.; Li, K.; Xue, L.; Ren, J.; Zhang, S. Internal friction behaviour of carbon fibre reinforced multilayered (PyC–SiC)n matrix composites. Compos. Pt. B-Eng. 2017, 114, 8–14. [Google Scholar] [CrossRef]
- Yang, C.; Wu, J.; Ditta, A.; Wu, S.; Zhao, Z. Influence of high-temperature oxidation and test conditions on the dynamic mechanical properties of 2.5D SiCf/SiCm composites. Materials 2020, 14, 145. [Google Scholar] [CrossRef]
- Weiss, I.M.; Kirchner, H. The peacock’s train (Pavo cristatus and Pavo cristatus mut. alba) I. structure, mechanics, and chemistry of the tail feather coverts. J. Exp. Zool. Part. A. 2010, 313a. [Google Scholar] [CrossRef]
- Purslow, P.; Vincent, J. Mechanical properties of primary feathers from the pigeon. J. Exp. Biol. 1978, 72, 251–260. [Google Scholar] [CrossRef]
- Macleod, G. Mechanical properties of contour feathers. J. Exp. Biol. 1980, 87, 65–72. [Google Scholar] [CrossRef]
- Worcester, S.E. The scaling of the size and stiffness of primary flight feathers. Proc. Zool. Soc. Lond. 2010, 239, 609–624. [Google Scholar] [CrossRef]
- Bachmann, T.; Emmerlich, J.; Baumgartner, W.; Schneider, J.M.; Wagner, H. Flexural stiffness of feather shafts: Geometry rules over material properties. J. Exp. Biol. 2012, 215, 405–415. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crenshaw, D.G. Design and materials of feather shafts: Very light, rigid structures. J. Biomech. 1980, 13, 199. [Google Scholar] [CrossRef]
- Corning, W.R.; Biewener, A.A. In vivo strains in pigeon flight feather shafts: Implications for structural design. J. Exp. Biol. 1998, 201, 3057–3065. [Google Scholar] [CrossRef]
- Rosa, I.; Santulli, C.; Sarasini, F. Acoustic emission for monitoring the mechanical behaviour of natural fibre composites: A literature review. Compos. Pt. A-Appl. Sci. Manuf. 2009, 40, 1456–1469. [Google Scholar] [CrossRef]
- Gutkin, R.; Green, C.J.; Vangrattanachai, S.; Pinho, S.T.; Robinson, P.; Curtis, P.T. On acoustic emission for failure investigation in CFRP: Pattern recognition and peak frequency analyses. Mech. Syst. Signal. Proc. 2011, 25, 1393–1407. [Google Scholar] [CrossRef]
- Zhao, D.; Mao, K.; Yang, Y.; Hamada, H. Flexural behavior evaluation of needle-punched glass/jute hybrid mat reinforced polymer composites. Procedia Eng. 2017, 200, 10–17. [Google Scholar] [CrossRef]
- Tian, W.; Yang, K.; Wu, S.; Yang, J.; Ritchie, R.O. Impact of hydration on the mechanical properties and damage mechanisms of natural silk fibre reinforced composites. Compos. Pt. A-Appl. Sci. Manuf. 2021, 147, 106458. [Google Scholar] [CrossRef]
- Takahashi, K.; Yamamoto, H.; Yokote, Y.; Hattori, M. Thermal behavior of fowl feather keratin. Biosci. Biotechnol. Biochem. 2004, 68, 1875–1881. [Google Scholar] [CrossRef] [Green Version]
- Martin, P.A.; Bradford, G.D.; Gous, R.M. A formal method of determining the dietary amino acid requirements of laying-type pullets during their growing period. Br. Poult. Sci. 1994, 35, 709–724. [Google Scholar] [CrossRef]
- Astm, D. Standard test method for tensile properties of polymer matrix composite materials. Astm 2008, 1–6. [Google Scholar]
- Specimens, P.; Materials, E.I. Standard test methods for flexural properties of unreinforced and reinforced plastics and electrical insulating materials. Astm 2010, 1–11. [Google Scholar]
- Cardamone, J.M. Investigating the microstructure of keratin extracted from wool: Peptide sequence (MALDI-TOF/TOF) and protein conformation (FTIR). J. Mol. Struct. 2010, 969, 97–105. [Google Scholar] [CrossRef]
- Ha, S.W. Structural study of bombyx mori silk fibroin during processing for regeneration. Diss. Abstr. Int. 2005, 3162442. [Google Scholar]
- Aluigi, A.; Zoccola, M.; Vineis, C.; Tonin, C.; Ferrero, F.; Canetti, M. Study on the structure and properties of wool keratin regenerated from formic acid. Int. J. Biol. Macromol. 2007, 41, 266–273. [Google Scholar] [CrossRef]
- Garidel, P.; Schott, H. Fourier-transform midinfrared spectroscopy for analysis and screening of liquid protein formulations. Part 2: Detailed analysis and applications. BioProcess Int. 2006, 48–55. [Google Scholar]
- Bandekar, J. Amide modes and protein conformation. Biochim. Biophys. Acta Protein Struct. Mol. Enzymol. 1992, 1120, 123–143. [Google Scholar] [CrossRef]
- Krimm, S.; Bandekar, J. Vibrational spectroscopy and conformation of peptides, polypeptides, and proteins. Adv. Protein Chem. 1986, 38, 181–364. [Google Scholar]
- Huang, W.; Zaheri, A.; Yang, W.; Kisailus, D.; Ritchie, R.O.; Espinosa, H.; Mckittrick, J. How water can affect keratin: Hydration-driven recovery of bighorn sheep (Ovis Canadensis) horns. Adv. Funct. Mater. 2019, 29, 1901077. [Google Scholar] [CrossRef]
- Wang, H.N.; Yang, M.X.; Luo, L.B.; Huang, J.Y.; Li, K.; Xu, W.; Yan, F. Catalysis and inhibition of benzimidazole units on thermal imidization of poly (amic acid) via hydrogen bonding interactions. Chin. J. Polym. Sci. 2015, 12, 621–632. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Q. Synthesis and properties of polyimides derived from diamine monomer containing bi-benzimidazole unit. J. Polym. Res. 2014, 21, 424. [Google Scholar] [CrossRef]
- Chung, I.S.; Hong, K.; Chan, E.P.; Sang, Y.K. Soluble polyimides from unsymmetrical diamine containing benzimidazole ring and trifluoromethyl pendent group. Polymer 2008, 49, 2644–2649. [Google Scholar]
- Zhang, P.; Chen, Y.; Li, G.; Luo, L.; Pang, Y.; Wang, X.; Peng, C.; Liu, X. Enhancement of properties of polyimide/silica hybrid nanocomposites by benzimidazole formed hydrogen bond. Polym. Adv. Technol. 2012, 23, 1362–1368. [Google Scholar] [CrossRef]
- Fradkin, D.G.; Foster, J.N.; Sperling, L.H.; Thomas, D.A. A quantitative determination of the damping behavior of acrylic based interpenetrating polymer networks. Rubber Chem. Technol. 1986, 59, 255–262. [Google Scholar] [CrossRef]
- Chang, M.C.O.; Thomas, D.A.; Sperling, L.H. Characterization of the area under loss modulus and tanδ-temperature curves: Acrylic polymers and their sequential interpenetrating polymer networks. J. Appl. Polym. Sci. 2010, 34, 409–422. [Google Scholar] [CrossRef]
- Fay, J.J.; Thomas, D.A.; Sperling, L.H. Evaluation of the area under linear loss modulus-temperature curves. J. Appl. Polym. Sci. 2010, 43, 1617–1623. [Google Scholar] [CrossRef]
- Riyanto; Yusmiati; Cahyandaru, N. Isolation and characterization of keratin from chicken feathers. AIP Conf. Proc. 2020, 2229, 030038. [Google Scholar]
- Earland, C.; Blakey, P.R.; Stell, J. Studies on the structure of keratin IV. The molecular structure of some morphological components of keratins. Biochim. Biophys. Acta 1962, 56, 268–274. [Google Scholar] [CrossRef]
- Earland, C.; Blakey, P.R.; Stell, J.G.P. Molecular orientation of some keratins. Nature 1962, 196, 1287–1291. [Google Scholar] [CrossRef]
- Cameron, G.J.; Wess, T.J.; Bonser, R. Young’s modulus varies with differential orientation of keratin in feathers. J. Struct. Biol. 2003, 143, 118–123. [Google Scholar] [CrossRef]
- Menard, K.P. Dynamic Mechanical Analysis: A Practical Introduction. Biopolymers 1999. [Google Scholar]
- Matthews, F.L. Stress Analysis of Fiber-Reinforced Composite Materials; McGraw-Hill Companies, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Chen, G.; Luo, H.; Yang, H.; Zhang, T.; Li, S. Water effects on the deformation and fracture behaviors of the multi-scaled cellular fibrous bamboo. Acta Biomater. 2018, 65, 203–215. [Google Scholar] [CrossRef]
- Ramirez-Jimenez, C.; Papadakis, N.; Reynolds, N.; Gan, T.; Purnell, P.; Pharaoh, M. Identification of failure modes in glass/polypropylene composites by means of the primary frequency content of the acoustic emission event. Compos. Sci. Technol. 2004, 64, 1819–1827. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, S.; Han, B.; Xu, Y.; Guo, E.; Sun, B.; Zeng, Y.; Hou, H.; Wu, S. Anisotropic Composition and Mechanical Behavior of a Natural Thin-Walled Composite: Eagle Feather Shaft. Polymers 2022, 14, 309. https://doi.org/10.3390/polym14020309
Cai S, Han B, Xu Y, Guo E, Sun B, Zeng Y, Hou H, Wu S. Anisotropic Composition and Mechanical Behavior of a Natural Thin-Walled Composite: Eagle Feather Shaft. Polymers. 2022; 14(2):309. https://doi.org/10.3390/polym14020309
Chicago/Turabian StyleCai, Siyu, Baoshuai Han, Yanjin Xu, Enyu Guo, Bin Sun, Yuansong Zeng, Hongliang Hou, and Sujun Wu. 2022. "Anisotropic Composition and Mechanical Behavior of a Natural Thin-Walled Composite: Eagle Feather Shaft" Polymers 14, no. 2: 309. https://doi.org/10.3390/polym14020309
APA StyleCai, S., Han, B., Xu, Y., Guo, E., Sun, B., Zeng, Y., Hou, H., & Wu, S. (2022). Anisotropic Composition and Mechanical Behavior of a Natural Thin-Walled Composite: Eagle Feather Shaft. Polymers, 14(2), 309. https://doi.org/10.3390/polym14020309