Multi-Criteria Evaluation of the Failure of CFRP Laminates for Frames in the Automotive Industry
Abstract
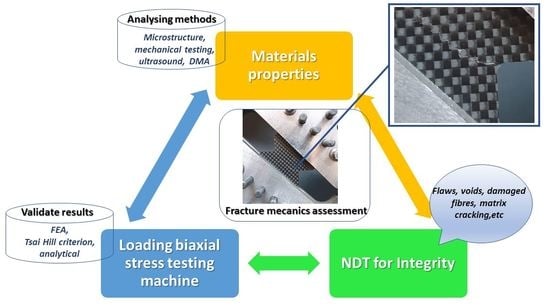
:1. Introduction
2. Materials and Methods
2.1. Materials and Samples
2.2. Finite Element Analysis (FEA)
2.3. Fixture Test
3. Results and Discussions
3.1. Experimental Results
3.1.1. Ultrasound Evaluation
3.1.2. DMA Analyses
3.2. Failure Mechanism Criteria
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guadagno, L.; Sorrentino, A.; Delprat, P.; Vertuccio, L. Design of multifunctional composites: New strategy to save energy and improve mechanical performance. Nanomaterials 2020, 10, 2285. [Google Scholar] [CrossRef]
- Regulation, E.U. No 443/2009 of the European Parliament and of the Council of 23 April 2009 setting emission performance standards for new passenger cars as part of the Community’s integrated approach to reduce CO2 emissions from light-duty vehicles. J. Eur. Union 2009, 140, 5–6. [Google Scholar]
- Ozkan, D.; Gok, M.S.; Karaoglanli, A.C. Carbon fiber reinforced polymer (CFRP) composite materials, their characteristic properties, industrial application areas and their machinability. In Engineering Design Applications III; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany, 2020; pp. 235–253. [Google Scholar] [CrossRef]
- Mathes, V. The composites industry: Plenty of opportunities in a heterogeneous market. Reinforced Plast. 2018, 62, 44–51. [Google Scholar] [CrossRef]
- Zorko, D.; Tavčar, J.; Bizjak, M.; Šturm, R.; Bergant, Z. High cycle fatigue behavior of autoclave-cured woven carbon fiber-reinforced polymer composite gears. Polym. Test. 2021, 102, 107339. [Google Scholar] [CrossRef]
- Othman, R.; Ismail, N.I.; Pahmi, M.A.A.H.; Basri, M.H.M.; Sharudin, H.; Hemdi, A.R. Application of Carbon fiber reinforced plastics in automotive industry: A review. J. Mech. Manuf. 2018, 1, 144–154. [Google Scholar] [CrossRef]
- Petrakli, F.; Gkika, A.; Bonou, A.; Karayannis, P.; Koumoulos, E.P.; Semitekolos, D.; Trompeta, A.F.; Rocha, N.; Santos, R.M.; Simmonds, G.; et al. End-of-Life recycling options of (nano) enhanced CFRP composite prototypes waste—A life cycle perspective. Polymers 2020, 12, 2129. [Google Scholar] [CrossRef] [PubMed]
- Kaw, A.K. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Sang, L.; Wang, Y.; Wang, C.; Peng, X.; Hou, W.; Tong, L. Moisture diffusion and damage characteristics of carbon fabric reinforced polyamide 6 laminates under hydrothermal aging. Compos. Part A-Appl. Sci. 2019, 123, 242–252. [Google Scholar] [CrossRef]
- Alessi, S.; Pitarresi, G.; Spadaro, G. Effect of hydrothermal ageing on the thermal and delamination fracture behaviour of CFRP composites. Compos. Part B-Eng. 2014, 67, 145–153. [Google Scholar] [CrossRef]
- Hübner, M.; Lepke, D.; Hardi, E.; Koerdt, M.; Herrmann, A.S.; Lang, W. Online Monitoring of Moisture Diffusion in Carbon Fiber Composites Using Miniaturized Flexible Material Integrated Sensors. Sensors 2019, 19, 1748. [Google Scholar] [CrossRef] [Green Version]
- Lei, Y.; Kang, Z.; Zhang, J.; Sun, Y.; Zhang, B. Effect of freeze-thaw cycling on the mechanical properties of continuous carbon fiber-reinforced polyamide 6 composites. Polymer Test. 2022, 114, 107704. [Google Scholar] [CrossRef]
- Gao, X.; Yuan, L.; Fu, Y.; Yao, X.; Yang, H. Prediction of mechanical properties on 3D braided composites with void defects. Compos. Part B-Eng. 2020, 197, 108164. [Google Scholar] [CrossRef]
- Zhu, H.; Li, D.S.; Jiang, L. Mesoscale progressive damage and strength analysis of three-dimensional braided composites under tension. Eng. Fract. Mech. 2020, 237, 107221. [Google Scholar] [CrossRef]
- Sadighi, M.; Alderliesten, R. Impact fatigue, multiple and repeated low-velocity impacts on FRP composites: A review. Compos. Struct. 2022, 297, 115962. [Google Scholar] [CrossRef]
- Garnier, C.; Pastor, M.L.; Lorrain, B.; Pantalé, O. Fatigue behavior of impacted composite structures. Compos. Struct. 2013, 100, 443–450. [Google Scholar] [CrossRef] [Green Version]
- Stanciu, M.D.; Drăghicescu, H.T.; Roșca, I.C. Mechanical Properties of GFRPs Exposed to Tensile, Compression and Tensile–Tensile Cyclic Tests. Polymers 2021, 13, 898. [Google Scholar] [CrossRef]
- Junyan, L.; Yang, L.; Fei, W.; Yang, W. Study on probability of detection (POD) determination using lock-in thermography for nondestructive inspection (NDI) of CFRP composite materials. Infrared Phys. Technol. 2015, 71, 448–456. [Google Scholar] [CrossRef]
- de Winton, H.C.; Cegla, F.; Hooper, P.A. A method for objectively evaluating the defect detection performance of in-situ monitoring systems. Addit. Manuf. 2021, 48, 102431. [Google Scholar] [CrossRef]
- Li, C.; He, W.; Nie, X.; Wei, X.; Guo, H.; Wu, X.; Xu, H.; Zhang, T.; Liu, X. Intelligent damage recognition of composite materials based on deep learning and ultrasonic testing. AIP Adv. 2021, 11, 125227. [Google Scholar] [CrossRef]
- Fu, Y.; Yao, X. A review on manufacturing defects and their detection of fiber reinforced resin matrix composites. Compos. Part C Open Access 2022, 8, 100276. [Google Scholar] [CrossRef]
- Tsai, S.W. Strength Characteristics of Composite Materials; Philco Corp: Newport Beach, CA, USA, 1965. [Google Scholar]
- Hoffman, O. The brittle strength of orthotropic materials. J. Compos. Mater. 1967, 1, 200–206. [Google Scholar] [CrossRef]
- Chamis, C. Failure Criteria for Filamentary Composites; Technical Note NASA TN D-5367; National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]
- De Luca, A.; Caputo, F. A review on analytical failure criteria for composite materials. AIMS Mater. Sci. 2017, 4, 1165–1185. [Google Scholar] [CrossRef]
- Lahrech, A.C.; Naidjate, M.; Helifa, B.; Zaoui, A.; Abdelhadi, B.; Lefkaier, I.K.; Feliachi, M. Development of an axial rotating magnetic field multi-coil eddy current sensor for electromagnetic characterization of stratified CFRP materials. NDT E Int. 2022, 126, 102589. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Zhou, F.; Zhang, J.; Song, S.; Yang, D.; Wang, C. Effect of temperature on material properties of carbon fiber reinforced polymer (CFRP) tendons: Experiments and model assessment. Materials 2019, 12, 1025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gomes, G.F.; de Almeida, F.A.; Ancelotti, A.C.; da Cunha, S.S. Inverse structural damage identification problem in CFRP laminated plates using SFO algorithm based on strain fields. Eng. Comput. 2021, 37, 3771–3791. [Google Scholar] [CrossRef]
- Uthaman, A.; Xian, G.; Thomas, S.; Wang, Y.; Zheng, Q.; Liu, X. Durability of an epoxy resin and its carbon fiber-reinforced polymer composite upon immersion in water, acidic, and alkaline solutions. Polymers 2020, 12, 614. [Google Scholar] [CrossRef] [Green Version]
- Stanciu, M.D.; Teodorescu Draghicescu, H.; Tamas, F.; Terciu, O.M. Mechanical and Rheological Behaviour of Composites Reinforced with Natural Fibres. Polymers 2020, 12, 1402. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, W.; Liu, L.; Xu, K.; Luo, G.; Zhao, Z. Experimental investigation on high-velocity impact damage and compression after impact behavior of 2D and 3D textile composites. Compos. Struct. 2022, 303, 116256. [Google Scholar] [CrossRef]
- Elmarakbi, A.; Mollón, V.; Bonhomme, J.; Viña, J.; Argüelles, A. Ch. 10. Fracture and Failure Mechanisms for Different Loading Modes in Unidirectional Carbon Fibre/Epoxy Composites. In Advanced Composite Materials for Automotive Applications: Structural Integrity and Crashworthiness; John Wiley & Sons Ltd.: West Sussex, UK, 2013; Chapter 10. [Google Scholar] [CrossRef]
- Romanowicz, M. A numerical approach for predicting the failure locus of fiber reinforced composites under combined transverse compression and axial tension. Comp. Mater. Sci. 2012, 51, 7–12. [Google Scholar] [CrossRef]
- Brod, M.; Dean, A.; Scheffler, S.; Gerendt, C.; Rolfes, R. Numerical modeling and experimental validation of fatigue damage in Cross-Ply CFRP composites under inhomogeneous stress states. Compos. Part B-Eng. 2020, 200, 108050. [Google Scholar] [CrossRef]
- Okabe, T.; Imamura, H.; Sato, Y.; Higuchi, R.; Koyanagi, J.; Talreja, R. Experimental and numerical studies of initial cracking in CFRP cross-ply laminates. Compos. Part A-Appl. Sci. 2015, 68, 81–89. [Google Scholar] [CrossRef]
- Dos Santos, D.J.; Carastan, D.J.; Tavares, L.B.; Batalha, G.F. Ch.2.03—Polymeric Materials Characterization and Modeling. In Comprehensive Materials Processing; Hashmi, S., Batalha, G.F., Van Tyne, C.J., Yilbas, B., Eds.; Elsevier: Oxford, UK, 2014; pp. 37–63. [Google Scholar]
- Šturm, R.; Grimberg, R.; Savin, A.; Grum, J. Destructive and nondestructive evaluations of the effect of moisture absorption on the mechanical properties of polyester-based composites. Compos. Part B-Eng. 2015, 71, 10–16. [Google Scholar] [CrossRef]
- Van de Werken, N.; Tekinalp, H.; Khanbolouki, P.; Ozcan, S.; Williams, A.; Tehrani, M. Additively manufactured carbon fiber-reinforced composites: State of the art and perspective. Addit. Manuf. 2020, 31, 100962. [Google Scholar] [CrossRef]
- Bhatt, A.T.; Gohil, P.P.; Chaudhary, V. Primary manufacturing processes for fiber reinforced composites: History, development & future research trends. IOP Conf. Ser.-Mat. Sci. Eng. 2018, 330, 012107. [Google Scholar] [CrossRef]
- Eliasson, S.; Karlsson Hagnell, M.; Wennhage, P.; Barsoum, Z. A Statistical Porosity Characterization Approach of Carbon-Fiber-Reinforced Polymer Material Using Optical Microscopy and Neural Network. Materials 2022, 15, 6540. [Google Scholar] [CrossRef] [PubMed]
- Kastner, J.; Plank, B.; Salaberger, D.; Sekelja, J. Defect and porosity determination of fibre reinforced polymers by X-ray computed tomography. In 2nd International Symposium on NDT in Aerospace; NDT: Hamburg, Germany, 2010; pp. 1–12. [Google Scholar]
- Bergant, Z.; Savin, A.; Grum, J. Effects of manufacturing technology on static, multi-frequency dynamic mechanical analysis and fracture energy of cross-ply and quasi-isotropic carbon/epoxy laminates. Polym. Polym. Compos. 2018, 26, 358–370. [Google Scholar] [CrossRef]
- Morgan, P. Carbon Fibers and Their Composites; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- ASTM D2584 2002; Standard Test Method for Ignition Loss of Cured Reinforced Resins. ASTM International: West Conshohocken, PA, USA, 2002.
- Boisse, P.; Huang, J.; Guzman-Maldonado, E. Analysis and modeling of wrinkling in composite forming. J. Compos. Sci. 2021, 5, 81. [Google Scholar] [CrossRef]
- Iosipescu, N. New Accurate Procedure for Single Shear Testing of Metals. J. Mater. 1967, 2, 537–566. [Google Scholar]
- Vlachakis, K.; Reygner, S.; Tibolt, M.; Vayas, I. Experimental investigations on rolled angle sections reinforced with CFRP plates. Ce/Papers 2021, 4, 229–236. [Google Scholar] [CrossRef]
- El-Hajjar, R.; Haj-Ali, R. In-plane shear testing of thick-section pultruded FRP composites using a modified Arcan fixture. Compos. Part B-Eng. 2004, 35, 421–428. [Google Scholar] [CrossRef]
- Hale, P.; Ng, E.G. Non-linear material characterization of CFRP with FEM utilizing cohesive surface considerations validated with effective tensile test fixturing. Mater. Today Commun. 2020, 23, 100872. [Google Scholar] [CrossRef]
- Koumoulos, E.P.; Trompeta, A.F.; Santos, R.M.; Martins, M.; Santos, C.M.D.; Iglesias, V.; Böhm, R.; Gong, G.; Chiminelli, A.; Verpoest, I.; et al. Research and development in carbon fibers and advanced high-performance composites supply chain in Europe: A roadmap for challenges and the industrial uptake. J. Compos. Sci. 2019, 3, 86. [Google Scholar] [CrossRef] [Green Version]
- Stamopoulos, A.G.; Tserpes, K.I.; Dentsoras, A.J. Quality assessment of porous CFRP specimens using X-ray Computed Tomography data and Artificial Neural Networks. Compos. Struct. 2018, 192, 327–335. [Google Scholar] [CrossRef]
- Savin, A.; Craus, M.L.; Turchenko, V.; Bruma, A.; Dubos, P.A.; Malo, S.; Konstantinova, T.E.; Burkhovetsky, V.V. Monitoring techniques of cerium stabilized zirconia for medical prosthesis. Appl. Sci. 2015, 5, 1665–1682. [Google Scholar] [CrossRef]
- NIST/SEMATECH e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook (accessed on 23 August 2022).
- Clyne, T.W.; Hull, D. An Introduction to Composite Materials; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Halpin, J.C.; Tsai, S.W. Effect of Environmental Factors on Composite Materials; Air Force Tech. Rep. AFML-TR-67-423; Wright Aeronautical Laboratories: Dayton, OH, USA, 1967. [Google Scholar]
- Engblom, J.J. Stress and Failure Analysis of Laminated Composite Structures; PDH Center: Faifax, VA, USA, 2012. [Google Scholar]












| Stacking Sequence | |||||
|---|---|---|---|---|---|
| [0]8 | [(45/0)2]s | ||||
| d (mm) | S1.1: 1.98 and S1.2: 2.0 | S2.1: 2.0 and S.2.2: 2.04 | |||
| Vf (%) | 45 | 47 | 44 | 46 | |
| Tension | E1 [GPa] | 33 | |||
| X1T [MPa] | 481 | 460 | |||
| ε1T [%] | 0.862 | ||||
| Ex [GPa] | 22.6 | ||||
| σxT [MPa] | 382 | 398 | |||
| εxT [%] | 1.015 | ||||
| Compression | E1 [GPa] | 37 | |||
| X1C [MPa] | 420 | ||||
| ε1C [%] | 0.9 | ||||
| Ex [GPa] | 28.6 | ||||
| σxC [MPa] | 312 | ||||
| εxC [%] | 1.08 | ||||
| Sample | σ [MPa] | τ [MPa] | X11 [MPa] | X12 [MPa] |
|---|---|---|---|---|
| S1.1 | 139.42 | 139.42 | 481 | 226.325 |
| S1.2 | 109.59 | 109.59 | 460 | 156 |
| S2.1 | 160 | 160 | 382 | 229.5 |
| S2.2 | 158 | 158 | 398 | 225 |
| Sample | The Semi-Axes of the Ellipse Which Delimits the Area Considered Safe | c1 | |
|---|---|---|---|
| X11/c1 [MPa] | X12/c1 [MPa] | ||
| S1.1 | 481/c1 = 327.43 | 226/c1 = 154.06 | 1.46 |
| S1.2 | 460/c1 = 343.28 | 156/c1 = 116.41 | 1.34 |
| S2.1 | 382/c1 = 313.11 | 229/c1 = 187.70 | 1.22 |
| S2.2 | 398/c1 = 310.93 | 225/c1 = 175.78 | 1.28 |
| Sample | The Semi-Axes of the Ellipse Which Delimits the Area Considered Safe | c2 | |
|---|---|---|---|
| X11/c2 [MPa] | X12/c2 [MPa] | ||
| S1.1 | 327.43/c2 = 262 | 154.06/c2 = 123.39 | 1.248 |
| S1.2 | 343.28/c2 = 266 | 116.41/c2 = 90.24 | 1.29 |
| S2.1 | 313.11/c2 = 274.65 | 187.70/c2 = 164.64 | 1.14 |
| S2.2 | 310.93/c2 = 290.58 | 175.78/c2 = 164.28 | 1.068 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mititelu, I.; Petrișor, S.M.; Savin, A.; Šturm, R.; Bergant, Z.; Steigmann, R.; Stanciu, M.D.; Bârsănescu, P.D. Multi-Criteria Evaluation of the Failure of CFRP Laminates for Frames in the Automotive Industry. Polymers 2022, 14, 4507. https://doi.org/10.3390/polym14214507
Mititelu I, Petrișor SM, Savin A, Šturm R, Bergant Z, Steigmann R, Stanciu MD, Bârsănescu PD. Multi-Criteria Evaluation of the Failure of CFRP Laminates for Frames in the Automotive Industry. Polymers. 2022; 14(21):4507. https://doi.org/10.3390/polym14214507
Chicago/Turabian StyleMititelu, Ionuț, Silviu Mihai Petrișor, Adriana Savin, Roman Šturm, Zoran Bergant, Rozina Steigmann, Mariana Domnica Stanciu, and Paul Doru Bârsănescu. 2022. "Multi-Criteria Evaluation of the Failure of CFRP Laminates for Frames in the Automotive Industry" Polymers 14, no. 21: 4507. https://doi.org/10.3390/polym14214507
APA StyleMititelu, I., Petrișor, S. M., Savin, A., Šturm, R., Bergant, Z., Steigmann, R., Stanciu, M. D., & Bârsănescu, P. D. (2022). Multi-Criteria Evaluation of the Failure of CFRP Laminates for Frames in the Automotive Industry. Polymers, 14(21), 4507. https://doi.org/10.3390/polym14214507