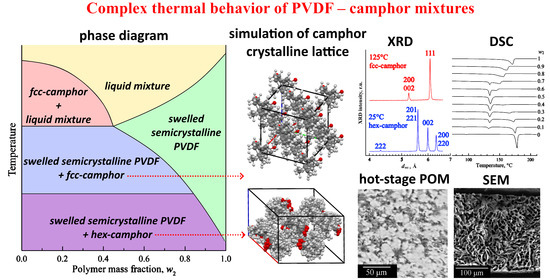
A New Look at the Structure and Thermal Behavior of Polyvinylidene Fluoride–Camphor Mixtures
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Phase Diagram by the Optical Method
3.2. Analysis of the DSC Data
3.3. Comparison of the Optical and DSC Data
3.4. Solid–Solid Phase Transition in Camphor
3.5. Crystallization in the Pre-Homogenized Mixtures
3.6. Morphology of the Capillary-Porous Bodies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, Y.; Lin, Y.; Ma, W.; Wang, X. A review on microporous polyvinylidene fluoride membranes fabricated via thermally induced phase separation for MF/UF application. J. Membr. Sci. 2021, 639, 119759. [Google Scholar] [CrossRef]
- Su, J.F.; Beltsios, K.G.; Li, P.H.; Cheng, L.P. Facile formation of symmetric microporous PVDF membranes via vapor-induced phase separation of metastable dopes. Colloids Surfaces A Physicochem. Eng. Asp. 2022, 634, 128012. [Google Scholar] [CrossRef]
- Sun, Q.; Yang, Z.; Hu, C.; Li, C.; Yan, G.; Wang, Z. Facile preparation of superhydrophobic PVDF microporous membranes with excellent anti-fouling ability for vacuum membrane distillation. J. Membr. Sci. 2020, 605, 118106. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, C.; Huang, Q.; Liu, H.; Zhao, J. Progress on polymeric hollow fiber membrane preparation technique from the perspective of green and sustainable development. Chem. Eng. J. 2021, 403, 126295. [Google Scholar] [CrossRef]
- Yang, C.; Han, N.; Wang, W.; Zhang, W.; Han, C.; Cui, Z.; Zhang, X. Fabrication of a PPS microporous membrane for efficient water-in-oil emulsion separation. Langmuir 2018, 34, 10580–10590. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.M.; Rodrigue, D. A review on porous polymeric membrane preparation. Part I: Production techniques with polysulfone and poly (vinylidene fluoride). Polymers 2019, 11, 1160. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.M.; Rodrigue, D. A review on porous polymeric membrane preparation. Part II: Production techniques with polyethylene, polydimethylsiloxane, polypropylene, polyimide, and polytetrafluoroethylene. Polymers 2019, 11, 1310. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Zhang, Z.; Ma, L.; Xu, X.; Zhang, P.; Yu, H. Explorations of complex thermally induced phase separation (C-TIPS) method for manufacturing novel diphenyl ether polysulfate flat microporous membranes. J. Membr. Sci. 2022, 659, 120739. [Google Scholar] [CrossRef]
- Usman, M.; Ahmed, A.; Yu, B.; Peng, Q.; Shen, Y.; Cong, H. A review of different synthetic approaches of amorphous intrinsic microporous polymers and their potential applications in membrane-based gases separation. Eur. Polym. J. 2019, 120, 109262. [Google Scholar] [CrossRef]
- Yu, S.; Li, S.; Liu, Y.; Cui, S.; Shen, X. High-performance microporous polymer membranes prepared by interfacial polymerization for gas separation. J. Membr. Sci. 2019, 573, 425–438. [Google Scholar] [CrossRef]
- Xie, K.; Fu, Q.; Qiao, G.G.; Webley, P.A. Recent progress on fabrication methods of polymeric thin film gas separation membranes for CO2 capture. J. Membr. Sci. 2019, 572, 38–60. [Google Scholar] [CrossRef]
- Molavi, F.; Barzegar-Jalali, M.; Hamishehkar, H. Polyester based polymeric nano and microparticles for pharmaceutical purposes: A review on formulation approaches. J. Control. Release 2020, 320, 265–282. [Google Scholar] [CrossRef] [PubMed]
- Amoyav, B.; Benny, O. Microfluidic based fabrication and characterization of highly porous polymeric microspheres. Polymers 2019, 11, 419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andhariya, J.V.; Jog, R.; Shen, J.; Choi, S.; Wang, Y.; Zou, Y.; Burgess, D.J. Development of Level A in vitro-in vivo correlations for peptide loaded PLGA microspheres. J. Control. Release 2019, 308, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Cheng, X.; Li, Y.; You, J. Microsphere with narrow nanopores: Fabrication in PVDF/PMMA/PLLA blend and enhanced adsorption/separation performances. Appl. Surf. Sci. 2021, 566, 150673. [Google Scholar] [CrossRef]
- Bashir, M.S.; Jiang, X.; Kong, X.Z. Porous polyurea microspheres with Pd immobilized on surface and their catalytic activity in 4-nitrophenol reduction and organic dyes degradation. Eur. Polym. J. 2020, 129, 109652. [Google Scholar] [CrossRef]
- Mironov, A.V.; Mironova, O.A.; Syachina, M.A.; Popov, V.K. 3D printing of polylactic-co-glycolic acid fiber scaffolds using an antisolvent phase separation process. Polymer 2019, 182, 121845. [Google Scholar] [CrossRef]
- Ogueri, K.S.; Jafari, T.; Escobar Ivirico, J.L.; Laurencin, C.T. Polymeric biomaterials for scaffold-based bone regenerative engineering. Regen. Eng. Transl. Med. 2019, 5, 128–154. [Google Scholar] [CrossRef]
- Tao, T.; Deng, Y.; Liang, Z.; Liang, B.; Yao, Y.; Li, P.; Lu, S.; Chen, Y. Synthesis of porous polyvinylidene fluoride (PVDF) microspheres and their application in lithium sulfur batteries. Mater. Lett. 2017, 188, 180–183. [Google Scholar] [CrossRef]
- Sultana, A.; Sadhukhan, P.; Alam, M.M.; Das, S.; Middya, T.R.; Mandal, D. Organo-Lead Halide Perovskite Induced Electroactive β-Phase in Porous PVDF Films: An Excellent Material for Photoactive Piezoelectric Energy Harvester and Photodetector. ACS Appl. Mater. Interfaces 2018, 10, 4121–4130. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Basko, A.V. Formation of porous microspheres from semicrystalline polymer solutions: Diffusion- controlled and local phase separation. Polym. Technol. Mater. 2022, 61, 1279–1291. [Google Scholar] [CrossRef]
- Löffler, R.J.G.; Hanczyc, M.M.; Gorecki, J. A camphene-camphor-polymer composite material for the production of superhydrophobic absorbent microporous foams. Sci. Rep. 2022, 12, 243. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.T.; Wang, H.H.; Kim, J.F.; Lee, J.; Kim, J.S.; Drioli, E.; Lee, Y.M. Tailoring nonsolvent-thermally induced phase separation (N-TIPS) effect using triple spinneret to fabricate high performance PVDF hollow fiber membranes. J. Membr. Sci. 2018, 559, 117–126. [Google Scholar] [CrossRef]
- Zuo, J.H.; Li, Z.K.; Wei, C.; Yan, X.; Chen, Y.; Lang, W.Z. Fine tuning the pore size and permeation performances of thermally induced phase separation (TIPS) -prepared PVDF membranes with saline water as quenching bath. J. Membr. Sci. 2019, 577, 79–90. [Google Scholar] [CrossRef]
- Su, Y.; Chen, C.; Li, Y.; Li, J. PVDF membrane formation via thermally induced phase separation. J. Macromol. Sci.–Pure Appl. Chem. 2007, 44, 99–104. [Google Scholar] [CrossRef]
- Kim, J.F.; Jung, J.T.; Wang, H.H.; Lee, S.Y.; Moore, T.; Sanguineti, A.; Drioli, E.; Lee, Y.M. Microporous PVDF membranes via thermally induced phase separation (TIPS) and stretching methods. J. Membr. Sci. 2016, 509, 94–104. [Google Scholar] [CrossRef]
- Li, X.; Lu, X. Morphology of polyvinylidene fluoride and its blend in thermally induced phase separation process. J. Appl. Polym. Sci. 2006, 101, 2944–2952. [Google Scholar] [CrossRef]
- Zhao, J.; Chong, J.Y.; Shi, L.; Wang, R. Explorations of combined nonsolvent and thermally induced phase separation (N-TIPS) method for fabricating novel PVDF hollow fiber membranes using mixed diluents. J. Membr. Sci. 2019, 572, 210–222. [Google Scholar] [CrossRef]
- Gu, M.; Zhang, J.; Wang, X.; Tao, H.; Ge, L. Formation of poly(vinylidene fluoride) (PVDF) membranes via thermally induced phase separation. Desalination 2006, 192, 160–167. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.L.; Tian, Y.; Lin, Y.; Tian, F. Morphologies and crystalline forms of polyvinylidene fluoride membranes prepared in different diluents by thermally induced phase separation. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 2468–2475. [Google Scholar] [CrossRef]
- Ji, G.L.; Du, C.H.; Zhu, B.K.; Xu, Y.Y. Preparation of porous PVDF membrane via thermally induced phase separation with diluent mixture of DBP and DEHP. J. Appl. Polym. Sci. 2007, 105, 1496–1502. [Google Scholar] [CrossRef]
- Guenet, J.M.; Parmentier, J.; Daniel, C. Porous materials from polyvinylidene fluoride/solvent molecular compounds. Soft Mater. 2011, 9, 280–294. [Google Scholar] [CrossRef]
- Dasgupta, D.; Manna, S.; Malik, S.; Rochas, C.; Guenet, J.M.; Nandi, A.K. Thermoreversible gelation of Poly(vinylidene fluoride)—Camphor system. Macromol Symp. 2005, 222, 175–180. [Google Scholar] [CrossRef]
- Dasgupta, D.; Manna, S.; Malik, S.; Rochas, C.; Guenet, J.M.; Nandi, A.K. Thermodynamic structural and morphological investigation of poly(vinylidene fluoride)-camphor systems, preparing porous gels from a solid solvent. Macromolecules 2005, 38, 5602–5608. [Google Scholar] [CrossRef]
- Dasgupta, D.; Nandi, A.K. Multiporosity in dried poly(vinylidene fluoride)—Camphor systems: Effect of drying method on porosity. Macromolecules 2007, 40, 2008–2018. [Google Scholar] [CrossRef]
- Basko, A.V.; Pochivalov, K.V.; Bazanov, A.V.; Shandryuk, G.A.; Ezhov, A.A.; Artemov, V.V.; Kudryavtsev, Y.V. Phase diagram of the low-density polyethylene–dimethyl terephthalate system: A new topology. Thermochim. Acta 2020, 684, 178499. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Basko, A.V.; Lebedeva, T.N.; Ilyasova, A.N.; Golovanov, R.Y.; Yurov, M.Y.; Shandryuk, G.A.; Ezhov, A.A.; Artemov, V.V.; Kudryavtsev, Y.V. Analysis of the thermal behavior of polypropylene-camphor mixtures for understanding the pathways to polymeric membranes via thermally induced phase separation. J. Phys. Chem. B 2019, 123, 10533–10546. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Basko, A.V.; Kudryavtsev, Y.V. Binary mixtures of semicrystalline polymers with low-molecular-mass compounds: Thermal behaviour and phase structure. Russ. Chem Rev. 2020, 89, 311–338. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Basko, A.V.; Lebedeva, T.N.; Ilyasova, A.N.; Yurov, M.Y.; Golovanov, R.Y.; Artemov, V.V.; Volkov, V.V.; Ezhov, A.A.; Volkov, A.V.; et al. Thermally induced phase separation in semicrystalline polymer solutions: How does the porous structure actually arise? Mater. Today Commun. 2021, 28, 102558. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Lebedeva, T.N.; Ilyasova, A.N.; Basko, A.V.; Kudryavtsev, Y.V. A new look at the semicrystalline polymer–liquid systems: Phase diagrams low-density polyethylene–n-alkanes. Fluid Phase Equilib. 2018, 471, 1–7. [Google Scholar] [CrossRef]
- Ilyasova, A.N.; Lebedeva, T.N.; Shilov, A.N.; Pochivalov, K.V. Estimation of the thermodynamic quality of alkylbenzenes with respect to low density polyethylene. Polym. Sci. Ser. A 2018, 59, 839–843. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Basko, A.V.; Denisova, Y.I.; Shandryuk, G.A.; Ezhov, A.A.; Artemov, V.V.; Kudryavtsev, Y.V. Isotactic polypropylene–1,2,4,5-tetrachlorobenzene: Porous bodies via thermally induced phase separation. J. Therm. Anal. Calorim. 2019, 138, 2481–2489. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Basko, A.V.; Lebedeva, T.N.; Antina, L.A.; Golovanov, R.Y.; Artemov, V.V.; Ezhov, A.A.; Kudryavtsev, Y.V. Low-density polyethylene-thymol: Thermal behavior and phase diagram. Thermochim. Acta 2018, 659, 113–120. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Kudryavtsev, Y.V.; Lebedeva, T.N.; Antina, L.A.; Ilyasova, A.N.; Yurov, M.Y.; Basko, A.V.; Zavadskii, A.E. Poly[3,3-bis(azidomethyl)oxetane]–2,4-dinitro-2,4-diazapentane: Thermal behavior and peculiarities of crystallization. J. Therm. Anal. Calorim. 2018, 131, 2225–2233. [Google Scholar] [CrossRef]
- Anderson, J.E.; Slichter, W.P. Nuclear magnetic relaxation in camphor. J. Chem. Phys. 1967, 41, 1922–1928. [Google Scholar] [CrossRef]
- Mjojo, C.C. Order–disorder phenomena. Order–disorder phenomena Part 2.—Order–disorder phase equilibria in D- and L-systems of camphor and related compounds. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1979, 75, 692–703. [Google Scholar] [CrossRef]
- Prout, K. Molecules in motion: A study in the synergy of X-ray diffraction and solid state NMR. Croat. Chem. Acta 2002, 75, 817–833. [Google Scholar]
- Rietveld, I.B.; Barrio, M.; Veglio, N.; Espeau, P.; Tamarit, J.L.; Céolin, R. Temperature and composition-dependent properties of the two-component system d- and l-camphor at ‘ordinary’ pressure. Thermochim. Acta 2010, 511, 43–50. [Google Scholar] [CrossRef]
- Chandra, G.; Murthy, S.S.N. Dielectric and thermodynamic study of camphor and borneol enantiomers and their binary systems. Thermochim. Acta 2018, 666, 241–252. [Google Scholar] [CrossRef]
- Ruggiero, M.T.; Zhang, W.; Bond, A.D.; Mittleman, D.M.; Zeitler, J.A. Uncovering the connection between low-frequency dynamics and phase transformation phenomena in molecular solids. Phys. Rev. Lett. 2018, 120, 196002. [Google Scholar] [CrossRef] [Green Version]
- Wallerant, M.F. Sue de polymorphisme du camphre. Comp. Rend. Hebd. Seances Acad. Sci. 1914, 158, 77–78. [Google Scholar]
- Yager, W.A.; Morgan, S.O. Trarisitions in camphor and chemically related compounds. 1. Dipole rotation in crystalline solids. J. Am. Chem. Soc. 1935, 57, 2017–2078. [Google Scholar] [CrossRef]
- Von Schafer, K.L.; Wagner, U. Uber die umwandlung im system d-l-campher. Z. Elektrochem. 1958, 62, 328–335. [Google Scholar]
- Figoli, A.; Simone, S.; Criscuoli, A.; Al-Jlil, S.A.; Al Shabouna, F.S.; Al-Romaih, H.S.; Di Nicolo, E.; Al-Harbi, O.A.; Drioli, E. Hollow fibers for seawater desalination from blends of PVDF with different molecular weights: Morphology, properties and VMD performance. Polymer 2014, 55, 1296–1306. [Google Scholar] [CrossRef]
- Hassankiadeh, N.T.; Cui, Z.; Kim, J.H.; Shin, D.W.; Sanguineti, A.; Arcella, V.; Lee, Y.M.; Drioli, E. PVDF hollow fiber membranes prepared from green diluent via thermally induced phase separation: Effect of PVDF molecular weight. J. Membr. Sci. 2014, 471, 237–246. [Google Scholar] [CrossRef]
- Haponska, M.; Trojanowska, A.; Nogalska, A.; Jastrzab, R.; Gumi, T.; Tylkowski, B. PVDF membrane morphology—influence of polymer molecular weight and preparation temperature. Polymers 2017, 9, 718. [Google Scholar] [CrossRef] [Green Version]
- Nakagawa, K.; Ishida, Y. Annealing effects in poly(vinylidene fluoride) as revealed by specific volume measurements, differential scanning calorimetry, and electron microscopy. J. Polym. Sci. Polym. Phys. Ed. 1973, 11, 2153–2171. [Google Scholar] [CrossRef]
- Pochivalov, K.V.; Vyalova, A.N.; Golovanov, R.Y.; Mizerovskii, L.N. On the procedure of constructing phase diagrams of partially crystalline polymer-liquid systems. Russ. J. Appl. Chem. 2012, 85, 153–155. [Google Scholar] [CrossRef]
- Basko, A.V.; Pochivalov, K.V.; Chalykh, T.I.; Shandryuk, G.A.; Ezhov, A.A.; Artemov, V.V.; Kudryavtsev, Y.V. Combining optical microscopy, turbidimetry, and DSC to study structural transformations in the mixtures of semicrystalline polymers with low-molar-mass crystallizable substances. Thermochim. Acta 2020, 690, 178671. [Google Scholar] [CrossRef]
- Smith, P.; Penning, A.J. Eutectic solidification of the pseudo binary system of polyethylene and 1,2,4,5-tetrachlorobenzene. J. Mater. Sci. 1976, 11, 1450–1458. [Google Scholar] [CrossRef]
- Smith, P.; Pennings, A.J. Eutectic crystallization of pseudo binary systems of polyethylene and high melting diluents. Polymer 1974, 15, 413–419. [Google Scholar] [CrossRef]
- Hagström, B. Mechanical properties and phase diagrams of alloys of high density polyethylene with some low molecular weight organic compounds. J. Mater. Sci. 1985, 20, 3906–3916. [Google Scholar] [CrossRef]
- Wittmann, J.C.; Manley, R.S.J. Polymer–monomer binary mixtures. Eutectic crystallization of poly(ethylene oxide)–trioxane mixtures. J. Polym. Sci. Polym. Phys. Ed. 1977, 15, 2277–2280. [Google Scholar] [CrossRef]
- Zhu, X.; Xiao, Y.; He, P.; Yan, D.; Fang, Y. Eutectic-forming binary system of poly(ethylene oxide) and p-hydroxybenzaldehyde. Polym Int. 2003, 52, 813–818. [Google Scholar] [CrossRef]
- Karolewicz, B.; Gajda, M.; Pluta, J.; Górniak, A. Dissolution study and thermal analysis of fenofibrate–Pluronic F127 solid dispersions. J. Therm. Anal. Calorim. 2016, 125, 751–757. [Google Scholar] [CrossRef] [Green Version]
- Kuttich, B.; Matt, A.; Appel, C.; Stühn, B. X-ray scattering study on the crystalline and semi-crystalline structure of water/PEG mixtures in their eutectic phase diagram. Soft Matter 2020, 16, 10260–10267. [Google Scholar] [CrossRef]
- Rezasoltani, E.; Guilbert, A.A.Y.; Yan, J.; Rodríguez-Martínez, X.; Azzouzi, M.; Eisner, F.; Tuladhar, S.M.; Hamid, Z.; Wadsworth, A.; McCulloh, I.; et al. Correlating the phase behavior with the device performance in binary poly-3-hexylthiophene: Nonfullerene acceptor blend using optical probes of the microstructure. Chem. Mater. 2020, 32, 8294–8305. [Google Scholar] [CrossRef]
- Smith, P.; Alberda van Edenstein, G.O.R.; Pennings, A.J. Eutectic solidification of the quasi binary system of isotactic polypropylene and 1,2,4,5-tetrachlorobenzene. Br. Polym, J. 1977, 9, 258–263. [Google Scholar] [CrossRef]
- Basko, A.V.; Lebedeva, T.N.; Yurov, M.Y.; Pochivalov, K.V. The effect of physical state of thymol on the duration of its release from the mixture with a semicrystalline polymer: Thermodynamic aspects and kinetics of the process. Polym. Sci. Ser. A 2021, 64, 10–18. [Google Scholar] [CrossRef]
- Wunderlich, B. Reversible crystallization and the rigid–amorphous phase in semicrystalline macromolecules. Prog. Polym. Sci. 2003, 28, 383–450. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Zhou, Y.; Wang, C.; Zhang, X.-Z.; Deng, H. Covalent organic frameworks as favorable constructs for photodynamic therapy. Angew. Chem. Int. Ed. 2019, 58, 14213–14218. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Liu, Y.; Guo, Y.; Ma, L.; Liu, Y.; Zhou, C.; Yu, X.; Zhao, G. Lead-free sodium bismuth halide Cs2NaBiX6 double perovskite nanocrystals with highly efficient photoluminescence. Chem. Eng. J. 2020, 397, 125367. [Google Scholar] [CrossRef]
- Wang, C.; Ma, L.; Wang, S.; Zhao, G. Efficient photoluminescence of manganese-doped two-dimensional chiral alloyed perovskites. J. Phys. Chem. Lett. 2021, 12, 50. [Google Scholar] [CrossRef]
- Wunderlich, B. Macromolecular Physics: Crystal Melting; Academic Press: New York, NY, USA, 1980; Volume 3. [Google Scholar]
- Melnikov, A.P.; Rosenthal, M.; Rodygin, A.I.; Doblas, D.; Anokhin, D.V.; Burghammer, M.; Ivanov, D.A. Re-exploring the double-melting behavior of semirigid-chain polymers with an in-situ combination of synchrotron nano-focus X-ray scattering and nanocalorimetry. Eur. Polym. J. 2016, 81, 598–606. [Google Scholar] [CrossRef]
- Litvinov, V.; Deblieck, R.; Clair, C.; Van Den Fonteyne, W.; Lallam, A.; Kleppinger, R.; Ivanov, D.A.; Ries, M.E.; Boerakker, M. Molecular structure, phase composition, melting behavior, and chain entanglements in the amorphous phase of high-density polyethylenes. Macromolecules 2020, 53, 5418–5433. [Google Scholar] [CrossRef]
- Rozanski, A.; Safandowska, M.; Krajenta, A. DSC/SAXS analysis of the thickness of lamellae of semicrystalline polymers-restrictions in the case of materials with swollen amorphous phase. Polym. Test. 2018, 65, 189–196. [Google Scholar] [CrossRef]
- Rozanski, A.; Galeski, A. Plastic yielding of semicrystalline polymers affected by amorphous phase. Int. J. Plast. 2013, 41, 14–29. [Google Scholar] [CrossRef]
- Polińska, M.; Rozanski, A.; Galeski, A.; Bojda, J. The modulus of the amorphous phase of semicrystalline polymers. Macromolecules 2021, 54, 9113–9123. [Google Scholar] [CrossRef]
- Rozanski, A.; Galeski, A. Crystalline lamellae fragmentation during drawing of polypropylene. Macromolecules 2015, 48, 5310–5322. [Google Scholar] [CrossRef]
- Schulz, M.; Seidlitz, A.; Kurz, R.; Bärenwald, R.; Petzold, A.; Saalwächter, K.; Thurn-Albrecht, T. The underestimated effect of intracrystalline chain dynamics on the morphology and stability of semicrystalline polymers. Macromolecules 2018, 51, 8377–8385. [Google Scholar] [CrossRef]
- Zhou, H.; Wilkes, G.L. Comparison of lamellar thickness and its distribution determined from d.s.c., SAXS, TEM and AFM for high-density polyethylene films having a stacked lamellar morphology. Polymer 1997, 38, 5735–5747. [Google Scholar] [CrossRef]
- Mizerovskii, L.N.; Pochivalov, K.V.; Afanaseva, V.V. A semicrystalline polymer as a metastable microheterogeneous liquid. Polym. Sci. Ser. A 2010, 52, 973–984. [Google Scholar] [CrossRef]
- Rietveld, I.B.; Barrio, M.; Espeau, P.; Tamarit, J.L.; Céolin, R. Topological and experimental approach to the pressure-temperature-composition phase diagram of the binary enantiomer system d- and l-Camphor. J. Phys. Chem. B 2011, 115, 1672–1678. [Google Scholar] [CrossRef] [PubMed]
- Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Wang, G.; Harrison, I.R. Polymer melting: Heating rate effects on DSC melting peaks. Thermochim. Acta 1994, 231, 203–213. [Google Scholar] [CrossRef]
- Toda, A. Heating rate dependence of melting peak temperature examined by DSC of heat flux type. J. Therm. Anal. Calorim. 2016, 123, 1795–1808. [Google Scholar] [CrossRef]
- Timmermans, J. Plastic crystals: A hictorical review. J. Phys. Chem. Solids 1961, 18, 1–8. [Google Scholar] [CrossRef]
- Das, S.; Mondal, A.; Reddy, C.M. Harnessing molecular rotations in plastic crystals: A Holistic view for crystal engineering of adaptive soft materials. Chem. Soc. Rev. 2020, 49, 8878–8895. [Google Scholar] [CrossRef]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pochivalov, K.V.; Basko, A.V.; Lebedeva, T.N.; Ilyasova, A.N.; Shandryuk, G.A.; Snegirev, V.V.; Artemov, V.V.; Ezhov, A.A.; Kudryavtsev, Y.V. A New Look at the Structure and Thermal Behavior of Polyvinylidene Fluoride–Camphor Mixtures. Polymers 2022, 14, 5214. https://doi.org/10.3390/polym14235214
Pochivalov KV, Basko AV, Lebedeva TN, Ilyasova AN, Shandryuk GA, Snegirev VV, Artemov VV, Ezhov AA, Kudryavtsev YV. A New Look at the Structure and Thermal Behavior of Polyvinylidene Fluoride–Camphor Mixtures. Polymers. 2022; 14(23):5214. https://doi.org/10.3390/polym14235214
Chicago/Turabian StylePochivalov, Konstantin V., Andrey V. Basko, Tatyana N. Lebedeva, Anna N. Ilyasova, Georgiy A. Shandryuk, Vyacheslav V. Snegirev, Vladimir V. Artemov, Alexander A. Ezhov, and Yaroslav V. Kudryavtsev. 2022. "A New Look at the Structure and Thermal Behavior of Polyvinylidene Fluoride–Camphor Mixtures" Polymers 14, no. 23: 5214. https://doi.org/10.3390/polym14235214
APA StylePochivalov, K. V., Basko, A. V., Lebedeva, T. N., Ilyasova, A. N., Shandryuk, G. A., Snegirev, V. V., Artemov, V. V., Ezhov, A. A., & Kudryavtsev, Y. V. (2022). A New Look at the Structure and Thermal Behavior of Polyvinylidene Fluoride–Camphor Mixtures. Polymers, 14(23), 5214. https://doi.org/10.3390/polym14235214