Mechanical and Thermal Behaviours of Weft-Knitted Spacer Fabric Structure with Inlays for Insole Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Inlaid Foam
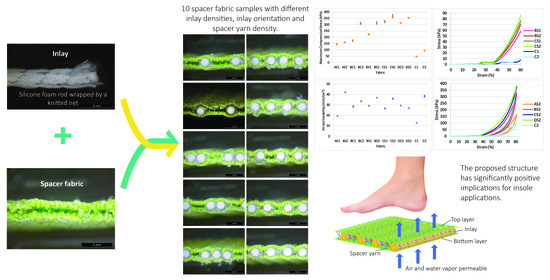
2.2. Inlaid Spacer Fabric Samples
2.3. Evaluation of Mechanical and Thermal Behaviours of Fabric
2.3.1. Physical Properties
2.3.2. Compression and Impact Force Reduction
2.3.3. Thermal and Evaporative Resistance
2.3.4. Statistical Analysis
3. Results and Discussion
3.1. Air Permeability
3.2. Compression Behaviour
3.2.1. Effect of Inlay Density
3.2.2. Effect of Spacer Yarn Density
3.2.3. Effect of Inlay Orientation
3.3. Impact Force Reduction
3.4. Thermal Comfort Properties
3.4.1. Evaporative Resistance
3.4.2. Thermal Resistance
4. Conclusions
- The high spacer yarn density of inlaid spacer fabric offers good air permeability. The size of the knitted loops on the surface layer are extended by the additional spacer yarn that allow air to flow through the material. Therefore, spacer fabric with a higher spacer yarn density has higher air permeability, and lower stitch density and fabric weight;
- For the mechanical properties, the compression resistance of the inlaid spacer fabric is largely increased by an increased number of inlays and spacer yarns while the absorbed compression energy in Stage II remains unchanged. The increased compression resistance is associated with the even distribution of forces exerted onto the flat surface of the fabric and the increased fabric stiffness. The effect of the inlay orientation on the compressive stress is less significant in this study. The fabric samples made with inlaid yarns embedded in a random orientation are stiffer than those with inlaid yarns embedded in a localized orientation;
- Meanwhile, spacer fabrics with higher inlay density and more spacer yarns can reduce higher impact forces. The inlay density is the key factor as the inlay foam rods can effectively reduce and absorb the impact forces for cushioning;
- The evaporative resistance performance of the inlay spacer fabrics is increased with inlay density and embedded in a localized orientation. On the other hand, the fabric thermal resistance is decreased with the higher inlay density for fabric with a high spacer yarn density. Samples with more spacer yarn have a lower stitch density in the surface layers which facilitates air passage, thus leading to low thermal resistance. Therefore, samples with more spacer yarns while embedded in a random orientation allow optimal moisture evaporation and reduce thermal discomfort of humidity to the wearers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Du, L.; Li, T.; Wu, S.; Zhu, H.F.; Zou, F.Y. Electrospun composite nanofibre fabrics containing green reduced Ag nanoparticles as an innovative type of antimicrobial insole. RSC Adv. 2019, 9, 2244–2251. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Santos, A.; Preece, S.; Nester, C.J. Evaluation of orthotic insoles for people with diabetes who are at-risk of first ulceration. J. Foot Ankle Res. 2019, 12, 35. [Google Scholar] [CrossRef] [PubMed]
- Niu, J.; Liu, J.; Zheng, Y.; Ran, L.; Chang, Z. Are arch-conforming insoles a good fit for diabetic foot? Insole customized design by using finite element analysis. Hum. Factors Ergon. Manuf. Serv. Ind. 2020, 30, 303–310. [Google Scholar] [CrossRef]
- Paton, J.; Glasser, S.; Collings, R.; Marsden, J. Getting the right balance: Insole design alters the static balance of people with diabetes and neuropathy. J. Foot Ankle Res. 2016, 9, 40. [Google Scholar] [CrossRef] [Green Version]
- Cham, M.B.; Mohseni-Bandpei, M.A.; Bahramizadeh, M.; Forogh, B.; Kalbasi, S.; Biglarian, A. Effects of vibro-medical insoles with and without vibrations on balance control in diabetic patients with mild-to-moderate peripheral neuropathy. J. Biomech. 2020, 103, 109656. [Google Scholar] [CrossRef]
- Messaoud, M.; Vaesken, A.; Aneja, A.; Schacher, L.; Adolphe, D.; Schaffhauser, J.-B.; Strehle, P. Physical and mechanical characterizations of recyclable insole product based on new 3D textile structure developed by the use of a patented vertical-lapping process. J. Ind. Text. 2015, 44, 497–512. [Google Scholar] [CrossRef]
- Rajan, T.P.; Sundaresan, S. Thermal comfort properties of plasma-treated warp-knitted spacer fabric for the shoe insole. J. Ind. Text. 2020, 49, 1218–1232. [Google Scholar] [CrossRef]
- Kumar, N.M.; Thilagavathi, G.; Periasamy, S. Development and characterization of warp knitted spacer fabrics for helmet comfort liner application. J. Ind. Text. 2020, 152808372093921. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, H. Application of Superabsorbent Spacer Fabrics as Exuding Wound Dressing. Polymers 2018, 10, 210. [Google Scholar] [CrossRef] [Green Version]
- Datta, M.K.; Behera, B.; Goyal, A. Characterization of Warp Knitted Spacer Fabric for Application in Sports Bra. Fibers Polym. 2019, 20, 1983–1991. [Google Scholar] [CrossRef]
- Du, Z.; Wu, Y.; Wu, Y.; He, L. Determination of pressure indices to characterize the pressure-relief property of spacer fabric based on a pressure pad system. Text. Res. J. 2016, 86, 1443–1451. [Google Scholar] [CrossRef]
- Yu, A.; Sukigara, S.; Yick, K.-L.; Li, P.-L. Novel weft-knitted spacer structure with silicone tube inlay for enhancing mechanical behavior. Mech. Adv. Mater. Struct. 2020, 1–12. [Google Scholar] [CrossRef]
- Du, Z.; Wu, Y.; Li, M.; He, L. Analysis of structure of warp-knitted spacer fabric on pressure indices. Fibers Polym. 2015, 16, 2491–2496. [Google Scholar] [CrossRef]
- Turki, S.; Ben Abdallah, S.; Ben Abdessalem, S. Development of composite materials reinforced with flat-knitted spacer fabrics. J. Text. Inst. 2018, 109, 1315–1321. [Google Scholar] [CrossRef]
- Zhao, T.; Long, H.; Yang, T.; Liu, Y. Cushioning properties of weft-knitted spacer fabrics. Text. Res. J. 2018, 88, 1628–1640. [Google Scholar] [CrossRef]
- Hamedi, M.; Salimi, P.; Jamshidi, N. Improving cushioning properties of a 3D weft knitted spacer fabric in a novel design with NiTi monofilaments. J. Ind. Text. 2020, 49, 1389–1410. [Google Scholar] [CrossRef]
- Yu, A.; Sukigara, S.; Shirakihara, M. Effect of Silicone Inlaid Materials on Reinforcing Compressive Strength of Weft-Knitted Spacer Fabric for Cushioning Applications. Polymers 2021, 13, 3645. [Google Scholar] [CrossRef] [PubMed]
- Li, N.W.; Ho, C.P.; Yick, K.L.; Zhou, J.Y. Influence of inlaid material, yarn and knitted structure on the net buoyant force and mechanical properties of inlaid knitted fabric for buoyant swimwear. Text. Res. J. 2021, 91, 1452–1466. [Google Scholar] [CrossRef]
- Azam, Z.; Jamshaid, H.; Nawab, Y.; Mishra, R.; Muller, M.; Choteborsky, R.; Kolar, V.; Tichy, M.; Petru, M. Influence of inlay yarn type and stacking sequence on mechanical performance of knitted uni-directional thermoplastic composite prepregs. J. Ind. Text. 2020, 152808372094772. [Google Scholar] [CrossRef]
- Siddique, H.F.; Mazari, A.A.; Havelka, A.; Mansoor, T.; Ali, A.; Azeem, M. Development of V-Shaped Compression Socks on Conventional Socks Knitting Machine. Autex Res. J. 2018, 18, 377–384. [Google Scholar] [CrossRef] [Green Version]
- Shabaridharan; Das, A. Study on heat and moisture vapour transmission characteristics through multilayered fabric ensembles. Fibers Polym. 2012, 13, 522–528. [Google Scholar] [CrossRef]
- Oswald, C.; Denhartog, E. Transient heat loss analysis of fabrics using a dynamic sweating guarded hot plate protocol. Text. Res. J. 2020, 90, 1130–1140. [Google Scholar] [CrossRef]
- Bagherzadeh, R.; Latifi, M.; Najar, S.S.; Tehran, M.A.; Gorji, M.; Kong, L. Transport properties of multi-layer fabric based on electrospun nanofiber mats as a breathable barrier textile material. Text. Res. J. 2011, 82, 70–76. [Google Scholar] [CrossRef]
- Li, N.W.; Yick, K.L.; Yu, A. Novel weft-knitted spacer structure with silicone tube and foam inlays for cushioning insoles. J. Ind. Text. 2022. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, P. Compression fatigue resistance of three-dimensional warp-knitted spacer structure for car cushion. Fibers Polym. 2017, 18, 605–610. [Google Scholar] [CrossRef]
- Lo, W.T.; Yick, K.L.; Ng, S.P.; Yip, J. New methods for evaluating physical and thermal comfort properties of orthotic materials used in insoles for patients with diabetes. J. Rehabil. Res. Dev. 2014, 51, 311–324. [Google Scholar] [CrossRef] [PubMed]
- Erdumlu, N.; Saricam, C. Investigating the effect of some fabric parameters on the thermal comfort properties of flat knitted acrylic fabrics for winter wear. Text. Res. J. 2017, 87, 1349–1359. [Google Scholar] [CrossRef]
















| Factor | Level | |||
|---|---|---|---|---|
| Inlay density (ratio of spacer and inlay structure) | 4:1 | 3:2 | 1:1 | 2:3 |
| Inlay Orientation | Random | Localized | ||
| Number of spacer yarn per spacer structure | 1 course | 2 courses |
| pslp | Knitted Structure | Inlay Density (Course per cm) | Orientation of Inlay | Spacer Yarn Density (Course per cm) |
|---|---|---|---|---|
| AS1 | A | 1.20 | Random | 5 |
| AS2 | B | 1.20 | Random | 10 |
| BC1 | C | 2.00 | Localized | 5 |
| BC2 | D | 2.00 | Localized | 10 |
| BS1 | E | 2.00 | Random | 5 |
| BS2 | F | 2.00 | Random | 10 |
| CS1 | G | 2.30 | Random | 4 |
| CS2 | H | 2.30 | Random | 8 |
| DC2 | I | 2.50 | Localized | 10 |
| DS2 | J | 2.50 | Random | 10 |
| C1 | C1 | Nil | Nil | 13 |
| C2 | C2 | Nil | Nil | 26 |
| Fabric | AS1 | AS2 | BC1 | BC2 | BS1 | BS2 | CS1 | CS2 | DC2 | DS2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Structure | A | B | C | D | E | F | G | H | I | J |
| Knitting notation |  |  |  |  |  |  |  |  |  |  |
| Image |  |  |  |  |  |  |  |  |  |  |
| Property | Device | Testing Standard |
|---|---|---|
| Thickness | Dial thickness gauge (Model H, Peacock OZAKI MFG. Co., Ltd., Tokyo, Japan) | ASTM D1777 Standard Test Method for Thickness of Textile Materials |
| Hardness | Durometer (GS-744G, Type: FO, TECLOCK Co., Ltd., Nagano, Japan) | ASTM D2240-05: 2010 Standard Test Method for Rubber Property—Durometer Hardness |
| Surface unevenness | 3D-optical microscope (VR-3000, KEYENCE, Osaka, Japan) | ISO4287:1997 Surface unevenness-Definitions |
| Air permeability | Air permeability tester (SDL M021S, SDL International Textile Testing Solutions, Rock Hill, SC, USA) | ASTM-D737 Standard Test Method for Air Permeability of Textile Fabrics |
| Compression | Compression tester (Instron 4411, Instron, Norwood, MA, USA) | ASTM D575 Standard Test Methods for Rubber Properties in Compression |
| Thermal and evaporative resistance | Sweating guarded hot plate (YG(B)606G, Wenzhou, China) | ASTM F1868-17 Standard Test Method for thermal and evaporative resistance of clothing materials |
| Sample Code | Weight (g/m2) | Thickness (mm) | Stitch Density (loop/cm2) | Hardness (Shore A) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| AS1 | 1483.32 | 6.12 | 4.30 | 0.03 | 93.33 | 4.04 | 83.17 | 1.33 |
| AS2 | 1417.25 | 0.46 | 4.31 | 0.03 | 91.00 | 0.00 | 86.17 | 1.72 |
| BC1 | 1649.50 | 18.62 | 4.34 | 0.03 | 93.33 | 4.04 | 86.17 | 0.93 |
| BC2 | 1683.28 | 15.94 | 4.39 | 0.05 | 91.00 | 0.00 | 86.50 | 1.22 |
| BS1 | 1669.15 | 6.38 | 4.40 | 0.04 | 91.00 | 0.00 | 87.33 | 0.82 |
| BS2 | 1620.13 | 21.14 | 4.39 | 0.05 | 86.50 | 3.91 | 87.67 | 0.82 |
| CS1 | 1759.97 | 17.31 | 4.35 | 0.04 | 88.83 | 3.75 | 88.67 | 1.21 |
| CS2 | 1689.88 | 17.47 | 4.39 | 0.03 | 86.33 | 4.04 | 88.83 | 0.41 |
| DC2 | 1866.20 | 7.60 | 4.34 | 0.05 | 82.33 | 3.75 | 88.92 | 0.92 |
| DS2 | 1861.70 | 22.59 | 4.33 | 0.04 | 82.33 | 3.75 | 89.00 | 0.84 |
| C1 | 1094.38 | 5.65 | 3.51 | 0.05 | 108.00 | 4.00 | 88.67 | 1.37 |
| C2 | 1068.20 | 16.54 | 3.75 | 0.14 | 106.67 | 4.62 | 89.00 | 0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.-W.; Yick, K.-L.; Yu, A.; Ning, S. Mechanical and Thermal Behaviours of Weft-Knitted Spacer Fabric Structure with Inlays for Insole Applications. Polymers 2022, 14, 619. https://doi.org/10.3390/polym14030619
Li N-W, Yick K-L, Yu A, Ning S. Mechanical and Thermal Behaviours of Weft-Knitted Spacer Fabric Structure with Inlays for Insole Applications. Polymers. 2022; 14(3):619. https://doi.org/10.3390/polym14030619
Chicago/Turabian StyleLi, Nga-Wun, Kit-Lun Yick, Annie Yu, and Sen Ning. 2022. "Mechanical and Thermal Behaviours of Weft-Knitted Spacer Fabric Structure with Inlays for Insole Applications" Polymers 14, no. 3: 619. https://doi.org/10.3390/polym14030619
APA StyleLi, N. -W., Yick, K. -L., Yu, A., & Ning, S. (2022). Mechanical and Thermal Behaviours of Weft-Knitted Spacer Fabric Structure with Inlays for Insole Applications. Polymers, 14(3), 619. https://doi.org/10.3390/polym14030619