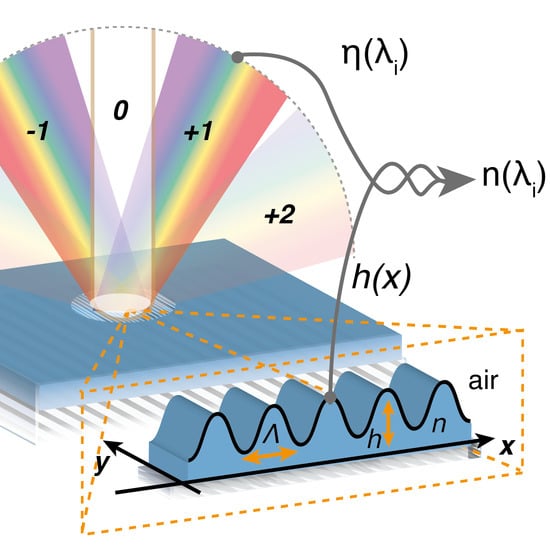
Diffractive Refractometer Based on Scalar Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Grating Fabrication
2.2. Diffraction Efficiency Measurement
2.3. AFM Characterization
3. Results
3.1. Refractive Index in the Scalar Diffraction Theory of Phase Gratings
3.2. Workflow of the Method
3.3. Measurement of the Refractive Index of PMMA
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eugene Hecht. Optics, 4th ed.; Addison-Wesley: San Francisco, CA, USA, 2002; ISBN 0-321-18878-0. [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; Wiley Series in Pure and Applied Optics; John Wiley & Sons, Inc.: New York, NY, USA, 1991; ISBN 978-0-471-83965-1. [Google Scholar]
- Lalanne, P.; Chavel, P. Metalenses at Visible Wavelengths: Past, Present, Perspectives. Laser Photonics Rev. 2017, 11, 1600295. [Google Scholar] [CrossRef]
- Banerji, S.; Meem, M.; Majumder, A.; Vasquez, F.G.; Sensale-Rodriguez, B.; Menon, R. Imaging with Flat Optics: Metalenses or Diffractive Lenses? Optica 2019, 6, 805. [Google Scholar] [CrossRef]
- Chen, W.T.; Capasso, F. Will Flat Optics Appear in Everyday Life Anytime Soon? Appl. Phys. Lett. 2021, 118, 100503. [Google Scholar] [CrossRef]
- Tearney, G.J.; Brezinski, M.E.; Southern, J.F.; Bouma, B.E.; Hee, M.R.; Fujimoto, J.G. Determination of the Refractive Index of Highly Scattering Human Tissue by Optical Coherence Tomography. Opt. Lett. OL 1995, 20, 2258–2260. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.-A.; Lim, H.-J.; Su, C.B. A Fibre Optic Fresnel Ratio Meter for Measurements of Solute Concentration and Refractive Index Change in Fluids. Meas. Sci. Technol. 2002, 13, 1962. [Google Scholar] [CrossRef]
- Tompkins, H.G.; Irene, E.A. Handbook of Ellipsometry; William Andrew Publishing: Norwich, UK, 2005; ISBN 978-0-8155-1499-2. [Google Scholar]
- Fujiwara, H.; Collins, R.W. (Eds.) Spectroscopic Ellipsometry for Photovoltaics: Volume 1: Fundamental Principles and Solar Cell Characterization; Springer Series in Optical Sciences; Springer International Publishing: Cham, Switzerland, 2018; Volume 212, ISBN 978-3-319-75375-1. [Google Scholar]
- Rheims, J.; Köser, J.; Wriedt, T. Refractive-Index Measurements in the near-IR Using an Abbe Refractometer. Meas. Sci. Technol. 1997, 8, 601. [Google Scholar] [CrossRef]
- Kachiraju, S.R.; Gregory, D.A. Determining the Refractive Index of Liquids Using a Modified Michelson Interferometer. Opt. Laser Technol. 2012, 44, 2361–2365. [Google Scholar] [CrossRef]
- Kim, C.-B.; Su, C.B. Measurement of the Refractive Index of Liquids at 1.3 and 1.5 Micron Using a Fibre Optic Fresnel Ratio Meter. Meas. Sci. Technol. 2004, 15, 1683. [Google Scholar] [CrossRef]
- Zhang, X.U.; Faber, D.J.; Post, A.L.; van Leeuwen, T.G.; Sterenborg, H.J.C.M. Refractive Index Measurement Using Single Fiber Reflectance Spectroscopy. J. Biophotonics 2019, 12, e201900019. [Google Scholar] [CrossRef]
- An, N.; Zhuang, B.; Li, M.; Lu, Y.; Wang, Z.-G. Combined Theoretical and Experimental Study of Refractive Indices of Water–Acetonitrile–Salt Systems. J. Phys. Chem. B 2015, 119, 10701–10709. [Google Scholar] [CrossRef]
- Li, M.; Zhuang, B.; Lu, Y.; Wang, Z.-G.; An, L. Accurate Determination of Ion Polarizabilities in Aqueous Solutions. J. Phys. Chem. B 2017, 121, 6416–6424. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, E.A.; Dib, L.F.G. Diffractive Refractometer for Liquid Characterization and Transient Processes Monitoring. Rev. Sci. Instrum. 2017, 88, 073103. [Google Scholar] [CrossRef]
- Calixto, S.; Piazza, V.; Gonzalez-Suarez, A.M.; Garcia-Cordero, J.L.; Bruce, N.C.; Rosete-Aguilar, M.; Garnica, G. Liquid Refractive Index Measured through a Refractometer Based on Diffraction Gratings. Opt. Express OE 2019, 27, 34705–34720. [Google Scholar] [CrossRef] [PubMed]
- Martelli, C.; Canning, J.; Kristensen, M.; Groothoff, N. Refractive Index Measurement within a Photonic Crystal Fibre Based on Short Wavelength Diffraction. Sensors 2007, 7, 2492–2498. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Whitesides, G.M. Soft Lithography. Angew. Chem. Int. Ed. 1998, 37, 550–575. [Google Scholar] [CrossRef]
- Liu, B.; Wang, M.; He, Y.; Wang, X. Duplication of Photoinduced Azo Polymer Surface-Relief Gratings through a Soft Lithographic Approach. Langmuir 2006, 22, 7405–7410. [Google Scholar] [CrossRef] [PubMed]
- Na, S.-I.; Kim, S.-S.; Jo, J.; Oh, S.-H.; Kim, J.; Kim, D.-Y. Efficient Polymer Solar Cells with Surface Relief Gratings Fabricated by Simple Soft Lithography. Adv. Funct. Mater. 2008, 18, 3956–3963. [Google Scholar] [CrossRef]
- Loewen, E.G.; Popov, E. Diffraction Gratings and Applications; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-21484-9. [Google Scholar]
- Popov, E.K.; Tsonev, L.V.; Loewen, E.G. Scalar Theory of Transmission Relief Gratings. Opt. Commun. 1991, 80, 307–311. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005; ISBN 978-0-9747077-2-3. [Google Scholar]
- Harvey, J.E.; Krywonos, A.; Bogunovic, D. Nonparaxial Scalar Treatment of Sinusoidal Phase Gratings. J. Opt. Soc. Am. A JOSAA 2006, 23, 858–865. [Google Scholar] [CrossRef]
- Andries, I.; Galstian, T.; Chirita, A. Approximate Analysis of the Diffraction Efficiency of Transmission Phase Holographic Gratings with Smooth Non-Sinusoidal Relief. J. Optoelectron. Adv. Mater. 2016, 18, 56–64. [Google Scholar]
- O’Shea, D.C.; Suleski, T.J.; Kathman, A.D.; Prather, D.W. Diffractive Optics; SPIE: Bellingham, WA, USA, 2003; ISBN 978-0-8194-5171-2. [Google Scholar]
- Reda, F.; Salvatore, M.; Borbone, F.; Maddalena, P.; Oscurato, S.L. Accurate Morphology-Related Diffraction Behavior of Light-Induced Surface Relief Gratings on Azopolymers. ACS Mater. Lett. 2022, 4, 953–959. [Google Scholar] [CrossRef]
- Harvey, J.E.; Pfisterer, R.N. Understanding Diffraction Grating Behavior: Including Conical Diffraction and Rayleigh Anomalies from Transmission Gratings. OE 2019, 58, 087105. [Google Scholar] [CrossRef]
- Harvey, J.E.; Pfisterer, R.N. Understanding Diffraction Grating Behavior, Part II: Parametric Diffraction Efficiency of Sinusoidal Reflection (Holographic) Gratings. OE 2020, 59, 017103. [Google Scholar] [CrossRef]
- Oscurato, S.L.; Salvatore, M.; Maddalena, P.; Ambrosio, A. From Nanoscopic to Macroscopic Photo-Driven Motion in Azobenzene-Containing Materials. Nanophotonics 2018, 7, 1387–1422. [Google Scholar] [CrossRef]
- Priimagi, A.; Shevchenko, A. Azopolymer-Based Micro- and Nanopatterning for Photonic Applications. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 163–182. [Google Scholar] [CrossRef]
- Natansohn, A.; Rochon, P. Photoinduced Motions in Azo-Containing Polymers. Chem. Rev. 2002, 102, 4139–4176. [Google Scholar] [CrossRef]
- Jelken, J.; Santer, S. Light Induced Reversible Structuring of Photosensitive Polymer Films. RSC Adv. 2019, 9, 20295–20305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Loebner, S.; Yadav, B.; Lomadze, N.; Tverdokhleb, N.; Donner, H.; Saphiannikova, M.; Santer, S. Local Direction of Optomechanical Stress in Azobenzene Containing Polymers During Surface Relief Grating Formation. Macromol. Mater. Eng. 2022, 307, 2100990. [Google Scholar] [CrossRef]
- Lim, Y.; Kang, B.; Lee, S. Photo-Transformable Gratings for Augmented Reality. Adv. Funct. Mater. 2021, 31, 2100839. [Google Scholar] [CrossRef]
- Rekola, H.; Berdin, A.; Fedele, C.; Virkki, M.; Priimagi, A. Digital Holographic Microscopy for Real-Time Observation of Surface-Relief Grating Formation on Azobenzene-Containing Films. Sci. Rep. 2020, 10, 19642. [Google Scholar] [CrossRef]
- Lim, Y.; Kang, B.; Hong, S.J.; Son, H.; Im, E.; Bang, J.; Lee, S. A Field Guide to Azopolymeric Optical Fourier Surfaces and Augmented Reality. Adv. Funct. Mater. 2021, 31, 2104105. [Google Scholar] [CrossRef]
- Audia, B.; Pagliusi, P.; Mazzulla, A.; Cipparrone, G. Multi-Wavelength Optical Patterning for Multiscale Materials Design. Photonics 2021, 8, 481. [Google Scholar] [CrossRef]
- Pagliusi, P.; Audia, B.; Provenzano, C.; Piñol, M.; Oriol, L.; Cipparrone, G. Tunable Surface Patterning of Azopolymer by Vectorial Holography: The Role of Photoanisotropies in the Driving Force. ACS Appl. Mater. Interfaces 2019, 11, 34471–34477. [Google Scholar] [CrossRef] [PubMed]
- Oscurato, S.L.; Reda, F.; Salvatore, M.; Borbone, F.; Maddalena, P.; Ambrosio, A. Shapeshifting Diffractive Optical Devices. Laser Photonics Rev. 2022, 2100514. [Google Scholar] [CrossRef]
- Strobelt, J.; Stolz, D.; Leven, M.; Soelen, M.V.; Kurlandski, L.; Abourahma, H.; McGee, D.J. Optical Microstructure Fabrication Using Structured Polarized Illumination. Opt. Express OE 2022, 30, 7308–7318. [Google Scholar] [CrossRef]
- Strobelt, J.; Van Soelen, M.; Abourahma, H.; McGee, D.J. Supramolecular Azopolymers for Dynamic Surface Microstructures Using Digital Polarization Optics. Adv. Opt. Mater. 2023, 2202245. [Google Scholar] [CrossRef]
- Sultanova, N.; Kasarova, S.; Nikolov, I. Dispersion Properties of Optical Polymers. Acta Phys. Pol. A 2009, 116, 585–587. [Google Scholar] [CrossRef]
- Beadie, G.; Brindza, M.; Flynn, R.A.; Rosenberg, A.; Shirk, J.S. Refractive Index Measurements of Poly(Methyl Methacrylate) (PMMA) from 0.4–1.6 Μm. Appl. Opt. AO 2015, 54, F139–F143. [Google Scholar] [CrossRef]
- Oscurato, S.L.; Borbone, F.; Maddalena, P.; Ambrosio, A. Light-Driven Wettability Tailoring of Azopolymer Surfaces with Reconfigured Three-Dimensional Posts. ACS Appl. Mater. Interfaces 2017, 9, 30133–30142. [Google Scholar] [CrossRef] [Green Version]
- Salvatore, M.; Borbone, F.; Oscurato, S.L. Deterministic Realization of Quasicrystal Surface Relief Gratings on Thin Azopolymer Films. Adv. Mater. Interfaces 2020, 7, 1902118. [Google Scholar] [CrossRef]
- Oscurato, S.L.; Reda, F.; Salvatore, M.; Borbone, F.; Maddalena, P.; Ambrosio, A. Large-Scale Multiplexed Azopolymer Gratings with Engineered Diffraction Behavior. Adv. Mater. Interfaces 2021, 8, 2101375. [Google Scholar] [CrossRef]
- Reda, F.; Salvatore, M.; Borbone, F.; Maddalena, P.; Ambrosio, A.; Oscurato, S.L. Varifocal Diffractive Lenses for Multi-Depth Microscope Imaging. Opt. Express OE 2022, 30, 12695–12711. [Google Scholar] [CrossRef] [PubMed]
- DeVore, J.R. Refractive Indices of Rutile and Sphalerite. J. Opt. Soc. Am. JOSA 1951, 41, 416–419. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salvatore, M.; Reda, F.; Borbone, F.; Januariyasa, I.K.; Maddalena, P.; Oscurato, S.L. Diffractive Refractometer Based on Scalar Theory. Polymers 2023, 15, 1605. https://doi.org/10.3390/polym15071605
Salvatore M, Reda F, Borbone F, Januariyasa IK, Maddalena P, Oscurato SL. Diffractive Refractometer Based on Scalar Theory. Polymers. 2023; 15(7):1605. https://doi.org/10.3390/polym15071605
Chicago/Turabian StyleSalvatore, Marcella, Francesco Reda, Fabio Borbone, I Komang Januariyasa, Pasqualino Maddalena, and Stefano Luigi Oscurato. 2023. "Diffractive Refractometer Based on Scalar Theory" Polymers 15, no. 7: 1605. https://doi.org/10.3390/polym15071605
APA StyleSalvatore, M., Reda, F., Borbone, F., Januariyasa, I. K., Maddalena, P., & Oscurato, S. L. (2023). Diffractive Refractometer Based on Scalar Theory. Polymers, 15(7), 1605. https://doi.org/10.3390/polym15071605