Effect of Carbon Nanofiber Distribution on Mechanical Properties of Injection-Molded Aramid-Fiber-Reinforced Polypropylene
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Melt-Blending
2.3. Injection Molding
2.4. Three-Point Bending Test
2.5. Uniaxial Tensile Test
2.6. Short-Beam Shear Test
2.7. Notched Charpy Impact Test
2.8. X-ray CT Imaging
2.9. Fracture Surface Observation
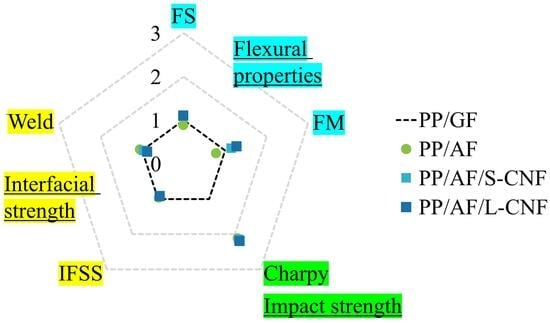
3. Results
3.1. Flexural Properties
3.2. Interfacial Mechanical Properties
3.3. Notched Charpy Impact Strength
4. Discussions
4.1. Carbon Nanofiber Dispersion Effects on Notched Impact Strength of PP/AF Composites
4.2. Carbon Nanofiber Dispersion Effects on Flexural Properties of PP/AF Composites
5. Conclusions
- CNF dispersion in PP/AF improved the flexural strength and flexural modulus without compromising impact resistance. Depending on the CNF content, these values were higher than those of glass-fiber-reinforced injection-molded polypropylene products.
- Interfacial mechanical properties were slightly decreased by dispersing CNF in PP/AF. This improvement was attributed to the change in interfacial interaction forces caused by the CNF dispersion.
- The skin layer of PP/AF injection-molded products showed a tendency for fiber orientation to be parallel to the flow direction due to CNF dispersion, while the core layer’s fiber orientation remained unchanged.
- The impact strength of PP/AF injection-molded products is not dependent on CNF content, which can be explained by changes in AF volume content and IFSS, as predicted by the fiber pull-out model.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, S.-S.; Jin, F.-L.; Rhee, K.Y.; Hui, D.; Park, S.-J. Recent advances in carbon-fiber-reinforced thermoplastic composites: A review. Compos. Part B Eng. 2018, 142, 241–250. [Google Scholar] [CrossRef]
- Unterweger, C.; Brüggemann, O.; Fürst, C. Synthetic fibers and thermoplastic short-fiber-reinforced polymers: Properties and characterization. Polym. Compos. 2014, 35, 227–236. [Google Scholar] [CrossRef]
- Wan, Y.; Takahashi, J. Development of Carbon Fiber-Reinforced Thermoplastics for Mass-Produced Automotive Applications in Japan. J. Compos. Sci. 2021, 5, 86. [Google Scholar] [CrossRef]
- Jagadeesh, P.; Mavinkere Rangappa, S.; Siengchin, S.; Puttegowda, M.; Thiagamani, S.M.K.; Rajeshkumar, G.; Kumar, M.H.; Oladijo, O.P.; Fiore, V.; Moure Cuadrado, M.M. Sustainable recycling technologies for thermoplastic polymers and their composites: A review of the state of the art. Polym. Compos. 2022, 43, 5831–5862. [Google Scholar] [CrossRef]
- Cabrera, G.; Li, J.; Maazouz, A.; Lamnawar, K. A Journey from Processing to Recycling of Multilayer Waste Films: A Review of Main Challenges and Prospects. Polymers 2022, 14, 2319. [Google Scholar] [CrossRef] [PubMed]
- Yasir Khalid, M.; Ullah Arif, Z.; Ahmed, W.; Arshad, H. Recent trends in recycling and reusing techniques of different plastic polymers and their composite materials. Sustain. Mater. Technol. 2022, 31, e00382. [Google Scholar]
- Ghosh, A. Performance modifying techniques for recycled thermoplastics. Resour. Conserv. Recycl. 2021, 175, 105887. [Google Scholar] [CrossRef]
- Ben, G.; Hirabayashi, A.; Sakata, K.; Nakamura, K.; Hirayama, N. Evaluation of new GFRTP and CFRTP using epsilon caprolactam as matrix fabricated with VaRTM. Sci. Eng. Compos. Mater. 2015, 22, 633–641. [Google Scholar] [CrossRef]
- Almushaikeh, A.M.; Alaswad, S.O.; Alsuhybani, M.S.; Alotaibi, B.M.; Alarifi, I.M.; Alqahtani, N.B.; Aldosari, S.M.; Alsaleh, S.S.; Haidyrah, A.S.; Alolyan, A.A.; et al. Manufacturing of carbon fiber reinforced thermoplastics and its recovery of carbon fiber: A review. Polym. Test. 2023, 122, 108029. [Google Scholar] [CrossRef]
- Kang, B.; Kim, D.; Sohn, J.S.; Park, N.; Kim, K.; Kim, H.J.; Youngdeog, K.; Choi, B.H. Observations of Short-and Long-Term Mechanical Properties of Glass Fiber Reinforced Polypropylenes with Post-Consumer Recycled Materials. Int. J. Precis. Eng. Manuf. Green Technol. 2024, 11, 523–535. [Google Scholar]
- Chen, T.; Mansfield, C.D.; Ju, L.; Baird, D.G. The influence of mechanical recycling on the properties of thermotropic liquid crystalline polymer and long glass fiber reinforced polypropylene. Compos. Part B 2020, 200, 108316. [Google Scholar] [CrossRef]
- Yang, G.; Park, M.; Park, S.-J. Recent progresses of fabrication and characterization of fibers-reinforced composites: A review. Compos. Commun. 2019, 14, 34–42. [Google Scholar] [CrossRef]
- Zhang, B.; Jia, L.; Tian, M.; Ning, N.; Zhang, L.; Wang, W. Surface and interface modification of aramid fiber and its reinforcement for polymer composites: A review. Eur. Polym. J. 2021, 147, 110352. [Google Scholar] [CrossRef]
- Azizi Samir, M.A.S.; Alloin, F.; Dufresne, A. Review of recent research into cellulosic whiskers, their properties and their application in nanocomposite field. Biomacromolecules 2005, 6, 612–626. [Google Scholar] [CrossRef] [PubMed]
- Roeder, R.K.; Sproul, M.M.; Turner, C.H. Hydroxyapatite whiskers provide improved mechanical properties in reinforced polymer composites. J. Biomed. Mater. Res. A 2003, 67, 801–812. [Google Scholar] [CrossRef] [PubMed]
- ISO 178:2019; Plastics−Determination of Flexural Properties. The British Standards Institution: London, UK, 2019.
- ISO 527-2:2012; Tensile Testing for Plastics. The British Standards Institution: London, UK, 2012.
- Jiang, Q.; Takayama, T.; Nishioka, A. Improving the Accuracy of the Evaluation Method for Interfacial Shear Strength of FRTP through Short Beam Shear Test. Polymers 2024, 16, 883. [Google Scholar] [CrossRef] [PubMed]
- ISO 179-1:2023; Plastics-Determination of Charpy Impact Properties-Part 1: Non-Instrumented Impact Test. The British Standards Institution: London, UK, 2023.
- Jiang, Q.; Takayama, T.; Nishioka, A. Impact Energy Dissipation Quantitative Models of Injection Molded Short Fiber Reinforced Thermoplastics. Polymers 2023, 15, 4297. [Google Scholar] [CrossRef] [PubMed]
- Aliotta, L.; Lazzeri, A. A proposal to modify the Kelly-Tyson equation to calculate the interfacial shear strength (IFSS) of composites with low aspect ratio fibers. Compos. Sci. Technol. 2020, 186, 107920. [Google Scholar] [CrossRef]
- Omidi, M.; Rokni, D.T.H.; Milani, A.S.; Seethaler, R.J.; Arasteh, R. Prediction of the mechanical characteristics of multi-walled carbon nanotube/epoxy composites using a new form of the rule of mixtures. Carbon 2010, 48, 3218–3228. [Google Scholar] [CrossRef]
- Takayama, T.; Motoyama, Y. Injection molding temperature dependence of elastic coefficients obtained using three-point bending tests to ascertain thermoplastic polymer coefficients. Mech. Eng. J. 2021, 8, 20–414. [Google Scholar] [CrossRef]
- Takayama, T. Weld strength of injection molded short fiber reinforced polypropylene. Mech. Mater. 2019, 136, 103064. [Google Scholar] [CrossRef]

















| Material | Code | Manufacturer | Name | Density [g/cm3] |
|---|---|---|---|---|
| Poly propylene | PP | Japan Polypropylene Corp. Tokyo, Japan | Novatec-PP MA1B | 0.91 |
| Aramid Fiber | AF | Teijin Co., Ltd. Tokyo, Japan | Technora ZCF1-12 | 1.4 |
| Glass Fiber | GF | Nippon Electric Glass Co., Ltd. Shiga, Japan | ECS 03 T-351 | 2.56 |
| Carbon Nano Fiber | S-CNF | Almedio Co., Ltd. Tokyo, Japan | Carbon nanofiber for reinforcement | 2.2 |
| L-CNF | Almedio Co., Ltd. Tokyo, Japan | Carbon nanofiber for electrical conductivity | 2.2 |
| PP [wt%] | GF [wt%] | AF [wt%] | S-CNF [wt%] | L-CNF [wt%] | Tinj [°C] | Tmold [°C] | Vinj [m/s] | Phold [MPa] | tinj [s] | tcool [s] |
|---|---|---|---|---|---|---|---|---|---|---|
| 90 | 10 | - | - | - | 230 | 50 | 10 | 53 | 30 | 15 |
| 90 | - | 10 | - | - | 230 | 50 | 30 | 56 | 10 | 15 |
| 89 | - | 10 | 1 | - | 230 | 50 | 30 | 53 | 10 | 15 |
| 87 | - | 10 | 3 | - | 230 | 50 | 30 | 60 | 10 | 15 |
| 85 | - | 10 | 5 | - | 230 | 50 | 30 | 63 | 10 | 15 |
| 89 | - | 10 | - | 1 | 230 | 50 | 30 | 56 | 10 | 15 |
| 87 | - | 10 | - | 3 | 230 | 50 | 30 | 60 | 10 | 15 |
| 85 | - | 10 | - | 5 | 230 | 50 | 30 | 63 | 10 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takayama, T.; Kobayashi, S.; Yuasa, Y.; Jiang, Q. Effect of Carbon Nanofiber Distribution on Mechanical Properties of Injection-Molded Aramid-Fiber-Reinforced Polypropylene. Polymers 2024, 16, 1110. https://doi.org/10.3390/polym16081110
Takayama T, Kobayashi S, Yuasa Y, Jiang Q. Effect of Carbon Nanofiber Distribution on Mechanical Properties of Injection-Molded Aramid-Fiber-Reinforced Polypropylene. Polymers. 2024; 16(8):1110. https://doi.org/10.3390/polym16081110
Chicago/Turabian StyleTakayama, Tetsuo, Shunsuke Kobayashi, Yuuki Yuasa, and Quan Jiang. 2024. "Effect of Carbon Nanofiber Distribution on Mechanical Properties of Injection-Molded Aramid-Fiber-Reinforced Polypropylene" Polymers 16, no. 8: 1110. https://doi.org/10.3390/polym16081110
APA StyleTakayama, T., Kobayashi, S., Yuasa, Y., & Jiang, Q. (2024). Effect of Carbon Nanofiber Distribution on Mechanical Properties of Injection-Molded Aramid-Fiber-Reinforced Polypropylene. Polymers, 16(8), 1110. https://doi.org/10.3390/polym16081110