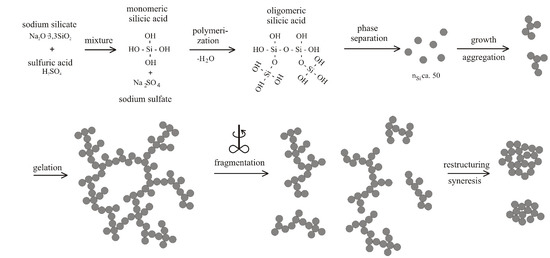
4.1. Natural Syneresis
The time-dependent development of the volume decrease Δ
V/
V0 for three different temperatures is presented in
Figure 6. Each symbol represents the averaged value of three measured gel samples. The scale of the
Y-axis is inverted, so that gel samples with smaller volumes (
i.e., higher values for a volume decrease Δ
V/
V0) are shown in the lower part of the diagram. This figure can be split into two sections, independent of temperature. The first section is for
t ≤ 50 h and the second one for
t > 50 h. In the first section, the gel shrinks quickly, because it remains flexible due to uncondensed hydroxyl groups. With time, these uncondensed groups polymerize, causing a continuously stiffening solid skeleton that can resist further shrinkage. This is expressed in a rate reduction of volume decrease Δ
V/
V0 in the second section. For longer times, the volume decrease approaches a maximum value (Δ
V/
V0)
max asymptotically. An increase in temperature leads to faster shrinkage of the gel, because of a higher movement of the pore liquid through the gel network and a higher polymerization rate. By contrast, the total amount of shrinkage remains unchanged. This is contrary to the phenomenon of a slightly smaller volume decrease with increasing temperature, determined by [
10]. When regarding the error bars plotted in
Figure 6, this statement can be neither proven nor disproven.
Figure 6.
Volume decrease for different temperatures, natural syneresis.
Figure 6.
Volume decrease for different temperatures, natural syneresis.
For the description of the course of volume decrease with time and its maximum value at
t→∞ by means of a mathematical model, each curve may be fitted via an empirical model that is based upon a kinetic rate equation:
while the first fit parameter (Δ
V/
V0)
max accounts for the maximum volume decrease, the second parameter τ represents a characteristic time constant affecting the rate of volume decrease. An exponent
n is added to ensure a good agreement between the measured and modeled rates.
Table 1 lists the values of these fitting parameters.
Table 1.
Fitting parameters and fitting errors of the empirical equation for natural syneresis.
Table 1.
Fitting parameters and fitting errors of the empirical equation for natural syneresis.
| Temperature ϑ/°C | Maximum Volume Decrease (ΔV/V0)max | Time Constant τ/h | Exponent n | Fitting Error R2 |
|---|
| 20 | 0.197 | 21.7 | 1.23 | 0.868 |
| 40 | 0.197 | 11.1 | 1.23 | 0.867 |
| 60 | 0.198 | 5.6 | 1.23 | 0.988 |
The curves of the empirical model are shown in
Figure 6. A higher temperature leads to a reduced time constant τ. It turns out that the exponent
n varies between 1.21 and 1.25, depending on the temperature. In order to minimize the number of fitting parameters, a constant value of 1.23 is chosen without changing the residuum sum of squares to any appreciable extent. Even in the case of
n = 1, the measured rates are reproduced correctly within the error bars, but with a larger residuum sum of squares compared to
n = 1.23. We have decided to use
n = 1.23 in order to compare the rates at different temperatures.
4.2. Enforced Syneresis
Natural syneresis is a slow and time-consuming shrinkage process; see the previous section. With enforced syneresis, investigations can be made in a significantly shorter time. In
Figure 7, the volume decrease Δ
V/
V0 measured (solid line) is plotted for a constant temperature of ϑ = 20 °C as a function of time
t and the pressure difference Δ
p applied caused by the external force
F. As expected, higher pressure differences Δ
p result in faster gel shrinkage. Similarly, the maximum volume decrease (Δ
V/
V0)
max exhibits larger values. Each curve for the volume decrease Δ
V/
V0 measured is fitted using the same empirical model (Equation (1)), as already proposed for natural syneresis. The empirical model (dashed lines in
Figure 7) is in good accordance with the curves measured. There are small deviations merely for
t < 12 h and Δ
p = 0.8 bar, caused by the empirical model itself.
Figure 7.
Enforced syneresis for ϑ = 20 °C.
Figure 7.
Enforced syneresis for ϑ = 20 °C.
Table 2 lists the values of the fitting parameters (Δ
V/
V0)
max and τ, depending on the applied pressure difference Δ
p for a temperature of ϑ = 20 °C. For reasons of simplicity, the curves for Δ
p = 3.2 bar and Δ
p = 6.5 bar are not shown in
Figure 7. They lie between the curves of Δ
p = 2.4 bar and Δ
p = 4 bar, respectively Δ
p = 5 bar and Δ
p = 8 bar. All values reflect quantitatively the conclusion of a larger maximum volume decrease and faster shrinkage due to a larger pressure difference. As for the natural syneresis, we set the exponent
n to a constant value of 1.23.
Table 2.
Fitting parameters and fitting errors of the empirical equation for enforced syneresis, ϑ = 20 °C.
Table 2.
Fitting parameters and fitting errors of the empirical equation for enforced syneresis, ϑ = 20 °C.
| Pressure Difference Δp/bar | Maximum Volume Decrease (ΔV/V0)max | Time Constant τ/h | Exponent n | Fitting Error R2 |
|---|
| 0.8 | 0.53 | 13.0 | 1.23 | 0.983 |
| 1.6 | 0.63 | 8.4 | 1.23 | 0.999 |
| 2.4 | 0.69 | 5.9 | 1.23 | 0.997 |
| 3.2 | 0.71 | 4.1 | 1.23 | 0.996 |
| 4 | 0.73 | 3.5 | 1.23 | 0.996 |
| 5 | 0.77 | 2.3 | 1.23 | 0.998 |
| 6.5 | 0.79 | 2.0 | 1.23 | 0.998 |
| 8 | 0.80 | 1.5 | 1.23 | 0.997 |
| 15.5 | 0.87 | 1.1 | 1.23 | 0.994 |
The temperature dependency of enforced syneresis is investigated by raising the temperature to ϑ = 40 °C and ϑ = 60 °C.
Figure 8 shows the measurement results (solid lines). In direct comparison with
Figure 7, each curve of Δ
p is shifted to shorter times, but to negligibly different values for the maximum volume decrease (Δ
V/
V0)
max. A temperature change affects only the rate of volume decrease. Thus, enforced syneresis behaves in exactly the same way as natural syneresis with respect to temperature dependency.
Figure 8.
Enforced syneresis for ϑ = 40 °C and ϑ = 60 °C.
Figure 8.
Enforced syneresis for ϑ = 40 °C and ϑ = 60 °C.
The values for the fitting parameters of the empirical model confirm these results. They are listed in Table S1. An increased temperature results in smaller characteristic time constants τ, but the maximum volume decreases (ΔV/V0)max are unaffected.
4.3. Correlation between Natural and Enforced Syneresis
The method for a correlation between natural and enforced syneresis is based upon correlations for the maximum volume decrease (Δ
V/
V0)
max and for the characteristic time constant τ as a function of the pressure difference Δ
p and temperature ϑ. Firstly, this dependency for the maximum volume decrease (Δ
V/
V0)
max is modeled; see
Figure 9. Here, natural syneresis is in accordance with Δ
p = 0 bar, and the values measured are represented by the filled symbols. The blank symbols correspond to the values of enforced syneresis, listed in
Table 2 and Table S1. All of the measured points of enforced syneresis may be fitted with an equation of the form:
Table 3 lists the values of the fitting parameters for the three different temperatures of ϑ = 20, 40, 60 °C. The function reflects the progression of enforced syneresis sufficiently. Small deviations occur only for a pressure difference of Δ
p = 15.5 bar. These can be neglected, because the region of low pressure differences is more relevant for the correlation between natural and enforced syneresis.
Figure 9.
Maximum volume decrease (ΔV/V0)max as a function of pressure difference Δp.
Figure 9.
Maximum volume decrease (ΔV/V0)max as a function of pressure difference Δp.
Table 3.
Fitting parameters and fitting errors for maximum volume decrease (ΔV/V0)max.
Table 3.
Fitting parameters and fitting errors for maximum volume decrease (ΔV/V0)max.
| Temperature ϑ/°C | Parameter A | Parameter B/bar | Parameter C/bar | Fitting Error R2 |
|---|
| 20 | −0.14 | −0.72 | 0.57 | 0.979 |
| 40 | −0.14 | −0.81 | 0.57 | 0.992 |
| 60 | −0.18 | −0.61 | 0.57 | 0.965 |
In addition to the reflection of enforced syneresis, this model allows for extrapolation to natural syneresis (dotted lines shown in
Figure 9). Their logarithmic, extrapolated values correspond to
A +
B/
C (Δ
p = 0 bar in Equation (2)) and reach values of
,
and
with increasing temperature. Thus, the maximum volume decreases correspond to
,
and
. By comparison, we measured
independent of the temperature for natural syneresis. Thus, we are able to predict the maximum volume change qualitatively with a relative error of 25% in the case of ϑ = 20 °C. For ϑ = 60 °C, the error is about 45%. We assume that the errors can be minimized with experiments at even lower pressure differences than Δ
p = 0.8 bar.
In analogy to the approach for the maximum volume decrease (Δ
V/
V0)
max, the pressure difference dependency of the characteristic time constant τ is correlated. The graphical presentation in a log–log graph is appropriate due to the very different orders of magnitude for τ (0.2 h ≤ τ ≤ 22 h). For that purpose, the pressure difference Δ
p is unsuitable for the abscissa because of its zero-value for natural syneresis. To compensate for that, an artificial pressure
p* = 1 bar is added to the pressure difference Δ
p.
Figure 10 shows this diagram. Similar to the previous figure, the blank symbols represent the measured characteristic time constants τ for enforced syneresis, while the filled symbols mark the measured time constants for natural syneresis. They are listed in
Table 1,
Table 2 and Table S1.
A linear function of the form:
is used for the calculation of τ depending on the pressure difference Δ
p applied. The fitting parameter
D represents the extrapolated characteristic time constant τ for natural syneresis. Time constants of enforced syneresis are calculated using the slope
E and the pressure difference Δ
p.
Table 4 specifies these two parameters. Their graphical representations are given in
Figure 10 (solid, dashed and dotted line). Each linear equation reflects the values of τ determined for enforced syneresis. Natural syneresis is accounted for via an extrapolation to Δ
p = 0 bar,
i.e.,
D = log(τ
extra/h).
Figure 10.
Characteristic time constant τ as a function of pressure difference Δp.
Figure 10.
Characteristic time constant τ as a function of pressure difference Δp.
In comparison to the measurements (see
Table 1), the model overestimates the characteristic time constants. Their extrapolated values are τ
extra = 24.0 h, τ
extra = 13.8 h and τ
extra = 7.1 h for increasing temperature. Thus, the maximum relative error is 24%. As in the case of maximum volume decrease, we assume a minimization of this error through experimental results at lower pressure differences than Δ
p = 0.8 bar.
Through the combination of Equations (2) and (3), we developed a predictive model that permits the evaluation of both natural and enforced syneresis. In particular, the maximum volume decrease (Δ
V/
V0)
max and the characteristic time constant τ are calculated as a function of the pressure difference Δ
p applied for the process of syneresis. A comparison between the measured and predicted progress of enforced syneresis for ϑ = 20 °C is shown in
Figure 11.
Table 4.
Fitting parameters and fitting errors for characteristic time constant τ.
Table 4.
Fitting parameters and fitting errors for characteristic time constant τ.
| Temperature ϑ/°C | Parameter D | Parameter E | Fitting Error R2 |
|---|
| 20 | 1.38 | −1.20 | 0.965 |
| 40 | 1.14 | −1.31 | 0.986 |
| 60 | 0.85 | −1.31 | 0.971 |
Figure 11.
Comparison between measured and predicted progress of enforced syneresis for ϑ = 20 °C.
Figure 11.
Comparison between measured and predicted progress of enforced syneresis for ϑ = 20 °C.
There is good agreement between measured and predicted syneresis. Though, in the case of Δ
p = 0.8 bar and Δ
p = 2.4 bar, the prediction model underestimates minimally the maximum volume decrease (Δ
V/
V0)
max. This is due to the fit of the maximum volume decrease, as shown in
Figure 9. The characteristic time constant τ is calculated with adequate precision, resulting in negligible differences of the rate between measured and predicted syneresis. For the comparison at higher temperatures of ϑ = 40 and ϑ = 60 °C, we refer to Figure S1. The maximum volume decrease (Δ
V/
V0)
max calculated is in good accordance with the measured values, but the course of syneresis is not predicted correctly for every pressure difference Δ
p. This is due to the disagreement between measured and fitted data, shown in
Figure 10. In summary, the enforced syneresis, depending on temperature ϑ and on the pressure difference Δ
p, can be predicted with minor deviations.
In addition to the determination of enforced syneresis, the predictive model developed is used to calculate the process of natural syneresis with respect to the maximum volume decrease (Δ
V/
V0)
max and the rate (represented by τ). The comparison between measured and predicted natural syneresis is given in
Figure 12. The rate is predicted with good agreement with the measurements (represented by the blank symbols, already shown in
Figure 6). With increasing temperature ϑ, the predicted rate of syneresis increases. The maximum volume decrease (Δ
V/
V0)
max cannot be calculated correctly for all temperatures, as may have been already concluded from
Figure 9. The relative errors of 25% and 45% are caused by these deviations. This is expressed in the differences to the measured values of volume decrease for ϑ = 20 and ϑ = 60 °C. To compensate for that, more data in the important region of low pressure differences Δ
p are necessary.
Figure 12.
Comparison between measured and predicted progress of natural syneresis.
Figure 12.
Comparison between measured and predicted progress of natural syneresis.