Structure and Frictional Properties of Colloid Gel

Abstract

Polymer gels are known to be opaque when the preparation conditions, such as the reaction temperature and the composition, are changed. The increase of the opaqueness of the gel suggests strongly the change of network structure. Here, we are going to review the recent studies on the structure and the frictional study of the opaque poly(acrylamide) gel. The results indicate that the opaque poly(acrylamide) gel consists of the fractal aggregate of the colloidal particles of sub-micrometer in size. The density of the colloid particle is calculated from the structural parameters and is found to be of the order of about 1 g/cm³. The results indicate that the main chain component and the cross-linker is densely cross-linked into the particle. The frictional property of poly(acrylamide) gel is analyzed in terms of the structural parameters of the gel. It is found that the frictional property of the opaque gel is well explained in terms of the structural parameters of the opaque gel.

1. Introduction

Polymer gel is a state of soft matter that is created by the cross-linked polymer network and the huge amount of solvent. Because of this structure, the gel is soft and elastic and, hence, used in a wide variety of science and technology, such as separation technologies and food materials. Among others, poly(acrylamide) gel is one of the most frequently used synthetic polymer gels in electrophoresis, because of the clarity of the gel and the easiness in handling.

It has been reported that poly(acrylamide) gel becomes opaque when the concentration of the cross-linking agent is increased [1,2].

Figure 1 shows the appearance of poly(acrylamide) gels that are prepared at various concentrations of the cross-linker under constant total concentration of the gels. It is clear from the image that the opacity of the gels increases with the concentration of the cross-linker. Since the opacity of the gels is static, that is the opacity of the gels is independent of time, some large structure is frozen into the polymer network of the gels. This phenomenon itself was well known even more than forty years ago. Although several studies have been made, the details of the phenomenon, as well as the actual three-dimensional structure of the gel has not been clarified until recently.

Figure 1. The appearance of the opaque poly(acrylamide) gels. The mole fraction of the cross-linker is 0.01, 0.03, 0.05 and 0.1 from left to right. The total concentration of the pre-gel solution is fixed at 700 mM.

Figure 1. The appearance of the opaque poly(acrylamide) gels. The mole fraction of the cross-linker is 0.01, 0.03, 0.05 and 0.1 from left to right. The total concentration of the pre-gel solution is fixed at 700 mM.

Meanwhile, the understanding of the physics of gels has continued extensively after the discovery of the volume phase transition in gels [3]. It was eventually recognized that the friction between the polymer network of the gel and the solvent is a characteristic property of the gel, and it plays an essential role during the phase transition. Then, systematic studies of the frictional properties of the gels were made [4,5,6]. It is shown in these studies that the friction coefficient between the polymer network of the gel and the solvent is quite sensitive to the structure of the polymer network.

One can easily expect that the opacity of the gel is caused by the emergence of the density fluctuations within the gel, and then, it is frozen into the polymer network of the gel. The structure of the opaque gels and their transport properties have been also studied by several researchers [7,8]. The transport properties of the gels, however, have never been discussed in terms of the real-space structure of the gels. The main reason for this may be due to the fact that the structure of the gels is so complex, and hence, usual scattering techniques, such as X-ray, neutron and/or light, are helpless to solve the real-space structure of the gels. We, however, recognize that in the case of opaque gels, the optical microscope technique can be really useful to study the structure of the gels, because the typical length scale of the structure is the same order of magnitude as the wavelength of the light. In this review, therefore, we present the structural study of an opaque gel by using the confocal laser scanning microscope (CLSM) technique. Then, the frictional property of the opaque gel is discussed in terms of the resolved real-space structure of the gel [9,10,11].

2. Experimental Section

2.1. Materials

The sample gel used in the present experiments is poly(acrylamide) gel. Since this gel is frequently used in separation technologies, the procedure to prepare the gel is already well established. The samples of acrylamide (main constituent) and N,N′-methylene-bis-acrylamide (cross-linker) were obtained from BioRad Co. (Hercules, CA, USA) and used without further purification. The predetermined amounts of acrylamide and N,N′-methylene-bis-acrylamide are dissolved into pure water, which is prepared by a Milli-Q system (Millipore Japan, Tokyo, Japan). Then, the initiator is dissolved into the solution. The light-sensitive initiator, 2,2′-azobis[2-methylene-N-(2-hydroxyethyl)propionamide] (VA-086), which was kindly provided by Wako Chemical Co. (Osaka, Japan), is employed in this study. It is well known that the swelling of the gel becomes obvious if the polymer network of the gel contains the ionic groups according to the increase in the osmotic pressure of the dissociated ions. The swelling of the gel easily alters the structure of the gel, which is formed during the gelation reaction. The ionic groups are automatically introduced into the polymer network of the gel, as long as a conventional initiator system is used; ammoniumpersulfate and N,N,N′,N′-tetramethylethylenediamine. Such an alteration of the structure of the polymer network should be strictly avoided to obtain the accurate structural information of the gel. Therefore, we use the above initiator, VA-086, in this study. The initiator used here is completely non-ionic, and hence, the resultant gel becomes a nonionic gel. The pre-gel solution is de-gassed for about 30 min before transfer to the desired glass container, and then, UV light at a wavelength of 360 nm is shone upon it to initiate the reaction. Prior to the observation of the real-space structure of the gel by a confocal laser scanning microscope (CLSM), the gel is labeled by a fluorescence dye, fluorescein isothiocianate (FITC, Isomer I, SIGMA-ALDRICH, St. Louis, MI, USA), by a standard method.

2.2. Real-Space Structure of Gel

The CLSM system used here consists of the inverted microscope (Carl Zeiss, Axiovert S100, Jena, Germany), the confocal unit (Yokogawa Electric Co., CSU 10, Tokyo, Japan), the image processing apparatus (Hamamatsu Photonics, cooled charge coupled device camera (CCD camera), C5985H and control unit, Argus 20, Hamamatsu, Japan), and the Ar-ion laser (type 532-50BS/170, Omnichrome, 488 nm, 50 mW, Salt Lake City, UT, USA). The CLMS images obtained are analyzed by image processing software (Scanalytic Inc., IPLab Spectrum, Fairfax, VA, USA). The objective lenses used here are Plan-Apochromat (Carl Zeiss; magnification 100×; Numerical Aperture (N.A.), 1.4) and C-Apochromat (Carl Zeiss; magnification 40×; N.A., 1.2, and magnification 10×; N.A., 0.45). According to the manufacturer, the thickness of the focal plane in this system is 1 µm (100× and 40×) and 15 µm (10×). The images that are used to analyze the real-space structure of the gel are gained at a magnification of 100×, but other objective lenses are used if necessary to check the structure of the gel in the larger scale. Therefore, the thickness of the observed volume is chosen as 1 µm in the following calculations. The image that is captured by the CCDs camera consists of a number of cells, which are called pixels. The calibration of the pixel size in the image yields that the one side of the pixel corresponds to 90 nm in the real space at a magnification of 100×. In the present CLSM system, the fluorescence dye is excited by laser light at a wavelength of 488 nm, and then, the image of emitted fluorescence at a wavelength of 525 nm is captured. When the sample is observed by the CLSM, p-phenylenediamine solution, which is a fade prevention substance of the fluorescence dye, is added in the surrounding water. The concentration of the fade prevention substance is fixed at 0.1 g/100 mL.

The fluorescence light intensity of the background is inevitable, even in the case of the CLSM imaging. We, therefore, synthesized thinner gels of a thickness less than 70 µm in the case of the structural studies. The overall quality of the CLSM images is considerably improved in the case of such thinner gels. All the images shown here are, thus, presented without image enhancement.

2.3. Friction of Gel

The principle of the mechanical measurement of the friction coefficient of a gel is schematically illustrated in Figure 2. A slab of a gel of thickness L is kept in a capillary with the limb fixed to the glass wall. The water is pushed by small pressure, P. The velocity of the water flow through the gel, v, is determined by measuring the rate at which water flows out of the gel in a steady state. The friction coefficient of the gel, f, is defined as follows.

Figure 2. The schematic illustration of the friction measurement.

Figure 2. The schematic illustration of the friction measurement.

(1)

Equation (1) is one of the expressions of Darcy’s law for the fluid flow in a porous material. The frictional properties of the transparent poly(acrylamide) gel have been studied in detail. The previous studies indicate that careful experiments are required to obtain a reliable value of the friction coefficient of the transparent poly(acrylamide) gel, since the friction of the transparent gel is considerably huge. In the case of opaque gel, however, the friction is expected to be much smaller than the transparent gel, because of the presence of large-scale density fluctuations within the gel. We thus employ a simple apparatus, which is specially designed for this study. In Figure 3, we show the apparatus for the friction measurements used in this study schematically.

Figure 3. The setup for the friction measurements in the present study.

Figure 3. The setup for the friction measurements in the present study.

A capillary of about 0.5 mm in diameter, in which the gel is synthesized at the end portion, is immersed into a large amount of water at a desired depth, h₀. Then, the height of the water inside the capillary, h(t), is measured as a function of time. In this geometry, the hydrostatic pressure that is applied to the opened end of the gel is expressed as follows.

(2)

Here, ρ and g denote the density of water and the acceleration of gravity. The linear velocity of the fluid in the gel is then expressed as follows:

(3)

Substitution of Equations (2) and (3) into Equation (1) yields the following:

(4)

The time course of water flow through the gel is then written as follows:

(5)

where the characteristic time, τ, is given by the following equation.

(6)

Thus, the friction coefficient of the gel is determined from the elution time course of water through the gel. All of the apparatus is set on an optical table to avoid any mechanical disturbance. The height of the water in the capillary, h(t), as well as the initial depth of the water, h₀, are measured by the moving microscope. The typical value of the initial depth is about 5–7 cm. Prior to the friction measurement, the opened end of the gel is kept in contact with the water until the height of the water inside the capillary becomes constant. The effects of the pressure change due to the capillary force are thus minimized. The friction measurements are made at a temperature of 23 °C.

3. Results and Discussion

3.1. Real Space Structure of Opaque Gel

It is well known that most polymer gels are swollen or shrunken when they are left in a huge amount of solvent. This indicates that the volume change of the gel easily alters the network structure of the gel. We therefore firstly measured the swelling ratios of the opaque gels, which are prepared under various reaction conditions, in water in the equilibrium state. The results are shown in Figure 4.

It is clear from the results that the swelling ratios of the opaque gels are almost unity, that is, they do not swell and/or shrink under water. Therefore, the structure of the opaque gel that is created during the gel formation reaction is conserved, even though the gels are left in water.

Figure 4. The equilibrium swelling ratio of opaque gels. The swelling ratio is plotted as a function of the mole fraction of the cross-linker in the upper figure. The reaction temperature is fixed at 20 °C. In the lower figure, the swelling ratio is plotted as a function of the reaction temperature. In this series, the mole fraction of the cross-linker is fixed at 0.2. Here, d is the diameter of the cylindrical gel in the equilibrium state that is gelled in a capillary of an inner diameter of d₀.

Figure 4. The equilibrium swelling ratio of opaque gels. The swelling ratio is plotted as a function of the mole fraction of the cross-linker in the upper figure. The reaction temperature is fixed at 20 °C. In the lower figure, the swelling ratio is plotted as a function of the reaction temperature. In this series, the mole fraction of the cross-linker is fixed at 0.2. Here, d is the diameter of the cylindrical gel in the equilibrium state that is gelled in a capillary of an inner diameter of d₀.

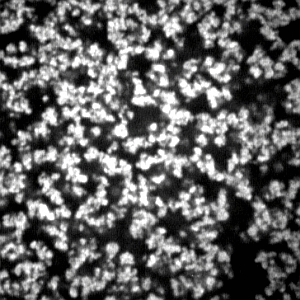
In Figure 5, we show the CLSM images of the opaque gels. In the first series, the sample gels are prepared by changing the mole fraction of the cross-linker from 0.2 to 0.5 under a constant total concentration of the pre-gel solution at 700 mM and at the reaction temperature of 20 °C. The gel is also prepared at a constant mole fraction of the cross-linker of 0.2 and changing the reaction temperature from 20 to 0 °C. Since the polymer network of the gel is labeled by the fluorescence dye, the bright portion of the image corresponds to the region where the concentration of the polymer network is higher. In contrast, the darker portion corresponds to the region where the density of the polymer network is lower. In the case of the gel that was prepared at the cross-linker concentration of 0.2 and at the reaction temperature of 20 °C, the brighter portion is distributed in the observed area rather uniformly. On the other hand, the spherical particles are aggregated to form the gel at a higher concentration region of the cross-linker and/or at lower reaction temperatures. The formation of the spherical particles becomes dominant when the mole fraction of the cross-linker becomes higher than 0.3 or the reaction temperature is lower than 10 °C. It is worth noting here that the fluorescence light intensity at the background portion of the image is not weak, even in the case of the CLSM imaging, if the thicker gel is used as the sample. This then prevents the detailed analysis of the images. We therefore used the thinner gels as the sample, which considerably improved the quality of the captured images as shown in Figure 5. All the images shown in Figure 5 are the as-obtained images without image enhancement.

It becomes clear from the CLSM observation of the gel structure that the polymer network of the opaque gel consists of aggregates of spherical particles. It may be natural to assume that the images of the opaque gel can be characterized by two parameters. One is the diameter of the spherical particles, and the other is the distribution of the particles in the image area. The diameter of particles is directly measured on the computer. More than 100 particles are randomly chosen from the image and measured using the image analyzing software. Several images are used to determine the average diameter of the colloid particle for one preparation condition. The resolution of the present CLSM is not enough to determine the exact diameter of the particles in the gel that was prepared at the cross-linker concentration of 0.2. Therefore, the average diameter of the particles is determined in the mole fraction of the cross-linker higher than 0.3 and is given in the Table 1. It is found that the diameter of the particles increases from 180 to 420 nm as the mole fraction of the cross-linker is increased from 0.3 to 0.5.

Figure 5. The confocal laser scanning microscope (CLSM) images of the opaque gels. The objective lens used here is 100× and the numerical aperture is 1.4. One side of the image corresponds to 28 µm. In the right column, the images of the gel gained by changing the mole fraction of the cross-linker are shown. In the bottom, the reaction temperature dependence of the image is shown. The total concentration of the gel is 700 mM.

Figure 5. The confocal laser scanning microscope (CLSM) images of the opaque gels. The objective lens used here is 100× and the numerical aperture is 1.4. One side of the image corresponds to 28 µm. In the right column, the images of the gel gained by changing the mole fraction of the cross-linker are shown. In the bottom, the reaction temperature dependence of the image is shown. The total concentration of the gel is 700 mM.

All of the structures shown in Figure 5 exhibit a very ramified structure. One of the possible analyses of such a structure is in terms of fractals [12]. The images given in Figure 5 are, of course, two-dimensional slices of the three-dimensional polymer network as it exists in the gel. Therefore, all of the analysis of the CLSM images is made in terms of a two-dimensional projection of the three-dimensional objects. The relationship between the radius of the sampling circle, r, and the total mass of the particle in the sampling circle, M, is expressed as follows:

(7)

Here, D is the fractal dimension. The total mass of the particle in the sampling circle is proportional to the number of particles in it. Then, the number of particles in the sampling circle is proportional to the area that is occupied by the particles, that is, the area of the brighter region. The area of the bright region in the sampling circle, σ, is measured as a function of the sampling concentric circles, which are drawn in the center of the image. A double logarithmic plot of r and σ is given in Figure 6.

Figure 6. The double logarithmic plot of r (in units of micrometers) and σ (in units of squared micrometers). Only typical results are shown here. The squares are the mole fraction of the cross-linker of 0.2, and the circles are the mole fraction of the cross-linker of 0.5, at a total concentration of 700 mM. The straight lines are the results of the least squares fit.

Figure 6. The double logarithmic plot of r (in units of micrometers) and σ (in units of squared micrometers). Only typical results are shown here. The squares are the mole fraction of the cross-linker of 0.2, and the circles are the mole fraction of the cross-linker of 0.5, at a total concentration of 700 mM. The straight lines are the results of the least squares fit.

The results obtained here exhibit the linear behavior expected of fractals. The solid lines in this figure are the least squares fit to the results. From the slopes of these straight lines, as well as those of many datasets, the fractal dimensions of the aggregates are determined. The average values of the fractal dimension thus obtained are also summarized in Table 1. The spatial distribution of the particles in the two-dimensional slices is a fractal of D ~ 1.6 when the mole fraction of the cross-linker is higher than 0.3. On the other hand, a fractal dimension of D = 2.0 is obtained for the gel in which the mole fraction of the cross-linker is 0.2. This is indicative of the uniform spatial distribution of the mass in the area of the image. In addition to these analyses, the fraction of the total brighter region to the area of the whole image is measured, and the values are also given in Table 1.

Table 1. Cross-linker concentration dependence of the structural parameters of the gels.

Mole fraction of cross-linker	0.2	0.3	0.4	0.5
Diameter of particle (×102 nm)	–	1.8	3.0	4.2
Fractal dimension	2.0	1.6	1.6	1.5
Fraction of total occupied area	–	0.44	0.33	0.23
Density of particle (×103 kg/m3)	–	1.27	1.15	1.22

The reaction temperature of the gel is 20.0 °C.

Table 1. Cross-linker concentration dependence of the structural parameters of the gels.

Mole fraction of cross-linker	0.2	0.3	0.4	0.5
Diameter of particle (×102 nm)	–	1.8	3.0	4.2
Fractal dimension	2.0	1.6	1.6	1.5
Fraction of total occupied area	–	0.44	0.33	0.23
Density of particle (×103 kg/m3)	–	1.27	1.15	1.22

The reaction temperature of the gel is 20.0 °C.

The images that are gained by changing the reaction temperature are analyzed in the same manner, and the results of the analysis are summarized in Table 2. In this series of experiments, the mole fraction of the cross-linker is fixed at 0.2. When the gel of this composition is prepared at a temperature of 20.0 °C, the radius of the spherical particle is smaller than the resolution limit of the present CLSM system, and hence, the spatial distribution of the particles is uniform. It is, however, found that the aggregated structure of the particles becomes clearer as the reaction temperature is lowered. The fractal dimension of the images, thus, can also be determined.

Table 2. Reaction temperature dependence of the structural parameters of the gels.

Reaction temperature (°C)	0	10.0
Diameter of particle (×102 nm)	2.4	1.6
Fractal dimension	1.7	1.7
Fraction of total occupied area	0.58	0.84
Density of particle (×103 kg/m3)	0.66	0. 69

The mole fraction of the cross-linker is 0.2.

Table 2. Reaction temperature dependence of the structural parameters of the gels.

Reaction temperature (°C)	0	10.0
Diameter of particle (×102 nm)	2.4	1.6
Fractal dimension	1.7	1.7
Fraction of total occupied area	0.58	0.84
Density of particle (×103 kg/m3)	0.66	0. 69

The mole fraction of the cross-linker is 0.2.

The CLSM image shows a thin slice of the observed sample. Thus, it is regarded as the two-dimensional projection of the observation volume to the focal plane. The observation volume of the image is known because both the thickness and the sides of the image are known. Since the opaque gels studied here do not swell and/or shrink in water, the total mass in the observation volume is conserved before and after the gel is formed. The total mass in the observation volume, thus, can be calculated from the initial concentration of the pre-gel solution. On the other hand, the total number of particles in the observation volume can be also calculated from the average diameter of the spherical particles and the area of the total brighter region in the image. This indicates that the average density of the spherical particles is determined from the structural parameters by assuming all the reagents are polymerized into the particles. The average densities of the particle thus determined are given in Table 1 and Table 2. The results indicate that the density of the spherical particles, which formed in the opaque poly(acrylamide) gel, is large. The results indicate that the dense spherical particles are spontaneously formed and aggregate to form the opaque gel in the higher concentration region of the cross-linking agent. If all the constituents are uniformly distributed in the observation volume, the density of the polymer network of the gel becomes about 0.06 × 10³ kg/m³. Indeed, the average density of the polymer network of the gel alone is almost the same with this value. In contrast, the densities of the particles that are given in the Table 1 are much higher and are rather close to the density of the constituents in the solid state. Both the main constituents and the cross-linker are, hence, densely cross-linked within the spherical particles. In the case of the results given in Table 2, the density of the spherical particles is smaller than that given in Table 1, though it is still ten times larger than the simple average density of the polymer network. The results, therefore, suggest strongly that the polymer network of the gels that are shown in the bottom column of Figure 5 contain a considerable amount of dangling chains. The dangling chains cannot be observed by the CLSM, because they are chains of molecular size and fluctuate, due to the Brownian movement. The presence of the dangling chains, therefore, should be checked by other experimental techniques. In both cases, however, the density of the spherical particles is large, and hence, the particles are regarded as hard colloid particles.

We find that the opaque gel consists of the aggregates of the spherical colloid particles of a sub-micrometer size. The density of the particles is much higher and is rather close to that of the constituents in the solid state. These results further suggest that the dense particles are spontaneously formed during the chemical reaction, and then, they coagulate by the diffusion limited aggregation process and/or the cluster-cluster aggregation process of the colloid particles, which leads to the formation of the fractal structure of the aggregate [13,14,15,16,17]. Hereafter, the gel that consists of the aggregate of the colloidal particles is called the colloid gel in the later discussions for the sake of simplicity. On the other hand, the uniform gel that consists of the molecular network of polymers is called the network gel.

3.2. Frictional Properties of Opaque Gel

Whenever the structure of the material is solved, many researchers intend to find the relationship between the structure and the properties of the material. In our case, it may be natural to ask how the structure of the gel, which is the aggregate of the colloid particles, is related to the properties, say, the mechanical properties of the gel. The mechanical properties of a gel are related to each other by the collective diffusion coefficient of the gel as follows:

(8)

Here, K, µ and f represent the osmotic bulk modulus, the shear modulus and the friction coefficient between the polymer network of the gel and the fluid. The friction coefficient of the gel is determined by using Equation (1) experimentally. On the other hand, the scaling indicates that the friction coefficient can be written in terms of the molecular parameters, such as the viscosity of the fluid passing through the polymer network, η, and the frictional pore size, ξ², as follows.

(9)

In the case of the network gel, it is natural to assume that the parameter, ξ, represents the correlation length of the gel that, in a good solvent, corresponds to the average distance between the neighboring contact points of the polymers [18].

In the present case, the elasticity of the gel is easy to measure, but is difficult to analyze, because the aggregated structure of the colloid particles is complex. In contrast, the frictional properties of the gel may be much easier to analyze, since the friction is determined simply by the structure of the colloid gel. However, the characteristics of the heterogeneous structure of the opaque gel, which have been clarified in the previous section, should be accurately taken into account to analyze the frictional property of the opaque gel.

The time elution time course for the gel is measured using the gels that are prepared at various concentrations of the cross-linker. The results are calculated according to Equation (5), and then, the logarithm of the relative change of the height of the water inside the capillary, [h₀ – h(t)]/h₀, is plotted as a function of time in Figure 7. The results are well expressed by straight lines. The slopes of the straight lines are obtained by a least squares method, and then, the friction coefficients of the opaque gels are calculated from the characteristic time by using Equation (6). The friction coefficients of the gels thus obtained are plotted as a function of the concentration of the cross-linker in Figure 8 with the previous results in the form of double logarithmic plot.

Figure 7. Semi-logarithmic plot of the relative height change. The mole fraction of the cross-linker is 0.5, 0.45, 0.4, 0.35 and 0.3, from top to bottom.

Figure 7. Semi-logarithmic plot of the relative height change. The mole fraction of the cross-linker is 0.5, 0.45, 0.4, 0.35 and 0.3, from top to bottom.

Figure 8. The double logarithmic plot of the cross-linker concentration dependence of the friction coefficient. The present results are plotted with the previous results shown in [4] (left); The close up view of the present results (right). The closed symbols in the right figure are the calculated values using Equation (11).

Figure 8. The double logarithmic plot of the cross-linker concentration dependence of the friction coefficient. The present results are plotted with the previous results shown in [4] (left); The close up view of the present results (right). The closed symbols in the right figure are the calculated values using Equation (11).

It is clear from this figure that the friction is enormous in the concentration region of the cross-linker, less than about 10 mol %, in which most gels are transparent. This strongly suggests that the polymer network is a mesh of molecular size in this concentration region of the cross-linker; the network gel. However, it is also found that the friction coefficient of the opaque gel decreases more than three orders of magnitude from that of the transparent gels if the mole fraction of the cross-linker is higher than 10 mol %. This drastic decrease of the friction coefficient of the gel corresponds well to the formation of the colloid gel structure, as shown by the CLMS study in the present section; the colloid gel. It may be difficult to discuss the frictional properties of the network gel in terms of the molecular structure of the polymer network, because of the lack of detailed information on the structure of the polymer network. In contrast, we already have structural information on the colloid gel, which corresponds to the gels prepared at the higher concentration region of the cross-linker. We therefore made the CLSM observation of the gels that were used in the friction measurements. The CLSM images thus obtained are shown in Figure 9.

Figure 9. The CLSM images of the gels that were used in the friction measurements. The mole fraction of the cross-linker is 0.3, 0.4 and 0.5, from left to right. The image size is 30 µm × 30 µm.

Figure 9. The CLSM images of the gels that were used in the friction measurements. The mole fraction of the cross-linker is 0.3, 0.4 and 0.5, from left to right. The image size is 30 µm × 30 µm.

The quality of the images is deteriorated more than the images given in Figure 5, because the sample gel observed here is the bulk gel of a thickness of about 0.5 mm, that is the radius of the capillary. It is, however, clear from these images that the darker regions are spreading to the whole region of the images. Since the density of the particles is almost the same with the constituents in the solid state, the flowing water thus cannot penetrate into the colloid particles. The polymer network of the opaque gel is, therefore, regarded as the assembly of hard spherical particles rather than the molecular network. The friction is, therefore, small in such an inhomogeneous gel, since water flows choosing mainly the darker region of the image, which serve as a more open and free path, while avoiding the colloidal particles, which block the flow. The water of the viscosity, η, that flows in the gel experiences the hydrodynamic friction of the hard spheres of the radius, R, that is suspended in a fluid. We therefore expect that the hydrodynamic friction of the opaque gel for the water passing through the gel can be written as follows:

f = N6πηR

(10)

Here, N represents the number of the colloid particles that is contained in a unit volume of gel. Both the number and the radius of the colloid particle that consists of the polymer network of the opaque gel can be derived from the CLSM images that are shown in Figure 9. Since the particles are localized in the brighter region of the CLSM image, the area of the brighter region is proportional to the number of particles in the gel. We therefore obtain two structural parameters of the colloid gel from the CLSM image, namely the diameter of the colloid particle and the area occupied by the colloid particle, d = 2R and σ, respectively. The results of the image analysis are given in Figure 10.

The number of particles in a unit volume of gel is expressed as σ/πR²V. Here, the observation volume of the CLSM image is given as V = σ₀T, where T and σ₀ are the thickness of the focal plane and the actual area of the image, respectively. Substitution of these parameters into Equation (9) yields the following relationship.

(11)

Figure 10. The structural parameters of the opaque gel. The diameter of the colloid particle is plotted as a function of the mole fraction of the cross-linker (left); The right figure represents the cross-linker concentration dependence of the relative occupied area by the colloid particle. Both parameters are plotted in the double logarithmic manner. Lines are drawn only to guide the eye.

Figure 10. The structural parameters of the opaque gel. The diameter of the colloid particle is plotted as a function of the mole fraction of the cross-linker (left); The right figure represents the cross-linker concentration dependence of the relative occupied area by the colloid particle. Both parameters are plotted in the double logarithmic manner. Lines are drawn only to guide the eye.

Since all these values are known, the friction coefficient of the gel can be calculated. The results are also given in the right subfigure of Figure 8. The relationship between the calculated values of the friction coefficient and the mole fraction of the cross-linker shows the same tendency with the experimental results, but the values thus calculated are still about one-half of the measured values [19].

The discrepancy between the calculated values and the experimental values can be explainable as follows. The thickness of the focal plane of the CLSM image is thin, but finite. The particle size of the colloid gel is almost one-half of the thickness of the focal plane, as shown in the Figure 10. The overlap of the smaller particles behind the larger particles is unavoidable and is also undetectable by the CLSM observation at the present resolution. It is, hence, natural to assume that the maximum number of particles in the image area is estimated to be about twice that of the calculated one. Taking into account these facts, the agreement of the calculated values with the experimental values is satisfactory. Here, we use the simplest model to analyze the frictional property of the colloid gel. Namely, all the hydrodynamic interaction between the particles is neglected, and also, the particles are regarded as independent, single particles. Although the model is still crude, it contains the essential features of the frictional property of the colloid gel.

3.3. Friction and Structure of Opaque Gel

As we have seen above, the mechanical property of the gel and the structure of the gel are closely related each other. When the concentration of the cross-linker is increased at a constant total concentration of the gel, the network structure of the gel changes from the molecular network at the lower concentration region of the cross-linker to the colloid gel at the higher concentration region of the cross-linker. This change of the network structure occurs rather drastically at a mole fraction of the cross-linker of about 0.2 to 0.3. The friction of the gel decreases more than three orders of magnitude around this concentration region of the cross-linker. This drastic change may be attributed to the structural transition of the polymer network from the molecular network gel to the colloid gel.

The impression of the CLSM images gained in the structural study and that of the frictional study are somewhat different. The diameter of the colloid particles formed in the gel is rather larger in the friction case compared to the structural case, even for the same composition of the gel. The occupied area by the colloid particle in the image is also larger in the friction case. These differences may be caused by the differences in the reaction temperature. In the case of the structural study, the reaction temperature is strictly controlled to clarify the effects of the reaction temperature on the structure of the gel. On the other hand, the gel should be prepared in the glass capillary in the case of the frictional study. The temperature rise due to the UV irradiation is, hence, unavoidable. Although the relationship between the frictional property and the structure in opaque gel is clarified, a detailed study is still required for the full understanding of the structure-property relationship of the gel.

Some aspects of the polymer network dynamics that are related to the water flow through the gel are worth noting here [20,21]. It has been shown in the early studies of the friction of gel that the velocity of water flow in the gel is fast at the beginning and then decreases with time to a steady-state value. In the case of the transparent gels, this requires more than three hours to achieve a steady state, even in a 1 mm-thick gel. The polymer network of the gel easily deforms from the equilibrium state, due to the drag force of the flowing water. The restoring force due to the rubber elasticity arises, and it competes with the drag force. The balance between these forces determines the characteristic time interval that is required to attain the steady-state flow of water, as given by the collective diffusion coefficient of the gel, which is given by Equation 8. This characteristic time is known to be proportional to the inverse of the square of the typical size of the gel. In addition to this, the flow time course is expressed by the superposition of the exponential functions in the case of the transparent gels. These are the reasons for such a long equilibrium time for the stationary state. In contrast, the flow time course of the opaque gel is expressed by a single exponential function, as shown in Figure 8. Besides, the velocity of the flowing water is constant throughout the measurement, even in the thicker gels of about 5 mm or more. The polymer network dynamics of the opaque gel is totally different from that of the transparent gel. The differences in the network dynamics may also be attributed to the structure of opaque gels and strongly suggest that the opaque gels do not contain long, flexible chains that can deform under the flow of water and exhibit rubber elasticity. These results are also confirmed by the fact that the opaque gels do not swell in water, and their swelling ratios are almost unity, as shown in Figure 4.

4. Conclusions

We review recent studies on the structure and the property of opaque poly(acrylamide) gels. The structural study is performed in real space by using CLSM. The results indicate that the opaque gels of acrylamide consist of the fractal aggregates of the colloid particles. The density of the particles is much higher than the gels in the uniform state.

The frictional property of the gels is determined independently. The friction of the gels decreases more than three orders of magnitudes when the mole fraction of the cross-linker exceeds 0.3. The real-space structure of the gels is also determined after the measurements of friction. The friction of the gels is calculated from the structural parameters of the gels, which is determined by the structural study. Both the experimental values of the friction and the friction that is calculated from the structural parameters of the gels are within good agreement if the limits of the resolution of the CLSM measurements are taken into account. The dynamics of the solvent flow in the gels is also well explained by the structural characteristics of the opaque gels.