Polypeptide-Nanoparticle Interactions and Corona Formation Investigated by Monte Carlo Simulations
Abstract
:1. Introduction
2. Model
3. Results and discussion
3.1. Role of pH and NP Surface Charge Density in the Formation of Complexes
3.1.1. Titration Curves
3.1.2. PP Chain Conformations
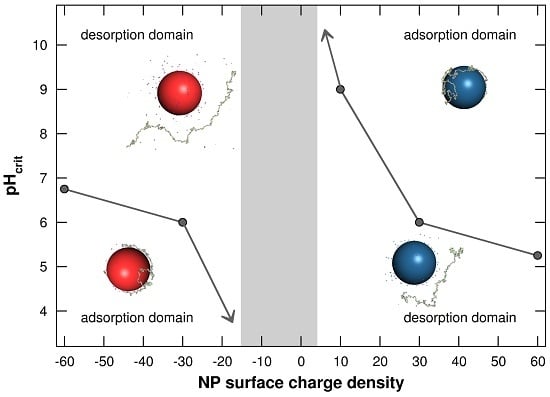
3.1.3. Adsorption/Desorption Limits
3.2. Role of Salt Valency in the Formation of Complexes
3.2.1. Titration Curves
3.2.2. PP Chain Conformations
3.2.3. Stability of Complexes
3.2.4. Distribution of AAs at the NP Surface
3.2.5. Adsorption/Desorption Limits
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Carter, D.C.; He, X.; Munson, S.H.; Twigg, P.D.; Gernert, K.M.; Broom, M.B.; Miller, T.Y. Three-dimensional structure of human serum albumin. Science 1989, 244, 1195–1198. [Google Scholar] [CrossRef] [PubMed]
- Curry, S.; Mandelkow, H.; Brick, P.; Franks, N. Crystal structure of human serum albumin complexed with fatty acid reveals an asymmetric distribution of binding sites. Nat. Struct. Biol. 1998, 5, 827–835. [Google Scholar] [CrossRef] [PubMed]
- De Wolf, F.A.; de Brett, G.M. Ligand-binding proteins: Their potential for application in systems for controlled delivery and uptake of ligands. Pharmacol. Rev. 2000, 52, 207–236. [Google Scholar] [PubMed]
- Yang, F.; Zhang, Y.; Liang, H. Interactive association of drugs binding to human serum albumin. Int. J. Mol. Sci. 2014, 15, 3580–3595. [Google Scholar] [CrossRef] [PubMed]
- Bos, O.J.; Labro, J.F.; Fischer, M.J.; Wilting, J.; Janssen, L.H. The molecular mechanism of the neutral-to-base transition of human serum albumin. Acid/base titration and proton nuclear magnetic resonance studies on a large peptic and a large tryptic fragment of albumin. J. Biol. Chem. 1989, 264, 953–959. [Google Scholar] [PubMed]
- Peters, T., Jr. All about Albumin: Biochemistry, Genetics, and Medical Applications; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Ahmad, B.; Kamal, M.Z.; Khan, R.H. Alkali-induced conformational transition in different domains of bovine serum albumin. Protein Pept. Lett. 2004, 11, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, L.R.S.; Ortore, M.G.; Spinozzi, F.; Mariani, P.; Bernstorff, S.; Itri, R. The importance of protein-protein interactions on the pH-induced conformational changes of bovine serum albumin: A Small-angle x-ray scattering study. Biophys. J. 2010, 98, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Foster, J.F.; Samsa, E.G. Streaming orientation studies on denatured proteins. I. Heat denaturation of ovalbumin in acid media1. J. Am. Chem. Soc. 1951, 73, 3187–3190. [Google Scholar] [CrossRef]
- Foster, J.F.; Samsa, E.G. Streaming orientation studies on denatured proteins. III. Denaturation of ovalbumin in the presence of urea. J. Am. Chem. Soc. 1951, 73, 5388–5391. [Google Scholar] [CrossRef]
- El Kadi, N.; Taulier, N.; Le Huérou, J.Y.; Gindre, M.; Urbach, W.; Nwigwe, I.; Kahn, P.C.; Waks, M. Unfolding and refolding of bovine serum albumin at acid pH: Ultrasound and structural studies. Biophys. J. 2006, 91, 3397–3404. [Google Scholar] [CrossRef] [PubMed]
- Reyes, L.; Bert, J.; Fornazero, J.; Cohen, R.; Heinrich, L. Influence of conformational changes on diffusion properties of bovine serum albumin: A holographic interferometry study. Colloids Surf. B Biointerfaces 2002, 25, 99–108. [Google Scholar] [CrossRef]
- Yamasaki, M.; Yano, H.; Aoki, K. Differential scanning calorimetric studies on bovine serum albumin: II. Effects of neutral salts and urea. Int. J. Biol. Macromol. 1991, 13, 322–328. [Google Scholar] [CrossRef]
- Kumar, Y.; Tayyab, S.; Muzammil, S. Molten-globule like partially folded states of human serum albumin induced by fluoro and alkyl alcohols at low pH. Arch. Biochem. Biophys. 2004, 426, 3–10. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Huang, M.; Ye, W.; Chen, D.; He, S.; Ding, L.; Yao, Y.; Wan, L.; Xu, J.; Miao, S. Conformational change of bovine serum albumin molecules at neutral pH in ultra-diluted aqueous solutions. J. Phys. Chem. B 2014, 118, 12207–12214. [Google Scholar] [CrossRef] [PubMed]
- Dobson, C.M. Protein folding and misfolding. Nature 2003, 426, 884–890. [Google Scholar] [CrossRef] [PubMed]
- Aramesh, M.; Shimoni, O.; Ostrikov, K.; Prawer, S.; Cervenka, J. Surface charge effects in protein adsorption on nanodiamonds. Nanoscale 2015, 7, 5726–5736. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Xu, Y.; Rana, S.; Miranda, O.R.; Dubin, P.L.; Rotello, V.M.; Sun, L.; Guo, X. Electrostatic selectivity in protein–nanoparticle interactions. Biomacromolecules 2011, 12, 2552–2561. [Google Scholar] [CrossRef] [PubMed]
- Jachimska, B.; Pajor, A. Physico-chemical characterization of bovine serum albumin in solution and as deposited on surfaces. Bioelectrochemistry 2012, 87, 138–146. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.A.; Urzúa, M.D.; Petri, D.F.S.; Dubin, P.L. Protein adsorption onto polyelectrolyte layers: Effects of protein hydrophobicity and charge anisotropy. Langmuir 2010, 26, 14032–14038. [Google Scholar] [CrossRef] [PubMed]
- Patil, S.; Sandberg, A.; Heckert, E.; Self, W.; Seal, S. Protein adsorption and cellular uptake of cerium oxide nanoparticles as a function of zeta potential. Biomaterials 2007, 28, 4600–4607. [Google Scholar] [CrossRef] [PubMed]
- Calzolai, L.; Laera, S.; Ceccone, G.; Gilliland, D.; Hussain, R.; Siligardi, G.; Rossi, F. Gold nanoparticles’ blocking effect on UV-induced damage to human serum albumin. J. Nanopart. Res. 2013, 15, 1–5. [Google Scholar] [CrossRef]
- Laera, S.; Ceccone, G.; Rossi, F.; Gilliland, D.; Hussain, R.; Siligardi, G.; Calzolai, L. Measuring protein structure and stability of protein–nanoparticle systems with synchrotron radiation circular dichroism. Nano Lett. 2011, 11, 4480–4484. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Chen, K.; Gu, H. Investigations on the interactions of proteins with polyampholyte-coated magnetite nanoparticles. J. Phys. Chem. B 2013, 117, 14129–14135. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Geng, X.-P.; Wang, B.-H.; Zhou, Y. Studies on the conformational change of adsorbed BSA onto a moderately hydrophobic surface at different denaturant concentrations and surface coverages. J. Colloid Interface Sci. 2010, 344, 468–474. [Google Scholar] [CrossRef] [PubMed]
- Vergaro, V.; Carlucci, C.; Cascione, M.; Lorusso, C.; Conciauro, F.; Scremin, B.F.; Congedo, P.M.; Cannazza, G.; Citti, C.; Ciccarella, G. Interaction between human serum albumin and different anatase TiO2 nanoparticles: A nano-bio interface study. Nanomater. Nanotechnol. 2015, 1. [Google Scholar] [CrossRef]
- Guan, Y.; Zhang, H.; Wang, Y. New insight into the binding interaction of hydroxylated carbon nanotubes with bovine serum albumin. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 124, 556–563. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, M.; Jain, N.; Mukhopadhyay, S. Insights into the mechanism of aggregation and fibril formation from bovine serum albumin. J. Phys. Chem. B 2011, 115, 4195–4205. [Google Scholar] [CrossRef] [PubMed]
- Juárez, J.; López, S.G.; Cambón, A.; Taboada, P.; Mosquera, V. Influence of electrostatic interactions on the fibrillation process of human serum albumin. J. Phys. Chem. B 2009, 113, 10521–10529. [Google Scholar] [CrossRef] [PubMed]
- Ozboyaci, M.; Kokh, D.B.; Corni, S.; Wade, R.C. Modeling and simulation of protein–surface interactions: achievements and challenges. Q. Rev. Biophys. 2016, 49. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.-W.; Wu, T.; Wang, Q.; Kang, Y. Induced stepwise conformational change of human serum albumin on carbon nanotube surfaces. Biomaterials 2008, 29, 3847–3855. [Google Scholar] [CrossRef] [PubMed]
- Voicescu, M.; Ionescu, S.; Angelescu, D.G. Spectroscopic and coarse-grained simulation studies of the BSA and HSA protein adsorption on silver nanoparticles. J. Nanopart. Res. 2012, 14, 1–13. [Google Scholar] [CrossRef]
- Raffaini, G.; Ganazzoli, F. Simulation study of the interaction of some albumin subdomains with a flat graphite surface. Langmuir 2003, 19, 3403–3412. [Google Scholar] [CrossRef]
- Rabe, M.; Verdes, D.; Seeger, S. Understanding cooperative protein adsorption events at the microscopic scale: A comparison between experimental data and monte carlo simulations. J. Phys. Chem. B 2010, 114, 5862–5869. [Google Scholar] [CrossRef] [PubMed]
- Barroso da Silva, F.L.; Boström, M.; Persson, C. Effect of charge regulation and ion–dipole interactions on the selectivity of protein–nanoparticle binding. Langmuir 2014, 30, 4078–4083. [Google Scholar] [CrossRef] [PubMed]
- Pellicane, G.; Cavero, M. Theoretical study of interactions of BSA protein in a NaCl aqueous solution. J. Chem. Phys. 2013, 138, 115103. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, S.; Seijo, M.; Stoll, S. A Monte Carlo study of weak polyampholytes: Stiffness and primary structure influences on titration curves and chain conformations. J. Phys. Chem. B 2007, 111, 8459–8467. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, S.; Seijo, M.; Carnal, F.; Stoll, S. Formation of complexes between nanoparticles and weak polyampholyte chains. Monte carlo simulations. Macromolecules 2011, 44, 1661–1670. [Google Scholar] [CrossRef]
- Carnal, F.; Clavier, A.; Stoll, S. Modelling the interaction processes between nanoparticles and biomacromolecules of variable hydrophobicity: Monte Carlo simulations. Environ. Sci. Nano 2015, 2, 327–339. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation-of-state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Majorek, K.A.; Porebski, P.J.; Dayal, A.; Zimmerman, M.D.; Jablonska, K.; Stewart, A.J.; Chruszcz, M.; Minor, W. Structural and immunologic characterization of bovine, horse, and rabbit serum albumins. Mol. Immunol. 2012, 52, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 5th ed.; W. H. Freeman and Company: New York, NY, USA, 2008. [Google Scholar]
- Kyte, J.; Doolittle, R.F. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982, 157, 105–132. [Google Scholar] [CrossRef]
- Gordon, H.L.; Valleau, J.P. A “partially clothed” pivot algorithm for model polyelectrolyte solutions. Mol. Simul. 1995, 14, 361–379. [Google Scholar] [CrossRef]
- Verdier, P.H.; Stockmayer, W.H. Monte Carlo calculations on the dynamics of polymers in dilute solutions. J. Chem. Phys. 1962, 36, 227–235. [Google Scholar] [CrossRef]
- Wall, F.T.; Mandel, F. Macromolecular dimensions obtained by an efficient Monte-Carlo method without sample attrition. J. Chem. Phys. 1975, 63, 4592–4595. [Google Scholar] [CrossRef]
- Reed, C.E.; Reed, W.F. Monte-Carlo study of titration of linear polyelectrolytes. J. Chem. Phys. 1992, 96, 1609–1620. [Google Scholar] [CrossRef]
- Ullner, M.; Jönsson, B.; Widmark, P.O. Conformational properties and apparent dissociation constants of titrating polyelectrolytes: Monte Carlo simulation and scaling arguments. J. Chem. Phys. 1994, 100, 3365–3366. [Google Scholar] [CrossRef]
- Foster, J.F. Some aspects of the structure and conformational properties of serum albumin. In Albumin Structure, Function and Uses; Rosenoer, V.M., Oratz, M., Rothschild, M.A., Eds.; Pergamon: Oxford, UK, 1977. [Google Scholar]
- Michnik, A.; Michalik, K.; Drzazga, Z. Stability of bovine serum albumin at different pH. J. Therm. Anal. Calorim. 2005, 80, 399–406. [Google Scholar] [CrossRef]
- Yamasaki, M.; Yano, H.; Aoki, K. Differential scanning calorimetric studies on bovine serum albumin: I. Effects of pH and ionic strength. Int. J. Biol. Macromol. 1990, 12, 263–268. [Google Scholar] [CrossRef]
- Itri, R.; Caetano, W.; Barbosa, L.R.S.; Baptista, M.S. Effect of urea on bovine serum albumin in aqueous and reverse micelle environments investigated by small angle X-ray scattering, fluorescence and circular dichroism. Braz. J. Phys. 2004, 34, 58–63. [Google Scholar] [CrossRef]
- Tanford, C.; Buzzell, J.G. The viscosity of aqueous solutions of bovine serum albumin between pH 4.3 and 10.5. J. Phys. Chem. 1956, 60, 225–231. [Google Scholar] [CrossRef]
- Mouat, M.F.; Manchester, K.L. The intracellular ionic strength of red cells and the influence of complex formation. Comp. Haematol. Int. 1998, 8, 58–60. [Google Scholar] [CrossRef]
- Arya, G.; Schlick, T. A tale of tails: How histone tails mediate chromatin compaction in different salt and linker histone environments. J. Phys. Chem. A 2009, 113, 4045–4059. [Google Scholar] [CrossRef] [PubMed]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Dover Publications: New York, NY, USA, 1999. [Google Scholar]










© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carnal, F.; Clavier, A.; Stoll, S. Polypeptide-Nanoparticle Interactions and Corona Formation Investigated by Monte Carlo Simulations. Polymers 2016, 8, 203. https://doi.org/10.3390/polym8060203
Carnal F, Clavier A, Stoll S. Polypeptide-Nanoparticle Interactions and Corona Formation Investigated by Monte Carlo Simulations. Polymers. 2016; 8(6):203. https://doi.org/10.3390/polym8060203
Chicago/Turabian StyleCarnal, Fabrice, Arnaud Clavier, and Serge Stoll. 2016. "Polypeptide-Nanoparticle Interactions and Corona Formation Investigated by Monte Carlo Simulations" Polymers 8, no. 6: 203. https://doi.org/10.3390/polym8060203
APA StyleCarnal, F., Clavier, A., & Stoll, S. (2016). Polypeptide-Nanoparticle Interactions and Corona Formation Investigated by Monte Carlo Simulations. Polymers, 8(6), 203. https://doi.org/10.3390/polym8060203