Modeling the Temperature Dependence of Dynamic Mechanical Properties and Visco-Elastic Behavior of Thermoplastic Polyurethane Using Artificial Neural Network
Abstract
:1. Introduction
1.1. Dynamic Mechanical Analysis
1.2. Relaxation Transitions in Polymers
1.3. Stiffness-Temperature Model of Thermoplastic Urethanes
1.4. Artificial Neural Networks
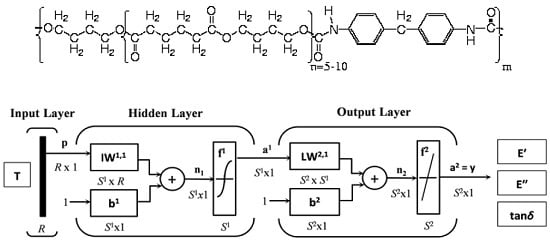
2. Materials and Methods
Artificial Neural Network Modeling
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Drobny, J.G. Handbook of Thermoplastic Elastomers, 2nd ed.; Elsevier: Oxford, UK, 2014. [Google Scholar]
- Krmela, J.; Krmelová, V. Dynamic Experiment of Parts of Car Tyres. Procedia Eng. 2017, 187, 763–768. [Google Scholar] [CrossRef]
- Patton, S.T.; Chen, C.; Hu, J.; Grazulis, L.; Schrand, A.M.; Roy, A.K. Characterization of Thermoplastic Polyurethane (TPU) and Ag-Carbon Black TPU Nanocomposite for Potential Application in Additive Manufacturing. Polymers 2017, 9, 6. [Google Scholar] [CrossRef]
- Prisacariu, C. Polyurethane Elastomers: From Morphology to Mechanical Aspects; Springer: Wien, Austria, 2011. [Google Scholar]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ramachandran, V.S.; Paroli, R.M.; Beaudoin, J.J.; Delgado, A.H. Handbook of Thermal Analysis of Construction Materials; Noyes Publications/William Andrew Pub: Norwich, NY, USA, 2002. [Google Scholar]
- Menczel, J.D.; Prime, R.B. Thermal Analysis of Polymers: Fundamentals and Applications; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Huh, D.S.; Cooper, S.L. Dynamic mechanical properties of polyurethane block polymers. Polym. Eng. Sci. 1971, 11, 369–376. [Google Scholar] [CrossRef]
- Gabbott, P. Principles and Applications of Thermal Analysis; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ward, I.M.; Sweeney, J. An Introduction to the Mechanical Properties of Solid Polymers, 2nd ed.; Wiley: Chichester, UK, 2004. [Google Scholar]
- Mahieux, C.A.; Reifsnider, K.L. Property modeling across transition temperatures in polymers: A robust stiffness-temperature model. Polymer 2001, 42, 3281–3291. [Google Scholar] [CrossRef]
- Richeton, J.; Schlatter, G.; Vecchio, K.S.; Rémond, Y.; Ahzi, S. Unified model for stiffness modulus of amorphous polymers across transition temperatures and strain rates. Polymer 2005, 46, 8194–8201. [Google Scholar] [CrossRef]
- Kopal, I.; Bakošová, D.; Koštial, P.; Jančíková, Z.; Valíček, J.; Harničárová, M. Weibull distribution application on temperature dependence of polyurethane storage modulus. Int. J. Mater. Res. 2016, 107, 472–476. [Google Scholar] [CrossRef]
- Rinne, H. The Weibull Distribution: A Handbook; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity, 2nd ed.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Li, Y.; Tang, S.; Abberton, B.C.; Kröger, M.; Burkhart, C.; Jiang, B.; Papakonstantopoulos, G.J.; Poldneff, M.; Liu, W.K. A predictive multiscale computational framework for viscoelastic properties of linear polymers. Polymer 2012, 53, 5935–5952. [Google Scholar] [CrossRef]
- Li, Y.; Abberton, B.C.; Kröger, M.; Liu, W.K. Challenges in multiscale modeling of polymer dynamics. Polymers 2013, 5, 751–832. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks, 1st ed.; Prentice Hall: New York, NY, USA, 1994. [Google Scholar]
- Zhang, Z.; Friedrich, K. Artificial neural networks applied to polymer composites: A review. Compos. Sci. Technol. 2003, 63, 2029–2044. [Google Scholar] [CrossRef]
- Sifaoui, A.; Abdelkrim, A.; Benrejeb, M. On the Use of Neural Network as a Universal Approximator. Int. J. Sci. Tech. Control Comput. Eng. 2008, 2, 386–399. [Google Scholar]
- Bessa, M.A.; Bostanabad, R.; Liu, Z.; Hu, A.; Apley, D.W.; Brinson, C.; Chen, W.; Liu, W.K. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 2017, 320, 633–667. [Google Scholar] [CrossRef]
- Le, B.A.; Yvonnet, J.; He, Q.C. Computational homogenization of nonlinear elastic materials using neural networks. Int. J. Numer. Meth. Eng. 2015, 104, 1061–1084. [Google Scholar] [CrossRef]
- Norgaard, M.; Ravn, O.; Poulsen, N.K.; Hansen, L.K. Neural Networks for Modeling and Control of Dynamic Systems; Springer: Berlin, Germany, 2002. [Google Scholar]
- Jin, D.; Lin, A. Advances in Computer Science, Intelligent System and Environment; Springer: Berlin, Germany, 2011. [Google Scholar]
- Aliev, R.; Bonfig, K.; Aliew, F. Soft Computing; Verlag Technic: Berlin, Germany, 2000. [Google Scholar]
- Bhowmick, A.K.; Stephens, H.L. Handbook of Elastomers, 2nd ed.; CRC-Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Qi, Z.N.; Wan, Z.H.; Chen, Y.P. A comparative DSC method for physical aging measurement of polymers. Polym. Test. 1993, 12, 185–192. [Google Scholar] [CrossRef]
- Freeman, J.A.; Skapura, D.M. Neural Networks Algorithms, Applications, and Programming Techniques; Addison-Wesley Publishing Company: Boston, MA, USA, 1991. [Google Scholar]
- Auer, P.; Burgsteiner, H.; Maass, W.A. A learning rule for very simple universal approximators consisting of a single layer of perceptrons. Neural Netw. 2008, 21, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Shanmuganathan, S.; Samarasinghe, S. Artificial Neural Network Modelling; Springer: Berlin, Germany, 2016. [Google Scholar]
- Du, K.L.; Swamy, M.N.S. Neural Networks and Statistical Learning; Springer: Berlin, Germany, 2014. [Google Scholar]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox™ User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Optimal division of data for neural network models in water resources applications. Water Resour. Res. 2002, 38, 2-1–2-11. [Google Scholar] [CrossRef]
- Trebar, M.; Susteric, Z.; Lotric, U. Predicting mechanical properties of elastomers with neural networks. Polymer 2007, 48, 5340–5347. [Google Scholar] [CrossRef]
- Zhang, Z.; Klein, P.; Friedrich, K. Dynamic mechanical properties of PTFE based short carbon fibre reinforced composites: Experiment and artificial neural network prediction. Compos. Sci. Technol. 2002, 62, 1001–1009. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Hagan, M.T.; Menhaj, M. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1999, 5, 989–999. [Google Scholar] [CrossRef] [PubMed]
- Croeze, A.; Pittman, L.; Reynolds, W. Nonlinear Least-Squares Problems with the Gauss-Newton and Levenberg-Marquardt Methods; University of Mississippi: Oxford, UK, 2012. [Google Scholar]
- Fairbank, M.; Alonso, E. Efficient Calculation of the Gauss-Newton Approximation of the Hessian Matrix in Neural Networks. Neural Comput. 2012, 24, 607–610. [Google Scholar] [CrossRef] [PubMed]
- Wackerly, D.; Mendenhall, W.; Scheaffer, R.L. Mathematical Statistics with Applications, 7th ed.; Thomson Higher Education: Belmont, TN, USA, 2008. [Google Scholar]
- Barnes, R.J. Matrix Differentiation; University of Minnesota: Minneapolis, MN, USA, 2017. [Google Scholar]
- Madić, M.J.; Radovanović, M.R. Optimal Selection of ANN Training and Architectural Parameters Using Taguchi Method: A Case Study. FME Trans. 2011, 39, 79–86. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Zhang, T.; Yu, B. Boosting with Early Stopping: Convergence and Consistency. Ann. Stat. 2005, 33, 1538–1579. [Google Scholar] [CrossRef]
- Syed, A.H.; Munir, A. Distribution of Mean of Correlation Coefficients: Mean of Correlation Coefficients; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2012. [Google Scholar]
- Nematollahi, M.; Jalali-Arani, A.; Golzar, K. Organoclay maleated natural rubber nanocomposite. Prediction of abrasion and mechanical properties by artificial neural network and adaptive neuro-fuzzy inference. Appl. Clay Sci. 2014, 97–98, 187–199. [Google Scholar] [CrossRef]
- Simon, L. An Introduction to Multivariable Mathematics; Morgan & Claypool: St. Louis, CA, USA, 2008. [Google Scholar]
- Shi, F.; Wang, X.C.; Yu, L.; Li, Y. MATLAB 30 Case Analysis of MATLAB Neural Network; Beijing University Press: Beijing, China, 2009. [Google Scholar]
- Wong, S.S.M. Computational Methods in Physics and Engineering, 2nd ed.; World Scientic Publishing: New York, NY, USA, 1977. [Google Scholar]
- Suzuki, K. Artificial Neural Networks—Industrial and Control Engineering Applications; InTech: Rijeka, Croatia, 2011. [Google Scholar]








© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopal, I.; Harničárová, M.; Valíček, J.; Kušnerová, M. Modeling the Temperature Dependence of Dynamic Mechanical Properties and Visco-Elastic Behavior of Thermoplastic Polyurethane Using Artificial Neural Network. Polymers 2017, 9, 519. https://doi.org/10.3390/polym9100519
Kopal I, Harničárová M, Valíček J, Kušnerová M. Modeling the Temperature Dependence of Dynamic Mechanical Properties and Visco-Elastic Behavior of Thermoplastic Polyurethane Using Artificial Neural Network. Polymers. 2017; 9(10):519. https://doi.org/10.3390/polym9100519
Chicago/Turabian StyleKopal, Ivan, Marta Harničárová, Jan Valíček, and Milena Kušnerová. 2017. "Modeling the Temperature Dependence of Dynamic Mechanical Properties and Visco-Elastic Behavior of Thermoplastic Polyurethane Using Artificial Neural Network" Polymers 9, no. 10: 519. https://doi.org/10.3390/polym9100519
APA StyleKopal, I., Harničárová, M., Valíček, J., & Kušnerová, M. (2017). Modeling the Temperature Dependence of Dynamic Mechanical Properties and Visco-Elastic Behavior of Thermoplastic Polyurethane Using Artificial Neural Network. Polymers, 9(10), 519. https://doi.org/10.3390/polym9100519