An Insight into the Flammability of Some Bio-Based Polyesters
Abstract
:1. Introduction
2. Methodology
2.1. Materials
2.2. Experiments
2.3. Method
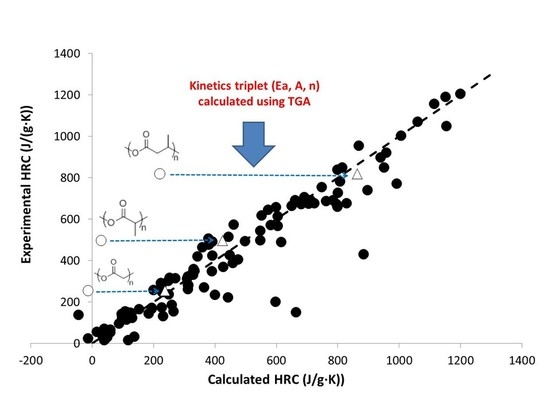
3. Results and Discussion
3.1. Activation Energy of Pyrolysis
3.2. Calculation of Activation Energies from Chemical Structure
4. Reaction Model
5. Discussion about the Flammability of PHB
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Walters, N.; Lyon, R.E. Molar Group Contributions to Polymer Flammability. J. Appl. Polym. Sci. 2003, 87, 548–563. [Google Scholar] [CrossRef]
- Lyon, R.E.; Takemori, M.T.; Safronova, N.; Stoliarov, S.I.; Walters, R.N. A molecular basis for polymer flammability. Polymer 2009, 50, 2608–2617. [Google Scholar] [CrossRef]
- Sonnier, R.; Negrell-Guirao, C.; Vahabi, H.; Otazaghine, B.; David, G.; Lopez-Cuesta, J.M. Relationships between the molecular structure and the flammability of polymers: Study of phosphonate functions using microscale combustion calorimeter. Polymer 2012, 53, 1258–1266. [Google Scholar] [CrossRef]
- Sonnier, R.; Otazaghine, B.; Iftene, F.; Negrell, C.; David, G.; Howell, B. Predicting the flammability of polymers from their chemical structure: An improved model based on group contributions. Polymer 2016, 86, 42–55. [Google Scholar] [CrossRef]
- Sonnier, R.; Otazaghine, B.; Dumazert, L.; Menard, R.; Viretto, A.; Dumas, L.; Bonnaud, L.; Dubois, P.; Safronava, N.; Walters, R.; et al. Prediction of thermosets flammability using a model based on group contributions. Polymer 2017, 127, 203–213. [Google Scholar] [CrossRef]
- Vyazaovkin, S. Model-free kinetics—Staying free of multiplying entities without necessity. J. Therm. Anal. Calorim. 2006, 83, 45–51. [Google Scholar]
- Brems, A.; Baeyens, J.; Beerlandt, J.; Dewil, R. Thermogravimetric pyrolysis of waste polyethylene-terephtalate and polystyrene: A critical assessment of kinetics modelling. Resour. Conserv. Recycl. 2011, 55, 772–781. [Google Scholar] [CrossRef]
- Aoyagi, Y.; Yamashita, K.; Doi, Y. Thermal degradation of poly[(R)-3-hydroxybutyrate], poly[ε-caprolactone], and poly[(S)-lactide]. Polym. Degrad. Stab. 2002, 76, 53–59. [Google Scholar] [CrossRef]
- Ariffin, H.; Nishida, H.; Shirai, Y.; Hasan, M.A. Determination of multiple thermal degradation mechanisms of poly(3-hydroxybutyrate). Polym. Degrad. Stab. 2008, 93, 1433–1439. [Google Scholar] [CrossRef]
- Kopinke, F.D.; Mackenzie, K. Mechanistic aspetcs of the thermal degradation of poly(lactic acid) and poly(β-hydroxybutyric acid). J. Anal. Appl. Pyrolysis 1997, 40–41, 43–53. [Google Scholar] [CrossRef]
- Kopinke, F.D.; Remmler, M.; Mackenzie, K. Thermal decomposition of biodegradable polyesters—II. Poly(β-hydroxybutyric acid). Polym. Degrad. Stab. 1996, 52, 25–38. [Google Scholar] [CrossRef]
- ASTM D7309-13. Standard Test Method for Determining Flammability Characteristics of Plastics and Other Solid Materials Using Microscale Combustion Calorimetry; American Society for Testing and Materials: West Conshocken, PA, USA, 2013. [Google Scholar]
- Sanchez-Jimenez, P.E.; Criado, J.M.; Perez-Maqueda, L.A. Kissinger kinetic analysis of data obtained under different heating schedules. J. Therm. Anal. Calorim. 2008, 94, 427–432. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Flynn, J.; Wall, L. General Treatment of the Thermogravimetry of Polymers. J. Res. Natl. Bur. Stand. A Phys. Chem. 1966, 70A, 487–523. [Google Scholar] [CrossRef]
- Li, J.; Zheng, W.; Li, L.; Zheng, Y.; Lou, X. Thermal degradation kinetics of g-HA/PLA composite. Thermochim. Acta 2009, 493, 90–95. [Google Scholar] [CrossRef]
- Ortega, A.; Perez Maqueda, L.; Criado, J.M. The problem of discerning Avrami-Erofeev kinetic models from the new controlled rate thermal analysis with constant acceleration of the transformation. Thermochim. Acta 1995, 254, 147–152. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Te Nijenhuis, K. Properties of Polymers, 4th ed.; Elsevier Science: Amsterdam, The Netherlands, 2009. [Google Scholar]












| Polymer | Manufacturer | Chemical structure | Heat of complete combustion (kJ/g) |
|---|---|---|---|
| (High density) Polyethylene | Eraclene FC 92 Polimeri Europa |  | 42 |
| Polypropylene | 3100 MT3 1P2381 Atofina |  | 39 |
| Polyethylene terephthalate | Arnite D04 300 |  | 16 |
| Polybutylene terephthalate | Valox 325F GE Plastics |  | 20 |
| Polycaprolactone | CAPA 6800 Perstorp |  | 26.5 |
| Polybutylene succinate | 2003F Xinfu Pharm |  | 21.5 |
| Poly(3-hydroxybutyrate) | Biocycle 1000 |  | 20 |
| Polylactic acid | Unitika 6201-D |  | 16 |
| Polyglycolide | Sigma Aldrich |  | 10.5 |
| Polymethyl methacrylate | Altuglas V825T |  | 23 |
| Polystyrene | Lacqrène 1340 Atofina |  | 35 |
| Polymer | Flynn-Wall-Ozawa method | Kissinger method | |||||
|---|---|---|---|---|---|---|---|
| Ea (kJ/mol) | Ea (kJ/mol) | LnA | |||||
| α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | Mean | |||
| PE | 210 | 217 | 210 | 209 | 211 | 221 | 29.2 |
| PP | 202 | 194 | 192 | 187 | 194 | 198 | 26.9 |
| PET | 169 | 177 | 182 | 193 | 180 | 180 | 24.7 |
| PBT | 157 | 163 | 165 | 172 | 164 | 174 | 25.6 |
| PCL | 139 | 163 | 166 | 172 | 160 | 151 | 21.3 |
| PBS | 125 | 140 | 148 | 151 | 141 | 154 | 21.8 |
| PHB | 98 | 93 | 89 | 84 | 91 | 91 | 15.4 |
| PLA | 109 | 100 | 116 | 120 | 111 | 126 | 18.2 |
| PG | 95 | 89 | 91 | 94 | 92 | 86 | 10.4 |
| PMMA | 164 | 170 | 174 | 193 | 175 | 176 | 27.4 |
| PS | 159 | 158 | 159 | 162 | 159 | 160 | 22.0 |
| Chemical groups | Mw (g/mol) | Contribution to | |
|---|---|---|---|
| Ea (kJ/mol) | LnA | ||
 | 14 | 220 | 29 |
 | 29 | 170 | 27 |
 | 76 | 280 | 38 |
 | 44 | 60 | 10 |
| Polymer | n |
|---|---|
| PE | 2 |
| PP | 1.5 |
| PET | 1.5 |
| PBT | 1.5 |
| PCL | 1.5 |
| PBS | 1.5 |
| PHB | 3.5 |
| PLA | 2 |
| PG | 2.5 |
| PMMA | 1 |
| PS | 2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumazert, L.; Sonnier, R. An Insight into the Flammability of Some Bio-Based Polyesters. Polymers 2017, 9, 706. https://doi.org/10.3390/polym9120706
Dumazert L, Sonnier R. An Insight into the Flammability of Some Bio-Based Polyesters. Polymers. 2017; 9(12):706. https://doi.org/10.3390/polym9120706
Chicago/Turabian StyleDumazert, Loïc, and Rodolphe Sonnier. 2017. "An Insight into the Flammability of Some Bio-Based Polyesters" Polymers 9, no. 12: 706. https://doi.org/10.3390/polym9120706
APA StyleDumazert, L., & Sonnier, R. (2017). An Insight into the Flammability of Some Bio-Based Polyesters. Polymers, 9(12), 706. https://doi.org/10.3390/polym9120706