A Parametric Model for Local Air Exchange Rate of Naturally Ventilated Barns
Abstract
:1. Introduction
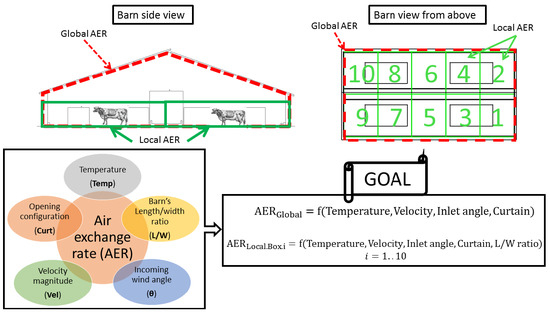
- Under the same boundary conditions, local AERs can show considerably different behavior, first, depending on the position inside the barn and second, in comparison with the global AER.
- The interaction between the temperature and velocity (which is directly related to the flow convection type) has a strong influence on the global and local AERs, as well as the interactions between other pre-cited parameters confirmed in previous studies.
2. Methodology and Materials
2.1. CFD Model
2.1.1. Domain and Boundary Condition
2.1.2. Numerical Solver and Mesh
2.2. Parameters
2.3. Simulation Scheme and Automatizing Details (with Ansys Fluent and Python)
2.4. AER Evaluation
2.5. Tools and Methods for Statistical Analysis (with R)
2.5.1. Principal Component Analysis
2.5.2. General Linear Model (GLM)
3. Results and Discussions
3.1. Clustering with PCA
3.2. AER Formulas
3.2.1. For the Whole Barn
- multiplied with produced high equation values. This means that the velocity magnitude has a strong impact on the increase in the AER.
- is negative, showing that with increasing temperature the AER tends to decrease. This effect is slightly dampened for the reduced opening configurations ().
- Another interesting observation is that the reduction in the opening decreases the AER. and are both negative and have the same magnitude as the intercept. This goes together with the observation of [10]. In his paper, he investigated the influence of several opening configurations on the flow pattern and the airflow rate of an NVDB for high-velocity magnitude at the 0 airflow direction. He also observed that the AER of the curtain Open Down is slightly less than the Open Up configuration. It is also consistent with the wind tunnel experiments of [26], who also reported a significant reduction in the AER when closing parts of the sidewall opening, where a lower air exchange was observed in the open-down case than in the open-up case. The same can be noted in our study when looking at how for the forced convection group (high velocity), which means that the higher the velocity, the more the AER is reduced for the Open Down curtain compared to the Open Up curtain. On the other hand, as > , for lower velocities (in this setting around 1 m/s), the air exchange in the open-up and open-down cases will be nearly equal, but still considerably reduced compared with the fully open case. The latter fits well with the observations in the wind tunnel experiments of [25].
- Changing in the incoming air inlet angle also reduced the AER ( is negative). This effect is even more accentuated for 90 inlet angle, since is around three times . This is also consistent with previous reports on the effect of wind incident angle [27,28]. However, when the opening is reduced, we observed an attenuation by the positivity of . The attenuation is not complete, since .
3.2.2. For the 10 Boxes Subdivision
- As in the general AER, the velocity magnitude ( at the beginning of the second row) has a strong effect on the increase in the . However, for the inlet angle is 45(), the effect is attenuated, especially at the upper half of the barn (boxes 5–10). For = 90 () the AER are decreased even more, but this time for the boxes of the rear half of the barn (boxes 2, 4, 6, 8, 10). We noted that the pattern of is approximately complementary to and also to : such a contrast slightly dampens the effect of . This is consistent with contemporary knowledge of the indoor air flow pattern of naturally ventilated cattle buildings. For example, [29] concluded, from on-farm measurements in the AOZ with 25 and 70 incident wind angle, that the speed and direction of the incident wind significantly influence the air velocity in the AOZ.
- Here, the temperature () decreases the (except at boxes 1 and 3), but the effect is more pronounced in the rear and upper half of the barn (boxes 2, 4, 6, 7, 8, 9, 10). This effect is the same for the reduced openings; see the last column, and .
- The similarity with the general AER continues. The coefficients for the curtain levels Open Down and Open Up (, , second row) are both negative, meaning that the reduced opening size reduces the local AER (OU more than OD, with stronger effects at the rear half of the barn). This goes together with the indoor air flow pattern observed by [17] wind tunnel experiments with different opening configurations. The study reported a slightly lower wind speed in the AOZ in the Open Down case compared to the open case and a considerably lower wind speed in the AOZ in the Open Up case compared to the Open case. While, in our study, the reduction effect on the local AER was generally stronger in the rear half of the barn, the changes in the air flow pattern reported by [17] were more pronounced in the front part of the barn. However, this difference might be explained by the fact that [17] considered only one cross-section through the building and a model with a L/W ratio of nearly 1:1.
- , , and (third and fourth columns from the left) allowed us to analyze the influence of inlet angle on the reduced opening configurations. We note that with increasing inlet angle, the coefficients also increase. For 45, the boxes 2, 4, 6 of the rear half and 7, 9 of front half are still negative, while their counterparts on the other side are positive. For 90, they all turn positive, with high values complementary to the original coefficient and . (Where there are high values of , we have low values of . The same applies to and .)
- Patterns for and can hardly be recognized. However, we noticed that the values switch from positive to negative (or high to low) from a box of one half-barn side (front or rear) to the other half-barn side, except for box 1 and 2, which have almost same values. An average over all the boxes gave a value near to zero. This might explain why the parameter has no significant impact on the general AER, since the local AERs compensate for each other.
- When interacts with the inlet angle (second and third columns from the right), we note that the patterns of are complementary to , and the ones of to . However, the magnitude of the is higher than the magnitude of the , especially for . This means that for a higher , increasing the inlet angle tends to create an opposite effect to that for smaller .
- Again, as for the general AER, the velocity magnitude ( at the beginning of the second row) has a significant effect on the increase in the . However, for the inlet angle 45 () the effect is attenuate. For = 90 (), are decreased, especially for the boxes of the rear half of the barn (boxes 2, 4, 6, 8, 10).
- Here, too, the temperature decreases the but the effect is more pronounced in the front half of the barn (boxes 1, 3, 5, 7, 9).
- The coefficients for curtain levels Open Down and Open Up (, , second row) are both negative, meaning that the reducing opening size reduces local AER (OD reduces more in the front half of the barn, except for box 1, with a pattern that is complementary to alpha).
- For , , and (second and third columns from the left), we note that with increasing inlet angle, the coefficients also increase. For 45, the boxes at the rear half of the barn (and for box 1), the coefficients are still negative, but for 90, they all turn positive. However, the lowest values are retained for the boxes in the rear half of the boxes and box 1.
- As in the forced convection case, the values of and vary between high and low from one half of the barn to the other. When the openings are reduced (), there are small changes in most of the boxes (light colors which means close to zero). The three boxes with high values (5, 7, 9) are complementary to their respective original .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NVDB | Naturally Ventilated Dairy Barn |
| AER | Air Exchange Rate |
| CFD | Computational Fluid Dynamics |
| RANS | Reynolds Averaged Navier-Stokes |
| CPU | Control Processing Unit |
| ER | Emission Rate |
| ABL | Atmospheric Boundary Layer |
| AOZ | Animal Occupied Zone |
| TUI | Text User Interface |
| PCA | Principal Component Analysis |
| RSE | Residual Standard Error |
| AIC | Akaike information criterion |
References
- Grethe, H.; Christen, O.; Balmann, A.; Bauhus, J.; Birner, R.; Bokelmann, W.; Gauly, M.; Knierim, U.; Latacz-Lohmann, U.; Nieberg, H.; et al. Wege zu Einer Gesellschaftlich Akzeptierten Nutztierhaltung. Ber. Landwirtsch. Z. Agrarpolit. Landwirtsch. 2015, 221, 1–171. [Google Scholar] [CrossRef]
- Beattie, V.; O’Connell, N.; Kilpatrick, D.; Moss, B. Influence of environmental enrichment on welfare-related behavioural and physiological parameters in growing pigs. Anim. Sci. 2000, 70, 443–450. [Google Scholar] [CrossRef]
- Umweltschutztechnik, F. Emissionen und Immissionen aus Tierhaltungsanlagen—Haltungsverfahren und Emissionen000Schweine, Rinder, Geflügel, Pferde; VDI/DIN: Berlin, Germany, 2011; p. 84. [Google Scholar]
- Samer, M.; Fiedler, M.; Müller, H.J.; Gläser, M.; Ammon, C.; Berg, W.; Sanftleben, P.; Brunsch, R. Winter measurements of air exchange rates using tracer gas technique and quantification of gaseous emissions from a naturally ventilated dairy barn. Appl. Eng. Agric. 2011, 27, 1015–1025. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W.; Grant, J.; Fallon, R.; Dodd, V. Applications of computational fluid dynamics (CFD) in the modelling and design of ventilation systems in the agricultural industry: A review. Bioresour. Technol. 2007, 98, 2386–2414. [Google Scholar] [CrossRef]
- Bartzanas, T.; Boulard, T.; Kittas, C. Numerical simulation of the airflow and temperature patterns in a greenhouse equipped with insect-proof screen in the openings. Comput. Electron. Agric. 2002, 34, 207–221. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002; p. 364. [Google Scholar] [CrossRef]
- Bartzanas, T.; Kacira, M.; Zhu, H.; Karmakar, S.; Tamimi, E.; Katsoulas, N.; Lee, I.B.; Kittas, C. Computational fluid dynamics applications to improve crop production systems. Comput. Electron. Agric. 2013, 93, 151–167. [Google Scholar] [CrossRef]
- Lee, I.; Bitog, J.P.; Hong, S.W.; Seo, I.; Kwon, K.; Bartzanas, T.; Kacira, M. The past, present and future of CFD for agro-environmental applications. Comput. Electron. Agric. 2013, 93, 168–183. [Google Scholar] [CrossRef]
- Saha, C.K.; Yi, Q.; Janke, D.; Hempel, S.; Amon, B.; Amon, T. Opening Size Effects on Airflow Pattern and Airflow Rate of a Naturally Ventilated Dairy Building—A CFD Study. Appl. Sci. 2020, 10, 6054. [Google Scholar] [CrossRef]
- Doumbia, M.; Hempel, S.; Janke, D.; Amon, T. Prediction of the Local Air Exchange Rate in Animal Occupied Zones of a Naturally Ventilated Barn. In Proceedings of the Sustainable Decisions in Bio-Economy (CIOSTA 2019)—XXXVIII CIOSTA & CIGR V International Conference, Rhodes, Greece, 24–26 June 2019; pp. 29–34. [Google Scholar]
- Yi, Q.; Zhang, G.; Amon, B.; Hempel, S.; Janke, D.; Saha, C.; Amon, T. Modelling air change rate of naturally ventilated dairy buildings using response surface methodology and numerical simulation. Build. Simul. 2020, 14, 827–839. [Google Scholar] [CrossRef]
- Doumbia, E.M.; Janke, D.; Yi, Q.; Amon, T.; Kriegel, M.; Hempel, S. CFD modelling of an animal occupied zone using an anisotropic porous medium model with velocity depended resistance parameters. Comput. Electron. Agric. 2021, 181, 105950. [Google Scholar] [CrossRef]
- Janke, D.; Caiazzo, A.; Ahmed, N.; Alia, N.; Knoth, O.; Moreau, B.; Wilbrandt, U.; Willink, D.; Amon, T.; John, V. On the feasibility of using open source solvers for the simulation of a turbulent air flow in a dairy barn. Comput. Electron. Agric. 2020, 175, 105546. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Betriebe Milchkuhhaltung nach Bestandsgrößenklassen. Ergebnisse der repräsentativen Agrarberichterstattung (Vorläufig). 1993.
- Yi, Q.; König, M.; Janke, D.; Hempel, S.; Zhang, G.; Amon, B.; Amon, T. Wind tunnel investigations of sidewall opening effects on indoor airflows of a cross-ventilated dairy building. Energy Build. 2018, 175, 163–172. [Google Scholar] [CrossRef]
- Gebremedhin, K.; Wu, B. Simulation of flow field of a ventilated and occupied animal space with different inlet and outlet conditions. J. Therm. Biol. 2005, 30, 343–353. [Google Scholar] [CrossRef]
- Saha, C.; Fiedler, M.; Ammon, C.; Berg, W.; Loebsin, C.; Amon, B.; Amon, T. Uncertainty in calculating air exchange rate of naturally ventilated dairy building based on point concentrations. Environ. Eng. Manag. J. 2014, 13, 2349–2355. [Google Scholar] [CrossRef]
- Marek, R.; Nitsche, K. Praxis der Wärmeübertragung Grundlagen—Anwendungen—Übungsaufgaben, 4., neu bearbeitete auflage ed.; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2015; p. 343. [Google Scholar]
- Wang, X.; Zhang, G.; Choi, C.Y. Evaluation of a precision air-supply system in naturally ventilated freestall dairy barns. Biosyst. Eng. 2018, 175, 1–15. [Google Scholar] [CrossRef]
- Saha, C.; Fiedler, A.; Amon, T.; Berg, W.; Amon, B.; Brunsch, R. Assessing effects of different opening combinations on airflow pattern and air exchange rate of a naturally ventilated dairy building—A CFD approach. In Proceedings of the International Conference of Agricultural Engineering AgEng, Zurich, Switzerland, 6–10 July 2014. [Google Scholar]
- Mondaca, M.R.; Choi, C.Y. Assessment of Dairy Cow Geometries in Computational Modeling. In Proceedings of the 2015 ASABE Annual International Meeting, Chicago, IL, USA, 3–5 May 2015. [Google Scholar]
- Dalgaard, P. Introductory Statistics with R, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; p. 364. [Google Scholar]
- Shen, X.; Su, R.; Ntinas, G.K.; Zhang, G. Influence of sidewall openings on air change rate and airflow conditions inside and outside low-rise naturally ventilated buildings. Energy Build. 2016, 130, 453–464. [Google Scholar] [CrossRef]
- Paepe, M.D.; Pieters, J.G.; Cornelis, W.M.; Gabriels, D.; Merci, B.; Demeyer, P. Airflow measurements in and around scale model cattle barns in a wind tunnel: Effect of ventilation opening height. Biosyst. Eng. 2012, 113, 22–32. [Google Scholar] [CrossRef]
- Paepe, M.D.; Pieters, J.G.; Cornelis, W.M.; Gabriels, D.; Merci, B.; Demeyer, P. Airflow measurements in and around scale-model cattle barns in a wind tunnel: Effect of wind incidence angle. Biosyst. Eng. 2013, 115, 211–219. [Google Scholar] [CrossRef]
- Rong, L.; Liu, D.; Pedersen, E.; Zhang, G. The effect of wind speed and direction and surrounding maize on hybrid ventilation in a dairy cow building in Denmark. Energy Build. 2015, 86, 25–34. [Google Scholar] [CrossRef]
- Fiedler, M.; Berg, W.; Ammon, C.; Loebsin, C.; Sanftleben, P.; Samer, M.; von Bobrutzki, K.; Kiwan, A.; Saha, C.K. Air velocity measurements using ultrasonic anemometers in the animal zone of a naturally ventilated dairy barn. Biosyst. Eng. 2013, 116, 276–285. [Google Scholar] [CrossRef]










| Inflow Direction | North Side | South Side | West Side | East Side |
|---|---|---|---|---|
| 0 | velocity inlet | pressure outlet | Wall | Wall |
| 45 | velocity inlet | pressure outlet | velocity inlet | pressure outlet |
| 90 | Wall | wall | velocity inlet | pressure outlet |
| Ri Cases | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Type of Convection | Forced | Mixed | Natural | ||||||
| Ri domain | Ri < 0.2 | 0.2 < Ri < 5 | Ri > 5 | ||||||
| Ri values | Ri = 0.048 | Ri = 0.078 | Ri = 0.198 | Ri = 0.8 | Ri = 1.9 | Ri = 3 | Ri = 12 | Ri = 28 | Ri = 51.75 |
| T (C) | 32 | 30 | 22 | 18 | 15 | 10 | 7 | 0 | −2 |
| U (m s) | 3.2 | 2.8 | 2.5 | 1.4 | 0.97 | 0.85 | 0.45 | 0.33 | 0.25 |
| Season | Summer | Fall-Spring | Winter | ||||||
| Parameter Description | Velocity Magnitude | Ambient Temperature | Inlet Angle | Width/Length Barn Ratio | Curtain Position |
|---|---|---|---|---|---|
| Variable Type | Continuous | Continuous | Factor | Factor | Factor |
| Standard | - | - | 0 | LW2 | Total open |
| Cluster Group | Coefficients | RSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| All | 40.25 | −1.42 | 61.98 | OU | −19.06 | −32.81 | 0.54 | 45 | −12.32 | 4.58 | 0.98 |
| OD | −12.85 | −39.09 | 0.84 | 90 | −44.94 | ||||||
| Nat-Mix | 43.83 | −1.01 | 50.87 | OU | −20.25 | −29.07 | 0.33 | 45 | −17.17 | 3.31 | 0.96 |
| OD | −12.85 | −28.74 | 0.58 | 90 | −36.47 | ||||||
| Forced | 36.99 | −0.76 | 56.92 | OD | −25.86 | −30.00 | 0.50 | 45 | −11.53 | 4.04 | 0.99 |
| OU | −5.06 | −34.96 | 0.09 | 90 | −46.33 | ||||||
| Cluster Group | Coefficients | |||
|---|---|---|---|---|
| All | 5.10 | 26.65 | 10.16 | 30.50 |
| Nat-Mix | 10.35 | 22.85 | 11.00 | 20.22 |
| Forced | 4.23 | 27.27 | 10.02 | 32.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doumbia, E.M.; Janke, D.; Yi, Q.; Prinz, A.; Amon, T.; Kriegel, M.; Hempel, S. A Parametric Model for Local Air Exchange Rate of Naturally Ventilated Barns. Agronomy 2021, 11, 1585. https://doi.org/10.3390/agronomy11081585
Doumbia EM, Janke D, Yi Q, Prinz A, Amon T, Kriegel M, Hempel S. A Parametric Model for Local Air Exchange Rate of Naturally Ventilated Barns. Agronomy. 2021; 11(8):1585. https://doi.org/10.3390/agronomy11081585
Chicago/Turabian StyleDoumbia, E. Moustapha, David Janke, Qianying Yi, Alexander Prinz, Thomas Amon, Martin Kriegel, and Sabrina Hempel. 2021. "A Parametric Model for Local Air Exchange Rate of Naturally Ventilated Barns" Agronomy 11, no. 8: 1585. https://doi.org/10.3390/agronomy11081585
APA StyleDoumbia, E. M., Janke, D., Yi, Q., Prinz, A., Amon, T., Kriegel, M., & Hempel, S. (2021). A Parametric Model for Local Air Exchange Rate of Naturally Ventilated Barns. Agronomy, 11(8), 1585. https://doi.org/10.3390/agronomy11081585