GABA Receptors Can Depolarize the Neuronal Membrane Potential via Quantum Tunneling of Chloride Ions: A Quantum Mathematical Study
Abstract
:1. Introduction
2. Materials and Methods
The Mathematical Model of Chloride Ions Quantum Tunneling
3. Results
3.1. The Quantum Tunneling Probability of Chloride Ions through the Closed GABA Receptors
3.2. The Quantum Unitary Conductance of Closed GABA Receptors Mediated by the Quantum Tunneling of Chloride Ions
3.3. The Quantum Membrane Conductance from the Closed GABA Receptors
3.4. The Quantum Tunneling-Induced Membrane Depolarization via Quantum Tunneling of Chloride Ions through the Closed GABA Receptors
3.5. The Effect of the Intracellular Chloride Concentration on the Resting Membrane Potential Based on the Quantum and Classical Models
4. Discussion
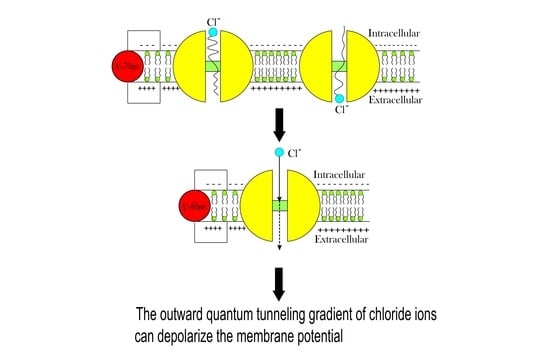
- It is clear that the tunneling probability of intracellular chloride ions is higher than that of extracellular chloride ions. This is attributed to the difference in the kinetic energy when they reach the closed gate. The higher the kinetic energy, the higher the tunneling probability. As the membrane potential is negative inside with regard to outside, it is expected that the intracellular chloride ion acquires kinetic energy while passing in GABA receptor until hitting the closed gate, while the extracellular chloride ions will lose kinetic energy as they pass in GABA receptors until reaching the closed gate. See Figure 20.
- 2.
- The tunneling probability of both intracellular and extracellular chloride ions decreases as the energy of the gate and the length of the gate increase. On the other hand, the membrane potential has a differential effect on chloride ions. As the membrane potential increases, the tunneling probability of intracellular chloride ions increases, whereas the tunneling probability of extracellular chloride ions decreases as the membrane potential increases. Additionally, as the value of n increases, the membrane potential available for intracellular chloride ions increases and thus their tunneling probability increases. However, as the value of n increases, the membrane potential opposing the movement of extracellular chloride ions and the loss of their kinetic energy decrease and thus their tunneling probability increases.
- According to the quantum tunneling model, the quantum unitary conductance of the intracellular chloride ions is higher than the quantum conductance of the extracellular chloride ions. On the other hand, the classical model assigns the same unitary conductance for both extracellular and intracellular chloride ions.
- If we take the classical unitary conductance of open GABA receptor to be 30 × 10−12 S [32], it seems obvious that the quantum unitary conductance is extremely small until reaching near G = 2 J, at which the quantum unitary conductance becomes comparable to the classical value. Therefore, it is expected that the quantum tunneling of chloride ions becomes influential when the energy of the gate of GABA receptors decreases to 2 J or less, as will be explained later in the paper. Based on the quantum tunneling model, it is predicted that GABA receptors have persistent basal activity in the absence of GABA ligands under certain conditions that can be physiological or pathological if they cause a decrease in the energy of the closed gate. The quantum tunneling effect will be extremely low at gate energy values higher than 2 J.
- The quantum unitary conductance changes according to the energy of the gate, the length of the gate, the membrane potential, and the location of the gate as it was discussed regarding the tunneling probability.
- The quantum membrane conductance of intracellular chloride ions is higher than the quantum membrane conductance of the extracellular chloride ions. This discrepancy in the quantum conductance will result in a net efflux of chloride ions.
- If the quantum conductance values are compared with the leaky classical conductance values of potassium and sodium ions at the resting state, which are 0.5 mS/cm2 and 0.022 mS/cm2, then it is clear that the values of quantum conductance for the intracellular ions become comparable to the classical ones once the energy of the closed gate drops to 2 J. This is said to provide an empirical prediction regarding the influence of quantum tunneling on the resting membrane potential. As the quantum conductance of the extracellular ions remain extremely low across all different values of gate energy and the quantum conductance of the intracellular ions becomes comparable to the leaky conductance of sodium and potassium ions around G = 2 J, then it is expected that chloride ions can depolarize the resting membrane potential via quantum tunneling through the closed GABA receptors.
4.1. The Influence of Chloride Ions Quantum Tunneling on the Resting Membrane Potential
4.1.1. The Influence of Quantum Tunneling of Chloride Ions at Different Values of Gate Length L
4.1.2. The Influence of Quantum Tunneling of Chloride Ions at Different Values of Gate Location n
4.1.3. The Influence of Quantum Tunneling of Chloride Ions on the Resting Membrane Potential at Different Values of Channels Density D
4.2. The Comparison between the Classical and Quantum Models of GABA Receptors in Terms of the Intracellular Chloride Concentration
4.3. Possible Proposed Mechanisms behind the Drop in the Energy of the Closed Gate of GABA Receptors and Potential Implications and Perspectives
- We propose that during early development, the binding of GABA ligand to its receptor does not yield the full activation energy needed to open the closed gate; hence, the gate remains closed but with less energy barrier than before. Accordingly, the quantum tunneling of the intracellular chloride ions will be augmented more significantly than the tunneling of the extracellular chloride ions. This yields a quantum gradient that produces a net chloride efflux that leads to membrane depolarization, which has been observed during early neuronal development [2,3,4].
- The gain-of-function mutations are well-established genetic conditions that affect ion channels such as ligand-gated channels and voltage-gated channels [33,34]. If these gain-of-function mutations decrease the gate energy of the closed GABA receptor, this will enhance the quantum tunneling of chloride ions to depolarize the membrane potential. Interestingly, this quantum tunneling-induced membrane depolarization occurs even without GABA binding to the receptor because the drop of the gate energy had occurred. Therefore, these mutations may be responsible for generating outward anion current that depolarizes membrane potential, which explains the increased tendency of seizures in patients with such mutations [33,34].
- Acquired conditions such as stroke and trauma are implicated as pathological events that affect the function of GABA receptors [5,6]. As such conditions can decrease the energy required to open the voltage-gated channels [35,36], this can be extrapolated and applied on GABA receptors because they share the same hydrophobic gating mechanism [14,17]. Accordingly, these conditions can decrease the energy of the closed gate in GABA receptors, which leads to enhancing the quantum tunneling of chloride ions.
- Since the depolarization mediated by GABA receptors can result in excitatory effects or inhibitory effects [8], this idea can be used to explain the mechanism of action of certain classes of agents and medications. These agents include the anesthetic agents that are used to shut down the consciousness so that certain surgery can be done. The classical view is that these agents activate the GABA receptors to induce hyperpolarizing currents and thus decrease neuronal activity [37,38]. In the perspective of the quantum tunneling model, these agents can hypothetically be viewed as quantum tunneling enhancers by lowering the values of gate energy facilitating the chloride efflux, which leads to quantum tunneling-induced membrane depolarization. This depolarization may inhibit neuronal activity, which explains the anesthetic effects of these agents. Moreover, the quantum tunneling model predicts the ability of chloride ions to depolarize the membrane potential by a large degree, reaching less than 10 mV (negative inside with regard to outside), as is clearly evident in Figure 14, Figure 15, Figure 16 and Figure 17. This large depolarization significantly increases the fraction of the inactivated sodium channels blocking the neuronal activity even though that membrane potential is depolarized, and this can be served to explain the inhibitory effects of anesthetic agents on consciousness.
- Interestingly, as the quantum tunneling model predicts the ability of GABA receptor to permeate chloride ions without the binding of GABA ligand at certain range of gate energy, this comes consistent with the spontaneous activity of GABA receptors without the requirement of GABA binding, which has been observed and mentioned in the literature [39].
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Spitzer, N.C. How GABA generates depolarization. J. Physiol. 2010, 588, 757. [Google Scholar] [CrossRef] [PubMed]
- Ben-Ari, Y.E.; Cherubini, E.N.; Corradetti, R.E.; Gaiarsa, J. Giant synaptic potentials in immature rat CA3 hippocampal neurons. J. Physiol. 1989, 416, 303–325. [Google Scholar] [CrossRef] [PubMed]
- Kasyanov, A.M.; Safiulina, V.F.; Voronin, L.L.; Cherubini, E. GABA-mediated giant depolarizing potentials as coincidence detectors for enhancing synaptic efficacy in the developing hippocampus. Proc. Natl. Acad. Sci. USA 2004, 101, 3967–3972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fritschy, J.M. Epilepsy, E/I balance and GABAA receptor plasticity. Front. Mol. Neurosci. 2008, 1, 5. [Google Scholar] [CrossRef] [Green Version]
- Jaenisch, N.; Witte, O.W.; Frahm, C. Downregulation of potassium chloride cotransporter KCC2 after transient focal cerebral ischemia. Stroke 2010, 41, e151–e159. [Google Scholar] [CrossRef]
- Dzhala, V.; Valeeva, G.; Glykys, J.; Khazipov, R.; Staley, K. Traumatic alterations in GABA signaling disrupt hippocampal network activity in the developing brain. J. Neurosci. 2012, 32, 4017–4031. [Google Scholar] [CrossRef]
- Herbison, A.E.; Moenter, S.M. Depolarising and hyperpolarising actions of GABAA receptor activation on GnRH neurons: Towards an emerging consensus. J. Neuroendocrinol. 2011, 23, 557. [Google Scholar] [CrossRef] [Green Version]
- Kilb, W. When Are Depolarizing GABAergic Responses Excitatory? Front. Mol. Neurosci. 2021, 14, 747835. [Google Scholar] [CrossRef]
- Khreesha, L.; Qaswal, A.B.; Al Omari, B.; Albliwi, M.A.; Ababneh, O.; Albanna, A.; Abunab’ah, A.; Iswaid, M.; Alarood, S.; Guzu, H.; et al. Quantum Tunneling-Induced Membrane Depolarization Can Explain the Cellular Effects Mediated by Lithium: Mathematical Modeling and Hypothesis. Membranes 2021, 11, 851. [Google Scholar] [CrossRef]
- Alrabayah, M.; Qaswal, A.B.; Suleiman, A.; Khreesha, L. Role of Potassium Ions Quantum Tunneling in the Pathophysiology of Phantom Limb Pain. Brain Sci. 2020, 10, 241. [Google Scholar] [CrossRef] [Green Version]
- Qaswal, A.B.; Suleiman, A.; Guzu, H.; Harb, T.; Atiyat, B. The potential role of lithium as an antiviral agent against SARS-CoV-2 via membrane depolarization: Review and hypothesis. Sci. Pharm. 2021, 89, 11. [Google Scholar] [CrossRef]
- Qaswal, A.B. Quantum tunneling of ions through the closed voltage-gated channels of the biological membrane: A mathematical model and implications. Quantum Rep. 2019, 1, 19. [Google Scholar] [CrossRef] [Green Version]
- Qaswal, A.B.; Ababneh, O.; Khreesha, L.; Al-Ani, A.; Suleihat, A.; Abbad, M. Mathematical Modeling of Ion Quantum Tunneling Reveals Novel Properties of Voltage-Gated Channels and Quantum Aspects of Their Pathophysiology in Excitability-Related Disorders. Pathophysiology 2021, 28, 10. [Google Scholar] [CrossRef]
- Aryal, P.; Sansom, M.S.; Tucker, S.J. Hydrophobic gating in ion channels. J. Mol. Biol. 2015, 427, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Bali, M.; Akabas, M.H. The location of a closed channel gate in the GABAA receptor channel. J. Gen. Physiol. 2007, 129, 145–159. [Google Scholar] [CrossRef] [Green Version]
- Naffaa, M.M.; Hung, S.; Chebib, M.; Johnston, G.A.; Hanrahan, J.R. GABA-ρ receptors: Distinctive functions and molecular pharmacology. Br. J. Pharmacol. 2017, 174, 1881–1894. [Google Scholar] [CrossRef] [Green Version]
- Rao, S.; Klesse, G.; Lynch, C.I.; Tucker, S.J.; Sansom, M.S. Molecular Simulations of Hydrophobic Gating of Pentameric Ligand Gated Ion Channels: Insights into Water and Ions. J. Phys. Chem. B 2021, 125, 981–994. [Google Scholar] [CrossRef]
- Beckstein, O.; Sansom, M.S. A hydrophobic gate in an ion channel: The closed state of the nicotinic acetylcholine receptor. Phys. Biol. 2006, 3, 147. [Google Scholar] [CrossRef]
- Tepper, H.L.; Voth, G.A. Mechanisms of passive ion permeation through lipid bilayers: Insights from simulations. J. Phys. Chem. B 2006, 110, 21327–21337. [Google Scholar] [CrossRef] [Green Version]
- Khavrutskii, I.V.; Gorfe, A.A.; Lu, B.; McCammon, J.A. Free energy for the permeation of Na+ and Cl− ions and their ion-pair through a zwitterionic dimyristoyl phosphatidylcholine lipid bilayer by umbrella integration with harmonic fourier beads. J. Am. Chem. Soc. 2009, 131, 1706–1716. [Google Scholar] [CrossRef] [Green Version]
- Jia, Z.; Yazdani, M.; Zhang, G.; Cui, J.; Chen, J. Hydrophobic gating in BK channels. Nat. Commun. 2018, 9, 3408. [Google Scholar] [CrossRef] [PubMed]
- Xin, Y.; Huang, A.; Hu, Q.; Shi, H.; Wang, M.; Xiao, Z.; Zheng, X.; Di, Z.; Chu, P.K. Barrier Reduction of Lithium Ion Tunneling through Graphene with Hybrid Defects: First-Principles Calculations. Adv. Theory Simul. 2018, 1, 1700009. [Google Scholar] [CrossRef]
- Poltavsky, I.; Zheng, L.; Mortazavi, M.; Tkatchenko, A. Quantum tunneling of thermal protons through pristine graphene. J. Chem. Phys. 2018, 148, 204707. [Google Scholar] [CrossRef] [PubMed]
- Serway, R.A.; Moses, C.J.; Moyer, C.A. Modern Physics; Cengage Learning: Boston, MA, USA, 2004. [Google Scholar]
- Chen, F.; Hihath, J.; Huang, Z.; Li, X.; Tao, N.J. Measurement of single-molecule conductance. Annu. Rev. Phys. Chem. 2007, 58, 535–564. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bertil, H.; Bertil, H. Ion Channels of Excitable Membranes, 3rd ed.; Sinauer Associates: Sunderland, MA, USA, 2007; Volume 2001. [Google Scholar]
- Qaswal, A.B. Quantum Electrochemical Equilibrium: Quantum Version of the Goldman–Hodgkin–Katz Equation. Quantum Rep. 2020, 2, 17. [Google Scholar] [CrossRef]
- Jones, M.V.; Jonas, P.; Sahara, Y.; Westbrook, G.L. Microscopic kinetics and energetics distinguish GABAA receptor agonists from antagonists. Biophys. J. 2001, 81, 2660–2670. [Google Scholar] [CrossRef] [Green Version]
- Moran, L.A.; Horton, R.A.; Scrimgeour, K.G.; Perry, M.D. Principles of Biochemistry; Pearson: London, UK, 2014. [Google Scholar]
- Lodish, H.; Berk, A.; Kaiser, C.A.; Krieger, M.; Scott, M.P.; Bretscher, A.; Ploegh, H.; Matsudaira, P. Molecular Cell Biology; Macmillan: London, UK, 2008. [Google Scholar]
- Martín-Belmonte, A.; Aguado, C.; Alfaro-Ruíz, R.; Moreno-Martínez, A.E.; De La Ossa, L.; Martínez-Hernández, J.; Buisson, A.; Shigemoto, R.; Fukazawa, Y.; Luján, R. Density of GABAB receptors is reduced in granule cells of the hippocampus in a mouse model of Alzheimer’s disease. Int. J. Mol. Sci. 2020, 21, 2459. [Google Scholar] [CrossRef] [Green Version]
- Eghbali, M.; Birnir, B.; Gage, P.W. Conductance of GABAA channels activated by pentobarbitone in hippocampal neurons from newborn rats. J. Physiol. 2003, 552, 13–22. [Google Scholar] [CrossRef]
- Ahring, P.K.; Liao, V.W.; Gardella, E.; Johannesen, K.M.; Krey, I.; Selmer, K.K.; Stadheim, B.F.; Davis, H.; Peinhardt, C.; Koko, M.; et al. Gain-of-function variants in GABRD reveal a novel pathway for neurodevelopmental disorders and epilepsy. Brain J. Neurol. 2021, 144, awab391. [Google Scholar] [CrossRef]
- Crunelli, V.; Di Giovanni, G.; Parri, H.R.; Errington, A.C. Gain-of-function of thalamic extrasynaptic GABA-A receptors in typical absence seizures. In Extrasynaptic GABAA Receptors; Springer: New York, NY, USA, 2014; pp. 223–237. [Google Scholar]
- Morris, C.E. Voltage-gated channel mechanosensitivity: Fact or friction? Front. Physiol. 2011, 2, 25. [Google Scholar] [CrossRef] [Green Version]
- Reeves, D.; Ursell, T.; Sens, P.; Kondev, J.; Phillips, R. Membrane mechanics as a probe of ion-channel gating mechanisms. Phys. Rev. E 2008, 78, 041901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolfe, R.C. Inhaled anesthetic agents. J. PeriAnesthesia Nurs. 2020, 35, 441–444. [Google Scholar] [CrossRef] [PubMed]
- Son, Y. Molecular mechanisms of general anesthesia. Korean J. Anesthesiol. 2010, 59, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Neill, N.; Sylantyev, S. The functional role of spontaneously opening GABAA receptors in neural transmission. Front. Mol. Neurosci. 2019, 12, 72. [Google Scholar] [CrossRef]





















| L = 1 m | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 2.35 J | 0.0064 V | 0.046 V/J |
| L = 1.5 m | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 1.98 J | 0.0044 V | 0.066 V/J |
| L = 2 m | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 1.8 J | 0.0039 V | 0.081 V/J |
| n = 1 | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 1.2 J | 0.0062 V | 0.31 V/J |
| n = 2 | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 1.98 J | 0.0044 V | 0.066 V/J |
| n = 3 | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 2.23 J | 0.004 V | 0.053 V/J |
| D = 109 channels/cm2 | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 1.91 J | 0.0044 V | 0.071 V/J |
| D = 1010 channels/cm2 | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 1.98 J | 0.0044 V | 0.066 V/J |
| D = 1011 channels/cm2 | |||
| Ion | Gcur | Vm at G = 1 J | R |
| Cl | 2.05 J | 0.0044 V | 0.062 V/J |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawafleh, S.; Qaswal, A.B.; Suleiman, A.; Alali, O.; Zayed, F.M.; Al-Adwan, M.A.O.; Bani Ali, M. GABA Receptors Can Depolarize the Neuronal Membrane Potential via Quantum Tunneling of Chloride Ions: A Quantum Mathematical Study. Cells 2022, 11, 1145. https://doi.org/10.3390/cells11071145
Nawafleh S, Qaswal AB, Suleiman A, Alali O, Zayed FM, Al-Adwan MAO, Bani Ali M. GABA Receptors Can Depolarize the Neuronal Membrane Potential via Quantum Tunneling of Chloride Ions: A Quantum Mathematical Study. Cells. 2022; 11(7):1145. https://doi.org/10.3390/cells11071145
Chicago/Turabian StyleNawafleh, Sager, Abdallah Barjas Qaswal, Aiman Suleiman, Obada Alali, Fuad Mohammed Zayed, Mohammad Abu Orabi Al-Adwan, and Mo’ath Bani Ali. 2022. "GABA Receptors Can Depolarize the Neuronal Membrane Potential via Quantum Tunneling of Chloride Ions: A Quantum Mathematical Study" Cells 11, no. 7: 1145. https://doi.org/10.3390/cells11071145
APA StyleNawafleh, S., Qaswal, A. B., Suleiman, A., Alali, O., Zayed, F. M., Al-Adwan, M. A. O., & Bani Ali, M. (2022). GABA Receptors Can Depolarize the Neuronal Membrane Potential via Quantum Tunneling of Chloride Ions: A Quantum Mathematical Study. Cells, 11(7), 1145. https://doi.org/10.3390/cells11071145