How Can the International Monitoring System Infrasound Network Contribute to Gravity Wave Measurements?
Abstract
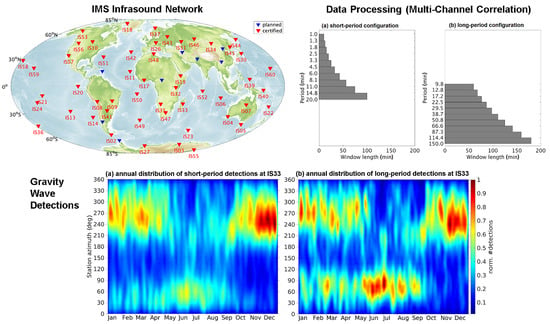
:1. Introduction
2. Processing
3. Results
3.1. A Global Dataset of Gravity Wave Detections
3.2. Gravity Wave Detections at Tropical Stations
3.3. Gravity Wave Detections near a Mid-Latitude Hotspot of Orographic GWs
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


References
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Holton, J.R. The Influence of Gravity Wave Breaking on the General Circulation of the Middle Atmosphere. J. Atmos. Sci. 1983, 40, 2497–2507. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics, 1st ed.; Academic Press: San Diego, CA, USA, 1982. [Google Scholar]
- Baldwin, M.P.; Dunkerton, P.J. Stratospheric Harbingers of Anomalous Weather Regimes. Science 2001, 294, 581–584. [Google Scholar] [CrossRef] [PubMed]
- Charlton-Perez, A.J.; Baldwin, M.P.; Birner, T.; Black, R.X.; Butler, A.H.; Calvo, N.; Davis, N.A.; Gerber, E.P.; Gillett, N.; Hardiman, S.; et al. On the lack of stratospheric dynamical variability in low-top versions of the CMIP5 models. J. Geophys. Res. 2013, 118, 2494–2505. [Google Scholar] [CrossRef]
- Geller, M.A.; Alexander, M.J.; Love, P.T.; Bacmeister, J.; Ern, M.; Hertzog, A.; Manzini, E.; Preusse, P.; Sato, K.; Scaife, A.A.; et al. Comparison between gravity wave momentum fluxes in observations and climate models. J. Clim. 2013, 26, 6383–6405. [Google Scholar] [CrossRef]
- Baumgarten, G. Doppler Rayleigh/Mie/Raman lidar for wind and temperature measurements in the middle atmosphere up to 80 km. Atmos. Meas. Tech. 2010, 3, 1509–1518. [Google Scholar] [CrossRef] [Green Version]
- Ern, M.; Trinh, Q.T.; Preusse, P.; Gille, J.C.; Mlynczak, M.G.; Russell, J.M., III; Riese, M. GRACILE: A comprehensive climatology of atmospheric gravity wave parameters based on satellite limb soundings. Earth Syst. Sci. Data 2018, 10, 857–892. [Google Scholar] [CrossRef]
- Hoffmann, L.; Xue, X.; Alexander, M.J. A global view of stratospheric gravity wave hotspots located with Atmospheric Infrared Sounder observations. J. Geophys. Res. 2013, 118, 416–434. [Google Scholar] [CrossRef] [Green Version]
- Preusse, P.; Eckermann, S.D.; Ern, M. Transparency of the atmosphere to short horizontal wavelength gravity waves. J. Geophys. Res. 2008, 113, D24104. [Google Scholar] [CrossRef]
- Rapp, M.; Dörnbrack, A.; Kaifler, B. An intercomparison of stratospheric gravity wave potential energy densities from METOP GPS radio occultation measurements and ECMWF model data. Atmos. Meas. Tech. 2018, 11, 1031–1048. [Google Scholar] [CrossRef] [Green Version]
- Ehard, B.; Kaifler, B.; Kaifler, N.; Rapp, M. Evaluation of methods for gravity wave extraction from middle-atmospheric lidar temperature measurements. Atmos. Meas. Tech. 2015, 8, 4645–4655. [Google Scholar] [CrossRef] [Green Version]
- Blanc, E.; Farges, T.; Le Pichon, A.; Heinrich, P. Ten year observations of gravity waves from thunderstorms in Western Africa. J. Geophys. Res. Atmos. 2014, 119, 6409–6418. [Google Scholar] [CrossRef]
- Marty, J.; Ponceau, D.; Dalaudier, F. Using the International Monitoring System infrasound network to study gravity waves. Geophys. Res. Lett. 2010, 37, L19802. [Google Scholar] [CrossRef]
- De Groot-Hedlin, C.D.; Hedlin, M.A.H.; Hoffmann, L.; Alexander, M.J.; Stephan, C.C. Relationships between gravity waves observed at earth’s surface and in the stratosphere over the Central and Eastern United States. J. Geophys. Res. Atmos. 2017, 122, 11482–11498. [Google Scholar] [CrossRef]
- Marlton, G.; Charlton-Perez, A.; Harrison, R.G.; Lee, C. Calculating Atmospheric Gravity Wave Parameters from Infrasound Measurements. In Infrasound Monitoring for Atmospheric Studies—Challenges in Middle-atmosphere Dynamics and Societal Benefits, 2nd ed.; Le Pichon, A., Blanc, E., Hauchecorne, A., Eds.; Springer: Dordrecht, The Netherlands, 2019; pp. 701–718. ISBN 978-3-319-75138-2. [Google Scholar] [CrossRef]
- Cansi, Y. An automatic seismic event processing for detection and location: The P.M.C.C. Method. Geophys. Res. Lett. 1995, 22, 1021–1024. [Google Scholar] [CrossRef]
- Le Pichon, A.; Matoza, R.; Brachet, N.; Cansi, Y. Recent Enhancements of the PMCC Infrasound Signal Detector. Inframatics 2010, 26, 5–8. [Google Scholar]
- Christie, D.R.; Campus, P. The IMS Infrasound Network: Design and Establishment of Infrasound Stations. In Infrasound Monitoring for Atmospheric Studies; Le Pichon, A., Blanc, E., Hauchecorne, A., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 29–75. ISBN 978-1-4020-9508-5. [Google Scholar] [CrossRef]
- Ceranna, L.; Matoza, R.S.; Hupe, P.; Le Pichon, A.; Landès, M. Systematic Array Processing of a Decade of Global IMS Infrasound Data. In Infrasound Monitoring for Atmospheric Studies—Challenges in Middle-atmosphere Dynamics and Societal Benefits, 2nd ed.; Le Pichon, A., Blanc, E., Hauchecorne, A., Eds.; Springer: Dordrecht, The Netherlands, 2019; pp. 471–482. ISBN 978-3-319-75138-2. [Google Scholar] [CrossRef]
- Brachet, N.; Brown, D.; Le Bras, R.; Cansi, Y.; Mialle, P.; Coyne, J. Monitoring the Earth’s Atmosphere with the Global IMS Infrasound Network. In Infrasound Monitoring for Atmospheric Studies; Le Pichon, A., Blanc, E., Hauchecorne, A., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 77–118. ISBN 978-1-4020-9508-5. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 66–70. ISBN 978-1-4612-4380-9. [Google Scholar] [CrossRef]
- Melton, B.S.; Bailey, L.F. Multiple signal correlators. Geophysics 1957, 22, 565–588. [Google Scholar] [CrossRef]
- Olson, J.V. Infrasound signal detection using the Fisher F-statistics. Inframatics 2004, 6, 1–8. [Google Scholar]
- Cecil, D.J. LIS/OTD Gridded Lightning Climatology Data Collection; Version 2.3.2015 [0.5 Degree High Resolution Monthly Climatology (HRMC)], Data Set; NASA EOSDIS Global Hydrology Resource Center Distributed Active Archive Center: Huntsville, AL, USA, 2015. [Google Scholar] [CrossRef]
- Ern, M.; Preusse, P.; Gille, J.C.; Hepplewhite, C.L.; Mlynczak, M.G.; Russell, J.M.; Riese, M. Implications for atmospheric dynamics derived from global observations of gravity wave momentum flux in stratosphere and mesosphere. J. Geophys. Res. Atmos. 2011, 116, D19107. [Google Scholar] [CrossRef]
- Cecil, D.J.; Buechler, D.E.; Blakeslee, R.J. Gridded lightning climatology from TRMM-LIS and OTD: Dataset description. Atmos. Res. 2014, 135–136, 404–414. [Google Scholar] [CrossRef]
- Worthington, R.M.; Thomas, L. The frequency spectrum of mountain waves. Q. J. R. Meteorol. Soc. 1998, 124, 687–703. [Google Scholar] [CrossRef]
- De la Torre, A.; Alexander, P.; Hierro, R.; Llamedo, P.; Rolla, A.; Schmidt, T.; Wickert, J. Large-amplitude gravity waves above the southern Andes, the Drake Passage, and the Antarctic Peninsula. J. Geophys. Res. 2012, 117, D02106. [Google Scholar] [CrossRef]
- Hoffmann, L.; Grimsdell, A.W.; Alexander, M.J. Stratospheric gravity waves at Southern Hemisphere orographic hotspots: 2003–2014 AIRS/Aqua observations. Atmos. Chem. Phys. 2016, 16, 9381–9397. [Google Scholar] [CrossRef]
- Alexander, P.; Luna, D.; Llamedo, P.; de la Torre, A. A gravity waves study close to the Andes mountains in Patagonia and Antarctica with GPS radio occultation observations. Ann. Geophys. 2010, 28, 587–595. [Google Scholar] [CrossRef]
- Dörnbrack, A.; Gerz, T.; Schumann, U. Turbulent breaking of overturning gravity waves below a critical level. Appl. Sci. Res. 1995, 54, 163–176. [Google Scholar] [CrossRef]
- Nappo, C.J. An Introduction to Atmospheric Gravity Waves, Vol. 102 of International Geophysics; Academic Press: San Diego, CA, USA, 2012; ISBN 978-0-12-385223-6. [Google Scholar] [CrossRef]
- Sato, K.; Tateno, S.; Watanabe, S.; Kawatani, Y. Gravity wave characteristics in the Southern Hemisphere revealed by a high-resolution middle-atmospheric general circulation model. J. Atmos. Sci. 2012, 69, 1378–1396. [Google Scholar] [CrossRef]
- Jiang, Q.; Doyle, J.; Reinecke, A. A modeling study of stratospheric waves over the southern Andes and Drake Passage. J. Atmos. Sci. 2013, 70, 1668–1689. [Google Scholar] [CrossRef]
- Hauf, T.; Finke, U.; Neisser, J.; Bull, G.; Stangenberg, J.G. A Ground-Based Network for Atmospheric Pressure Fluctuations. J. Atmos. Oceanic Technol. 1996, 13, 1001–1023. [Google Scholar] [CrossRef] [Green Version]
- Plougonven, R.; Zhang, F. Internal gravity waves from atmospheric jets and fronts. Rev. Geophys. 2014, 52, 33–76. [Google Scholar] [CrossRef]
- Landès, M.; Ceranna, L.; Le Pichon, A.; Matoza, R.S. Localization of microbarom sources using the IMS infrasound network. J. Geophys. Res. 2012, 117, D06102. [Google Scholar] [CrossRef]
- Hupe, P. Global Infrasound Observations and Their Relation to Atmospheric Tides and Mountain Waves. Ph.D. Thesis, Ludwig-Maximilians-Universität, Munich, Germany, 19 December 2018. [Google Scholar]
- Hedlin, M.A.H.; Walker, K.T. A study of infrasonic anisotropy and multipathing in the atmosphere using seismic networks. Philos. Trans. Roy. Soc. Lond. A Math. Phys. Eng. Sci. 2012, 371, 1984. [Google Scholar] [CrossRef] [PubMed]
- Evers, L. Infrasound and Seismology in the Low Frequency Array LOFAR. KNMI. 2009. Available online: https://www.knmi.nl/kennis-en-datacentrum/achtergrond/infrasound-and-seismology-in-the-low-frequency-array-lofar (accessed on 5 June 2019).
- De Groot-Hedlin, C.D.; Hedlin, M.A.H. Detection of Infrasound Signals and Sources Using a Dense Seismic Network. In Infrasound Monitoring for Atmospheric Studies—Challenges in Middle-atmosphere Dynamics and Societal Benefits, 2nd ed.; Le Pichon, A., Blanc, E., Hauchecorne, A., Eds.; Springer: Dordrecht, The Netherlands, 2019; pp. 471–482. ISBN 978-3-319-75138-2. [Google Scholar] [CrossRef]
- Stammler, K.; Ceranna, L. Influence of WindTurbines on Seismic Records of the Gräfenberg Array. Seismolog. Res. Lett. 2016, 87, 1075–1081. [Google Scholar] [CrossRef]










© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hupe, P.; Ceranna, L.; Le Pichon, A. How Can the International Monitoring System Infrasound Network Contribute to Gravity Wave Measurements? Atmosphere 2019, 10, 399. https://doi.org/10.3390/atmos10070399
Hupe P, Ceranna L, Le Pichon A. How Can the International Monitoring System Infrasound Network Contribute to Gravity Wave Measurements? Atmosphere. 2019; 10(7):399. https://doi.org/10.3390/atmos10070399
Chicago/Turabian StyleHupe, Patrick, Lars Ceranna, and Alexis Le Pichon. 2019. "How Can the International Monitoring System Infrasound Network Contribute to Gravity Wave Measurements?" Atmosphere 10, no. 7: 399. https://doi.org/10.3390/atmos10070399
APA StyleHupe, P., Ceranna, L., & Le Pichon, A. (2019). How Can the International Monitoring System Infrasound Network Contribute to Gravity Wave Measurements? Atmosphere, 10(7), 399. https://doi.org/10.3390/atmos10070399