Sensitivity of the Intensity and Structure of Tropical Cyclones to Tropospheric Stability Conditions
Abstract
:1. Introduction
2. Numerical Model and Experimental Design
2.1. Numerical Model
2.2. Environmental Stability Diagnosed from Reanalysis Data
2.3. Experimental Design
3. Results
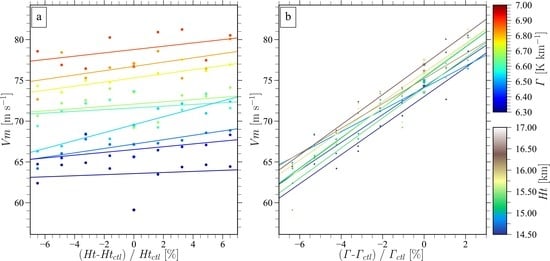
3.1. Responses of TC Intensity to Tropospheric Stability
3.2. Warm Core Structure and TC Intensity
4. Summary and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gray, W.M. Global view of the origin of tropical disturbances and storms. Mon. Wea. Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part I: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Emanuel, K.A. The maximum intensity of hurricanes. J. Atmos. Sci. 1988, 45, 1143–1155. [Google Scholar] [CrossRef]
- Rotunno, R.; Emanuel, K.A. An air–sea interaction theory for tropical cyclones. Part II: Evolutionary study using a nonhydrostatic axisymmetric numerical model. J. Atmos. Sci. 1987, 44, 542–561. [Google Scholar] [CrossRef] [Green Version]
- Holland, G.J. The maximum potential intensity of tropical cyclones. J. Atmos. Sci. 1997, 54, 2519–2541. [Google Scholar] [CrossRef]
- Bryan, G.H.; Rotunno, R. Evaluation of an analytical model for the maximum intensity of tropical cyclones. J. Atmos. Sci. 2009, 66, 3042–3060. [Google Scholar] [CrossRef] [Green Version]
- Bryan, G.H.; Rotunno, R. The maximum intensity of tropical cyclones in axisymmetric numerical model simulations. Mon. Wea. Rev. 2009, 137, 1770–1789. [Google Scholar] [CrossRef]
- Bister, M.; Emanuel, K.A. Dissipative heating and hurrican intensity. Meteor. Atmos. Phys. 1998, 65, 233–240. [Google Scholar] [CrossRef]
- Bister, M.; Emanuel, K.A. Low frequency variability of tropical cyclone potential intensity 1. Interannual to irtterdecadal variability. J. Geophys. Res. 2002, 107, 4801. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Peng, M.S.; Fu, B.; Li, T. Quantifying Environmental control on tropical cyclone intensity change. Mon. Wea. Rev. 2010, 138, 3243–3271. [Google Scholar] [CrossRef] [Green Version]
- Stovern, D.R.; Ritchie, E.A. Simulated sensitivity of tropical cyclone size and structure to the atmospheric temperature profile. J. Atmos. Sci. 2016, 73, 4553–4571. [Google Scholar] [CrossRef] [Green Version]
- Ramsay, H.A. The effects of imposed stratospheric cooling on the maximum intensity of tropical cyclones in axisymmetric radiative-convective equilibrium. J. Clim. 2013, 26, 9977–9985. [Google Scholar] [CrossRef]
- Wang, S.; Camargo, S.J.; Sobel, A.H.; Polvani, L.M. Impact of tropopause temperature on the intensity of tropical cyclones: An idealized study using a mesoscale model. J. Atmos. Sci. 2014, 71, 4333–4348. [Google Scholar] [CrossRef]
- Moon, Z.; Kieu, C. Impacts of the lower stratosphere on the development of intense tropical cyclones. Atmosphere 2017, 8, 128. [Google Scholar] [CrossRef] [Green Version]
- Shen, W.; Tuleya, R.E.; Ginis, I. A sensitivity study of the thermodynamic environment on GFDL model hurricane intensity: Implications for global warming. J. Clim. 2000, 13, 109–121. [Google Scholar] [CrossRef] [Green Version]
- Tuleya, R.E.; Bender, M.; Knutson, T.R.; Sirutis, J.J.; Thomas, B.; Ginis, I. Impact of upper-tropospheric temperature anomalies and vertical wind shear on tropical cyclone evolution using an idealized version of the operational GFDL hurricane model. J. Atmos. Sci. 2016, 73, 3803–3820. [Google Scholar] [CrossRef]
- Hill, K.A.; Lackmann, G.M. The impact of future climate change on TC intensity and structure: A downscaling approach. J. Clim. 2011, 24, 4644–4661. [Google Scholar] [CrossRef]
- Kanada, S.; Takemi, T.; Kato, M.; Yamasaki, S.; Fudeyasu, H.; Tsuboki, K.; Arakawa, O.; Takayabu, I. A multimodel intercomparison of an intense typhoon in future, warmer climates by four 5-km-mesh models. J. Clim. 2017, 30, 6017–6036. [Google Scholar] [CrossRef]
- Sato, T.; Kimura, F.; Kitoh, A. Projection of global warming onto regional precipitation over Mongolia using a regional climate model. J. Hydrol. 2007, 333, 144–154. [Google Scholar] [CrossRef]
- Takemi, T.; Okada, Y.; Ito, R.; Ishikawa, H.; Nakakita, E. Assessing the impacts of global warming on meteorological hazards and risks in Japan: Philosophy and achievements of the SOUSEI program. Hydrol. Res. Lett. 2016, 10, 119–125. [Google Scholar] [CrossRef] [Green Version]
- Takemi, T. A sensitivity of squall line intensity to environmental static stability under various shear and moisture conditions. Atmos. Res. 2007, 84, 374–389. [Google Scholar] [CrossRef]
- Takemi, T. Environmental stability control of the intensity of squall lines under low-level shear conditions. J. Geophys. Res. 2007, 112, D24110. [Google Scholar] [CrossRef] [Green Version]
- Takemi, T. Dependence of the precipitation intensity in mesoscale convective systems to temperature lapse rate. Atmos. Res. 2010, 96, 273–285. [Google Scholar] [CrossRef] [Green Version]
- Takemi, T. Convection and precipitation under various stability and shear conditions: Squall lines in tropical versus midlatitude environment. Atmos. Res. 2014, 142, 111–123. [Google Scholar] [CrossRef] [Green Version]
- Lucas, C.; Zipser, E.J.; LeMone, M.A. Vertical velocity in oceanic convection off tropical Australia. J. Atmos. Sci. 1994, 51, 3183–3193. [Google Scholar] [CrossRef]
- Bryan, G.H.; Fritsch, J.M. A benchmark simulation for moist nonhydrostatic numerical models. Mon. Wea. Rev. 2002, 130, 2917–2928. [Google Scholar] [CrossRef]
- Bryan, G.H. Effects of surface exchange coefficients and turbulence length scales on the intensity and structure of numerically simulated hurricanes. Mon. Wea. Rev. 2012, 140, 1125–1143. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteor. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- World Meteorological Organization. Definition of the tropopause. WMO Bull. 1957, 6, 136. [Google Scholar]
- Bryan, G.H.; Morrison, H. Sensitivity of a simulated squall line to horizontal resolution and parameterization of microphysics. Mon. Wea. Rev. 2012, 140, 202–225. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Takemi, T. A transition mechanism for the spontaneous axisymmetric intensification of tropical cyclones. J. Atmos. Sci. 2013, 70, 112–129. [Google Scholar] [CrossRef]
- Takemi, T.; Ito, R.; Arakawa, O. Robustness and uncertainty of projected changes in the impacts of Typhoon Vera (1959) under global warming. Hydrol. Res. Lett. 2016, 10, 88–94. [Google Scholar] [CrossRef] [Green Version]










| Parameters | Observations | ||
|---|---|---|---|
| 1% | Median | 99% | |
| Γ [K km−1] | 6.22 | 6.64 | 6.93 |
| Ht [m] | 15,230 | 16,591 | 16,723 |
| To [K] | 187.3 | 193.2 | 204.2 |
| CAPE [J kg−1] | 638 | 2927 | 4816 |
| SST [K] | 299.3 | 302.1 | 303.4 |
| Parameters | CTL | Sensitivity Experiment | PGW Mean | |
|---|---|---|---|---|
| Min. | Max. | |||
| Γ [K km−1] | 6.75 | 6.25 | 6.92 | 6.34 |
| Ht [m] | 15,375 | 14,375 | 16,375 | 16,875 |
| To [K] | 197.7 | 188.3 | 210.9 | 197.0 |
| CAPE [J kg−1] | 3091 | 1611 | 3769 | 4063 |
| SST [K] | 303.5 | 306.4 | ||
| Exp | Vm (m s−1) | Pmin (hPa) | RMW (km) | |||
|---|---|---|---|---|---|---|
| Mean | Std | Mean | std | Mean | std | |
| CTL | 73.55 | 2.0 | 886.4 | 4.5 | 23.93 | 2.32 |
| Htctl—To+6K | 59.11 | 4.6 | 925.1 | 9.2 | 20.89 | 1.17 |
| Htctl—To−2K | 76.70 | 2.8 | 875.8 | 6.7 | 25.88 | 2.89 |
| Ht−1km—Toctl | 74.32 | 2.4 | 883.2 | 5.7 | 24.42 | 1.74 |
| Ht+1km—Toctl | 76.94 | 2.0 | 875.4 | 5.7 | 22.86 | 2.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takemi, T.; Yamasaki, S. Sensitivity of the Intensity and Structure of Tropical Cyclones to Tropospheric Stability Conditions. Atmosphere 2020, 11, 411. https://doi.org/10.3390/atmos11040411
Takemi T, Yamasaki S. Sensitivity of the Intensity and Structure of Tropical Cyclones to Tropospheric Stability Conditions. Atmosphere. 2020; 11(4):411. https://doi.org/10.3390/atmos11040411
Chicago/Turabian StyleTakemi, Tetsuya, and Shota Yamasaki. 2020. "Sensitivity of the Intensity and Structure of Tropical Cyclones to Tropospheric Stability Conditions" Atmosphere 11, no. 4: 411. https://doi.org/10.3390/atmos11040411
APA StyleTakemi, T., & Yamasaki, S. (2020). Sensitivity of the Intensity and Structure of Tropical Cyclones to Tropospheric Stability Conditions. Atmosphere, 11(4), 411. https://doi.org/10.3390/atmos11040411