Investigating Whether the Ensemble Average of Multi-Global-Climate-Models Can Necessarily Better Project Seasonal Drought Conditions in China
Abstract
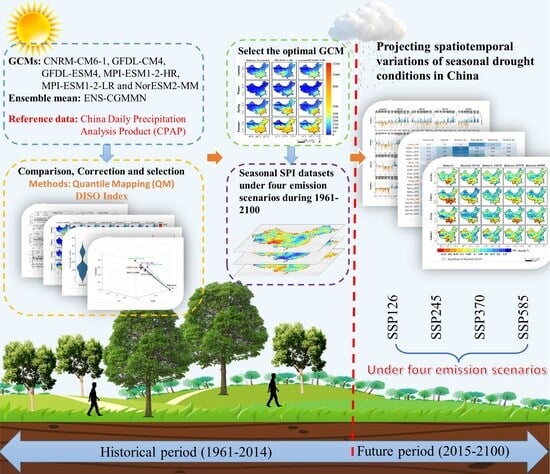
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Utilized and Processing
2.2.1. Reference Precipitation Observations
2.2.2. Global Climate Model (GCM)
2.3. Methods
2.3.1. Quantile Mapping (QM) Method
2.3.2. DISO Index
2.3.3. Standardized Precipitation Index (SPI)
3. Results
3.1. Inter-Comparisons between GCMs and Reference Precipitation
3.2. Evaluation and Correction of GCMs and ENS-CGMMN
3.3. Spatiotemporal Variations of Seasonal Drought Conditions in China
4. Discussion
4.1. Uncertainty in the Standardized Precipitation Index
4.2. Reasonality of the Main Findings in this Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Full Name |
|---|---|
| XJ | Xinjiang |
| QTP | Qinghai–Tibetan Plateau |
| NW | Northwest |
| NE | Northeast |
| NC | Northern China |
| SW | Southwest |
| SC | Southern China |
| QM | quantile mapping |
| SPI | standardized precipitation index |
| CPAP | China Daily Precipitation Analysis Product |
| GCM | global climate models |
| RCP | Representative Concentration Pathway |
| SSP | Shared Socioeconomic Pathway |
| CMIP | Coupled Model Intercomparison Project |
| IPCC | Intergovernmental Panel on Climate Change |
| AR | Assessment Report |
| CMA | China Meteorological Administration |
| CC | correlation coefficient |
| RMSE | root-mean square error |
| SD | standard deviation |
| AE | absolute error |
References
- Otkin, J.A.; Svoboda, M.; Hunt, E.D.; Ford, T.W.; Anderson, M.C.; Hain, C.; Basara, J.B. Flash Droughts: A Review and Assessment of the Challenges Imposed by Rapid-Onset Droughts in the United States. Bull. Am. Meteorol. Soc. 2018, 99, 911–919. [Google Scholar] [CrossRef]
- Jia, H.; Chen, F.; Zhang, C.; Dong, J.; Du, E.; Wang, L. High emissions could increase the future risk of maize drought in China by 60–70%. Sci. Total Environ. 2022, 852, 158474. [Google Scholar] [CrossRef] [PubMed]
- FAO. The Impact of Natural Hazards and Disasters on Agriculture and Food Security and Nutrition: A Call for Action to Build Resilient Livelihoods; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015. [Google Scholar]
- Su, B.; Huang, J.; Fischer, T.; Wang, Y.; Kundzewicz, Z.W.; Zhai, J.; Sun, H.; Wang, A.; Zeng, X.; Wang, G.; et al. Drought losses in China might double between the 1.5 °C and 2.0 °C warming. Proc. Natl. Acad. Sci. USA 2018, 115, 10600–10605. [Google Scholar] [CrossRef]
- Yu, M.; Li, Q.; Hayes, M.J.; Svoboda, M.D.; Heim, R.R. Are droughts becoming more frequent or severe in China based on the standardized precipitation evapotranspiration index: 1951–2010? Int. J. Climatol. 2014, 34, 545–558. [Google Scholar] [CrossRef]
- Bose, A.K.; Gessler, A.; Bolte, A.; Bottero, A.; Buras, A.; Cailleret, M.; Camarero, J.J.; Haeni, M.; Hereş, A.M.; Hevia, A. Growth and resilience responses of Scots pine to extreme droughts across Europe depend on predrought growth conditions. Glob. Chang. Biol. 2020, 26, 4521–4537. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Da Rocha Júnior, R.L.; dos Santos Silva, F.D.; Costa, R.L.; Gomes, H.B.; Pinto, D.D.C.; Herdies, D.L. Bivariate Assessment of Drought Return Periods and Frequency in Brazilian Northeast Using Joint Distribution by Copula Method. Geosciences 2020, 10, 135. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- Zhang, Q.; Yao, Y.; Li, Y.; Huang, J.; Ma, Z.; Wang, Z.; Wang, S.; Wang, Y.; Zhang, Y. Progress and prospect on the study of causes and variation regularity of droughts in China. Acta Meteor. Sin. 2020, 78, 500–521. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Yang, Y.; Chen, J.; Gu, L.; Wang, J.; He, S.; Wu, B.; Xiong, J. Projection of droughts and their socioeconomic exposures based on terrestrial water storage anomaly over China. Sci. China Earth Sci. 2022, 65, 1772–1787. [Google Scholar] [CrossRef]
- Kogan, F.N. Global drought watch from space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Liu, Y.; You, M.; Zhu, J.; Wang, F.; Ran, R. Integrated risk assessment for agricultural drought and flood disasters based on entropy information diffusion theory in the middle and lower reaches of the Yangtze River, China. Int. J. Disaster Risk Reduct. 2019, 38, 101194. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, J.; Tong, Z.; Han, A.; Zhi, F. Ecological security assessment of Xilingol grassland in China using DPSIRM model. Ecol. Indic. 2022, 143, 109336. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, J.; Shalamzari, M.J.; Arshad, A.; Liu, S.; Liu, T.; Tao, H. Monitoring Recent Changes in Drought and Wetness in the Source Region of the Yellow River Basin, China. Water 2022, 14, 861. [Google Scholar] [CrossRef]
- Grigorieva, E.A.; Livenets, A.S. Risks to the Health of Russian Population from Floods and Droughts in 2010–2020: A Scoping Review. Climate 2022, 10, 37. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Odongo, R.A.; De Moel, H.; Van Loon, A.F. Propagation from meteorological to hydrological drought in the Horn of Africa using both standardized and threshold-based indices. Nat. Hazards Earth Syst. Sci. 2023, 23, 2365–2386. [Google Scholar] [CrossRef]
- Sepulcre-Canto, G.; Horion, S.; Singleton, A.; Carrao, H.; Vogt, J. Development of a Combined Drought Indicator to detect agricultural drought in Europe. Nat. Hazards Earth Syst. Sci. 2012, 12, 3519–3531. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Weiss, A.; Hu, Q. An evaluation of the Standardized Precipitation Index, the China-Z Index and the statistical Z-Score. Int. J. Climatol. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- Ju, X.; Yang, X.; Chen, L.; Wang, Y. Research on determination of station indexes and division of regional flood/drought grades in China. J. Appl. Meteorol. 1997, 8, 26–33. [Google Scholar]
- Byun, H.-R.; Wilhite, D.A. Daily quantification of drought severity and duration. J. Clim. 1996, 5, 1181–1201. [Google Scholar]
- Hao, Z.; AghaKouchak, A. A Nonparametric Multivariate Multi-Index Drought Monitoring Framework. J. Hydrometeorol. 2014, 15, 89–101. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate standardized drought index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Blain, G.C.; da Rocha Sobierajski, G.; Weight, E.; Martins, L.L.; Xavier, A.C.F. Improving the interpretation of standardized precipitation index estimates to capture drought characteristics in changing climate conditions. Int. J. Climatol. 2022, 42, 5586–5608. [Google Scholar] [CrossRef]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal drought analysis by the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Fung, K.; Huang, Y.; Koo, C. Assessing drought conditions through temporal pattern, spatial characteristic and operational accuracy indicated by SPI and SPEI: Case analysis for Peninsular Malaysia. Nat. Hazards 2020, 103, 2071–2101. [Google Scholar] [CrossRef]
- Adisa, O.M.; Masinde, M.; Botai, J.O. Assessment of the dissimilarities of EDI and SPI measures for drought determination in South Africa. Water 2021, 13, 82. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Pande, C.B.; Kumar, M.; Tolche, A.D.; Singh, S.K.; Kumar, A.; Vishwakarma, D.K. Prediction of meteorological drought and standardized precipitation index based on the random forest (RF), random tree (RT), and Gaussian process regression (GPR) models. Environ. Sci. Pollut. Res. 2023, 30, 43183–43202. [Google Scholar] [CrossRef] [PubMed]
- Zuo, D.-D.; Hou, W.; Zhang, Q.; Yan, P.-C. Sensitivity analysis of standardized precipitation index to climate state selection in China. Adv. Clim. Chang. Res. 2022, 13, 42–50. [Google Scholar] [CrossRef]
- Ridder, N.N.; Pitman, A.J.; Ukkola, A.M. Do CMIP6 climate models simulate global or regional compound events skillfully? Geophys. Res. Lett. 2021, 48, e2020GL091152. [Google Scholar] [CrossRef]
- Grose, M.R.; Narsey, S.; Delage, F.P.; Dowdy, A.J.; Bador, M.; Boschat, G.; Chung, C.; Kajtar, J.B.; Rauniyar, S.; Freund, M.B.; et al. Insights From CMIP6 for Australia′s Future Climate. Earth′s Future 2020, 8, e2019EF001469. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N.; Saeed, F.; Saeed, S.; Ismail, M.; Ehsan, M.A.; Diallo, I.; O’Brien, E.; Ashfaq, M.; Martínez-Castro, D.; et al. Projected Changes in Temperature and Precipitation Over the United States, Central America, and the Caribbean in CMIP6 GCMs. Earth Syst. Environ. 2021, 5, 1–24. [Google Scholar] [CrossRef]
- Meinshausen, M.; Nicholls, Z.R.; Lewis, J.; Gidden, M.J.; Vogel, E.; Freund, M.; Beyerle, U.; Gessner, C.; Nauels, A.; Bauer, N. The shared socio-economic pathway (SSP) greenhouse gas concentrations and their extensions to 2500. Geosci. Model Dev. 2020, 13, 3571–3605. [Google Scholar] [CrossRef]
- Qing, Y.; Wang, S.; Zhang, B.; Wang, Y. Ultra-high resolution regional climate projections for assessing changes in hydrological extremes and underlying uncertainties. Clim. Dyn. 2020, 55, 2031–2051. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, J.; Li, W.; Sun, C.; Li, L. Does CMIP6 Inspire More Confidence in Simulating Climate Extremes over China? Adv. Atmos. Sci. 2020, 37, 1119–1132. [Google Scholar] [CrossRef]
- Xin, X.; Wu, T.; Zhang, J.; Yao, J.; Fang, Y. Comparison of CMIP6 and CMIP5 simulations of precipitation in China and the East Asian summer monsoon. Int. J. Climatol. 2020, 40, 6423–6440. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Mondal, S.K.; Zhai, J.; Wang, Y.; Wen, S.; Gao, M.; Lv, Y.; Jiang, S.; Jiang, T.; et al. Insight from CMIP6 SSP-RCP scenarios for future drought characteristics in China. Atmos. Res. 2021, 250, 105375. [Google Scholar] [CrossRef]
- Sabeerali, C.; Rao, S.A.; Dhakate, A.; Salunke, K.; Goswami, B. Why ensemble mean projection of south Asian monsoon rainfall by CMIP5 models is not reliable? Clim. Dyn. 2015, 45, 161–174. [Google Scholar] [CrossRef]
- Aadhar, S.; Mishra, V. On the Projected Decline in Droughts Over South Asia in CMIP6 Multimodel Ensemble. J. Geophys. Res. Atmos. 2020, 125, e2020JD033587. [Google Scholar] [CrossRef]
- Yazdandoost, F.; Moradian, S.; Izadi, A.; Aghakouchak, A. Evaluation of CMIP6 precipitation simulations across different climatic zones: Uncertainty and model intercomparison. Atmos. Res. 2021, 250, 105369. [Google Scholar] [CrossRef]
- Abdulai, P.J.; Chung, E.-S. Uncertainty Assessment in Drought Severities for the Cheongmicheon Watershed Using Multiple GCMs and the Reliability Ensemble Averaging Method. Sustainability 2019, 11, 4283. [Google Scholar] [CrossRef]
- Alamgir, M.; Khan, N.; Shahid, S.; Yaseen, Z.M.; Dewan, A.; Hassan, Q.; Rasheed, B. Evaluating severity–area–frequency (SAF) of seasonal droughts in Bangladesh under climate change scenarios. Stoch. Environ. Res. Risk Assess. 2020, 34, 447–464. [Google Scholar] [CrossRef]
- Ueda, H.; Iwai, A.; Kuwako, K.; Hori, M.E. Impact of anthropogenic forcing on the Asian summer monsoon as simulated by eight GCMs. Geophys. Res. Lett. 2006, 33, L06703. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Sivakumar, M.V.; Pulwarty, R. Managing drought risk in a changing climate: The role of national drought policy. Weather. Clim. Extrem. 2014, 3, 4–13. [Google Scholar] [CrossRef]
- Zou, X.; Zhai, P.; Zhang, Q. Variations in droughts over China: 1951–2003. Geophys. Res. Lett. 2005, 32, L04707. [Google Scholar] [CrossRef]
- Nam, W.-H.; Hayes, M.J.; Svoboda, M.D.; Tadesse, T.; Wilhite, D.A. Drought hazard assessment in the context of climate change for South Korea. Agric. Water Manag. 2015, 160, 106–117. [Google Scholar] [CrossRef]
- Haro, D.; Solera, A.; Paredes, J.; Andreu, J. Methodology for drought risk assessment in within-year regulated reservoir systems. Application to the Orbigo River system (Spain). Water Resour. Manag. 2014, 28, 3801–3814. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Lai, C.; Zeng, Z.; Zhong, R.; Chen, X.; Zhou, X.; Wang, M. Does drought in China show a significant decreasing trend from 1961 to 2009? Sci. Total Environ. 2017, 579, 314–324. [Google Scholar] [CrossRef]
- Zhai, Y.; Guo, Y.; Zhou, J.; Guo, N.; Wang, J.; Teng, Y. The spatio-temporal variability of annual precipitation and its local impact factors during 1724–2010 in Beijing, China. Hydrol. Process. 2014, 28, 2192–2201. [Google Scholar] [CrossRef]
- Qian, W.; Kang, H.-S.; Lee, D.-K. Distribution of seasonal rainfall in the East Asian monsoon region. Theor. Appl. Climatol. 2002, 73, 151–168. [Google Scholar] [CrossRef]
- Wu, Z.-Y.; Lu, G.-H.; Wen, L.; Lin, C. Reconstructing and analyzing China’s fifty-nine year (1951–2009) drought history using hydrological model simulation. Hydrol. Earth Syst. Sci. 2011, 15, 2881–2894. [Google Scholar] [CrossRef]
- Lei, Y.; Hoskins, B.; Slingo, J. Exploring the Interplay between Natural Decadal Variability and Anthropogenic Climate Change in Summer Rainfall over China. Part I: Observational Evidence. J. Clim. 2011, 24, 4584–4599. [Google Scholar] [CrossRef]
- Zhou, L.-T. Impact of East Asian winter monsoon on rainfall over southeastern China and its dynamical process. Int. J. Climatol. 2011, 31, 677–686. [Google Scholar] [CrossRef]
- Liu, J.; Ren, Y.; Tao, H.; Shalamzari, M.J. Spatial and Temporal Variation Characteristics of Heatwaves in Recent Decades over China. Remote Sens. 2021, 13, 3824. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, Y.; Shen, Y.; Zhang, S. Evaluation of Global Satellite Mapping of Precipitation Project Daily Precipitation Estimates over the Chinese Mainland. Adv. Meteorol. 2016, 2016, 9365294. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Liu, T.; Li, Q. Runoff Dynamics and Associated Multi-Scale Responses to Climate Changes in the Middle Reach of the Yarlung Zangbo River Basin, China. Water 2018, 10, 295. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W. Climate Changes and Associated Multiscale Impacts on Watershed Discharge over the Upper Reach of Yarlung Zangbo River Basin, China. Adv. Meteorol. 2018, 2018, 4851645. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the Triple Collocation method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Zhong, R.; Chen, X.; Lai, C.; Wang, Z.; Lian, Y.; Yu, H.; Wu, X. Drought monitoring utility of satellite-based precipitation products across mainland China. J. Hydrol. 2019, 568, 343–359. [Google Scholar] [CrossRef]
- Wei, L.; Jiang, S.; Ren, L.; Wang, M.; Zhang, L.; Liu, Y.; Yuan, F.; Yang, X. Evaluation of seventeen satellite-, reanalysis-, and gauge-based precipitation products for drought monitoring across mainland China. Atmos. Res. 2021, 263, 105813. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, L. Projection of climate extremes in China, an incremental exercise from CMIP5 to CMIP6. Sci. Bull. 2021, 66, 2528–2537. [Google Scholar] [CrossRef] [PubMed]
- Change, N.C. The CMIP6 landscape. Clim. Chang. 2019, 9, 727. [Google Scholar]
- Li, S.-Y.; Miao, L.-J.; Jiang, Z.-H.; Wang, G.-J.; Gnyawali, K.R.; Zhang, J.; Zhang, H.; Fang, K.; He, Y.; Li, C. Projected drought conditions in Northwest China with CMIP6 models under combined SSPs and RCPs for 2015–2099. Adv. Clim. Chang. Res. 2020, 11, 210–217. [Google Scholar] [CrossRef]
- O′Neill, B.C.; Tebaldi, C.; Van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J. The scenario model intercomparison project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Dey, A.; Sahoo, D.P.; Kumar, R.; Remesan, R. A multimodel ensemble machine learning approach for CMIP6 climate model projections in an Indian River basin. Int. J. Climatol. 2022, 42, 9215–9236. [Google Scholar] [CrossRef]
- Baghanian, S.; Alizadeh, M.J. Wave climate projection in the Persian Gulf: An ensemble of statistically downscaled CMIP6-GCMs. Ocean. Eng. 2022, 266, 112821. [Google Scholar] [CrossRef]
- Accadia, C.; Mariani, S.; Casaioli, M.; Lavagnini, A.; Speranza, A. Sensitivity of Precipitation Forecast Skill Scores to Bilinear Interpolation and a Simple Nearest-Neighbor Average Method on High-Resolution Verification Grids. Weather. Forecast. 2003, 18, 918–932. [Google Scholar] [CrossRef]
- Jitariu, V.; Ichim, P.; Sfica, L.; Ursu, A. Climate Change Projections Regarding Apple Orchards in the North-Eastern Region of Romania. Int. Multidiscip. Sci. GeoConf. SGEM 2019, 19, 915–923. [Google Scholar]
- Morsy, M.; Moursy, F.I.; Sayad, T.; Shaban, S. Climatological study of SPEI drought index using observed and CRU gridded dataset over Ethiopia. Pure Appl. Geophys. 2022, 179, 3055–3073. [Google Scholar] [CrossRef]
- Burdanowitz, J.; Klepp, C.; Bakan, S.; Buehler, S.A. Simulation of ship-track versus satellite-sensor differences in oceanic precipitation using an island-based radar. Remote Sens. 2017, 9, 593. [Google Scholar] [CrossRef]
- Janjic, J.; Gallagher, S.; Gleeson, E.; Dias, F. Wave energy potential in the northeast Atlantic: Impact of large-scale atmospheric oscillations. In Proceedings of the 1st Workshop on Waves, Storm Surges and Coastal Hazards, Liverpool, UK, 11–15 September 2017; pp. 1–5. [Google Scholar]
- Enayati, M.; Bozorg-Haddad, O.; Bazrafshan, J.; Hejabi, S.; Chu, X. Bias correction capabilities of quantile mapping methods for rainfall and temperature variables. J. Water Clim. Chang. 2020, 12, 401–419. [Google Scholar] [CrossRef]
- Reiter, P.; Gutjahr, O.; Schefczyk, L.; Heinemann, G.; Casper, M. Does applying quantile mapping to subsamples improve the bias correction of daily precipitation? Int. J. Climatol. 2018, 38, 1623–1633. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.; Haugen, J.; Skaugen, T.E. Downscaling RCM precipitation to the station scale using quantile mapping–a comparison of methods. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 6185–6201. [Google Scholar]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.; Best, M.; Gomes, S.; Viterbo, P.; Hagemann, S.; Haerter, J. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Ines, A.V.; Hansen, J.W. Bias correction of daily GCM rainfall for crop simulation studies. Agric. For. Meteorol. 2006, 138, 44–53. [Google Scholar] [CrossRef]
- Osuch, M.; Lawrence, D.; Meresa, H.K.; Napiorkowski, J.J.; Romanowicz, R.J. Projected changes in flood indices in selected catchments in Poland in the 21st century. Stoch. Environ. Res. Risk Assess. 2017, 31, 2435–2457. [Google Scholar] [CrossRef]
- Villani, V.; Rianna, G.; Mercogliano, P.; Zollo, A.L. Statistical approaches versus weather generator to downscale RCM outputs to slope scale for stability assessment: A comparison of performances. Electron. J. Geotech. Eng. 2015, 20, 1495–1515. [Google Scholar]
- Kouhestani, S.; Eslamian, S.S.; Abedi-Koupai, J.; Besalatpour, A.A. Projection of climate change impacts on precipitation using soft-computing techniques: A case study in Zayandeh-rud Basin, Iran. Glob. Planet. Chang. 2016, 144, 158–170. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Kalmár, T.; Pieczka, I.; Pongrácz, R. A sensitivity analysis of the different setups of the RegCM4.5 model for the Carpathian region. Int. J. Climatol. 2021, 41, E1180–E1201. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, D.; Chen, X.; Zhou, Q.; Peng, Y.; Li, J.; Sang, Y. CCHZ-DISO: A Timely New Assessment System for Data Quality or Model Performance From Da Dao Zhi Jian. Geophys. Res. Lett. 2022, 49, e2022GL100681. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, X.; Zhou, Q.; Chen, D.; Li, J. DISO: A rethink of Taylor diagram. Int. J. Climatol. 2019, 39, 2825–2832. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, D.; Hu, Z.; Chen, X. Decompositions of Taylor diagram and DISO performance criteria. Int. J. Climatol. 2021, 41, 5726–5732. [Google Scholar] [CrossRef]
- Naresh Kumar, M.; Murthy, C.S.; Sesha Sai, M.V.R.; Roy, P.S. On the use of Standardized Precipitation Index (SPI) for drought intensity assessment. Meteorol. Appl. 2009, 16, 381–389. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, R.; Qi, J.; Zeng, J.; Wu, J.; Shui, W.; Wu, X.; Li, J. An improved daily standardized precipitation index dataset for mainland China from 1961 to 2018. Sci. Data 2022, 9, 124. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Standard precipitation index drought forecasting using neural networks, wavelet neural networks, and support vector regression. Appl. Comput. Intell. Soft Comput. 2012, 2012, 794061. [Google Scholar] [CrossRef]
- Kumar, R.; Musuuza, J.L.; Van Loon, A.F.; Teuling, A.J.; Barthel, R.; Ten Broek, J.; Mai, J.; Samaniego, L.; Attinger, S. Multiscale evaluation of the Standardized Precipitation Index as a groundwater drought indicator. Hydrol. Earth Syst. Sci. 2016, 20, 1117–1131. [Google Scholar] [CrossRef]
- Farahmand, A.; AghaKouchak, A. A generalized framework for deriving nonparametric standardized drought indicators. Adv. Water Resour. 2015, 76, 140–145. [Google Scholar] [CrossRef]
- Moradian, S.; Yazdandoost, F. Seasonal meteorological drought projections over Iran using the NMME data. Nat. Hazards 2021, 108, 1089–1107. [Google Scholar] [CrossRef]
- Gringorten, I.I. A plotting rule for extreme probability paper. J. Geophys. Res. 1963, 68, 813–814. [Google Scholar] [CrossRef]
- Pramudya, Y.; Onishi, T. Assessment of the Standardized Precipitation Index (SPI) in Tegal City, Central Java, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2018, 129, 012019. [Google Scholar] [CrossRef]
- Hänsel, S. Changes in the Characteristics of Dry and Wet Periods in Europe (1851–2015). Atmosphere 2020, 11, 1080. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Yang, H.; Li, Z.; Qin, Y.; Shen, Y. Spatio-temporal variation of drought in China during 1961–2012: A climatic perspective. J. Hydrol. 2015, 526, 253–264. [Google Scholar] [CrossRef]
- Shah, R.; Bharadiya, N.; Manekar, V. Drought Index Computation Using Standardized Precipitation Index (SPI) Method For Surat District, Gujarat. Aquat. Procedia 2015, 4, 1243–1249. [Google Scholar] [CrossRef]
- Maurer, E.P.; Pierce, D.W. Bias correction can modify climate model simulated precipitation changes without adverse effect on the ensemble mean. Hydrol. Earth Syst. Sci. 2014, 18, 915–925. [Google Scholar] [CrossRef]
- Singh, V.; Jain, S.K.; Singh, P.K. Inter-comparisons and applicability of CMIP5 GCMs, RCMs and statistically downscaled NEX-GDDP based precipitation in India. Sci. Total Environ. 2019, 697, 134163. [Google Scholar] [CrossRef]
- Kwon, S.-H.; Kim, J.; Boo, K.-O.; Shim, S.; Kim, Y.; Byun, Y.-H. Performance-based projection of the climate-change effects on precipitation extremes in East Asia using two metrics. Int. J. Climatol. 2019, 39, 2324–2335. [Google Scholar] [CrossRef]
- Liu, J.; Shangguan, D.; Liu, S.; Ding, Y.; Wang, S.; Wang, X. Evaluation and comparison of CHIRPS and MSWEP daily-precipitation products in the Qinghai-Tibet Plateau during the period of 1981–2015. Atmos. Res. 2019, 230, 104634. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, T.; Frauenfeld, O.W.; Ye, B.; Yang, D.; Qin, D. Evaluation of precipitation from the ERA-40, NCEP-1, and NCEP-2 Reanalyses and CMAP-1, CMAP-2, and GPCP-2 with ground-based measurements in China. J. Geophys. Res. Atmos. 2009, 114, D09105. [Google Scholar] [CrossRef]
- Vergni, L.; Di Lena, B.; Todisco, F.; Mannocchi, F. Uncertainty in drought monitoring by the Standardized Precipitation Index: The case study of the Abruzzo region (central Italy). Theor. Appl. Climatol. 2017, 128, 13–26. [Google Scholar] [CrossRef]
- Karamuz, E.; Bogdanowicz, E.; Senbeta, T.B.; Napiórkowski, J.J.; Romanowicz, R.J. Is It a Drought or Only a Fluctuation in Precipitation Patterns?—Drought Reconnaissance in Poland. Water 2021, 13, 807. [Google Scholar] [CrossRef]
- Pei, W.; Tian, C.; Fu, Q.; Ren, Y.; Li, T. Risk analysis and influencing factors of drought and flood disasters in China. Nat. Hazards 2022, 110, 1599–1620. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Lu, J.; Jia, L.; Menenti, M.; Yan, Y.; Zheng, C.; Zhou, J. Performance of the Standardized Precipitation Index Based on the TMPA and CMORPH Precipitation Products for Drought Monitoring in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1387–1396. [Google Scholar] [CrossRef]
- Dong, J.; Akbar, R.; Short Gianotti, D.J.; Feldman, A.F.; Crow, W.T.; Entekhabi, D. Can Surface Soil Moisture Information Identify Evapotranspiration Regime Transitions? Geophys. Res. Lett. 2022, 49, e2021GL097697. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, H.; Chen, J.; Fu, G.; Zhan, C.; Yang, H. Quantitative analysis of nonlinear climate change impact on drought based on the standardized precipitation and evapotranspiration index. Ecol. Indic. 2021, 121, 107107. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Su, T.; Feng, T.; Huang, B.; Han, Z.; Qian, Z.; Feng, G.; Hou, W.; Dong, W. Long-term mean changes in actual evapotranspiration over China under climate warming and the attribution analysis within the Budyko framework. Int. J. Climatol. 2022, 42, 1136–1147. [Google Scholar] [CrossRef]
- Pan, S.; Pan, N.; Tian, H.; Friedlingstein, P.; Sitch, S.; Shi, H.; Arora, V.K.; Haverd, V.; Jain, A.K.; Kato, E.; et al. Evaluation of global terrestrial evapotranspiration using state-of-the-art approaches in remote sensing, machine learning and land surface modeling. Hydrol. Earth Syst. Sci. 2020, 24, 1485–1509. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, C.; Tao, H.; Zhu, J.; Kundzewicz, Z.W. Projections of actual evapotranspiration under the 1.5 °C and 2.0 °C global warming scenarios in sandy areas in northern China. Sci. Total Environ. 2018, 645, 1496–1508. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Wang, L.; Yang, W. Comparative Analysis of Drought Indicated by the SPI and SPEI at Various Timescales in Inner Mongolia, China. Water 2020, 12, 1925. [Google Scholar] [CrossRef]
- Jia, K.; Ruan, Y.; Yang, Y.; Zhang, C. Assessing the Performance of CMIP5 Global Climate Models for Simulating Future Precipitation Change in the Tibetan Plateau. Water 2019, 11, 1771. [Google Scholar] [CrossRef]
- Jiang, D.; Hu, D.; Tian, Z.; Lang, X. Differences between CMIP6 and CMIP5 models in simulating climate over China and the East Asian monsoon. Adv. Atmos. Sci. 2020, 37, 1102–1118. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, J.; Xiong, Z.; Wang, S.; Yuan, J. An intercomparison of multiple statistical downscaling methods for daily precipitation and temperature over China: Present climate evaluations. Clim. Dyn. 2019, 53, 4629–4649. [Google Scholar] [CrossRef]
- Tong, Y.; Gao, X.; Han, Z.; Xu, Y.; Xu, Y.; Giorgi, F. Bias correction of temperature and precipitation over China for RCM simulations using the QM and QDM methods. Clim. Dyn. 2021, 57, 1425–1443. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.-S.; Shahid, S. The New Bias Correction Method for Daily Extremes Precipitation over South Korea using CMIP6 GCMs. Water Resour. Manag. 2022, 36, 5977–5997. [Google Scholar] [CrossRef]
- Gupta, V.; Singh, V.; Jain, M.K. Assessment of precipitation extremes in India during the 21st century under SSP1-1.9 mitigation scenarios of CMIP6 GCMs. J. Hydrol. 2020, 590, 125422. [Google Scholar] [CrossRef]
- Aadhar, S.; Mishra, V. A substantial rise in the area and population affected by dryness in South Asia under 1.5 C, 2.0 C and 2.5 C warmer worlds. Environ. Res. Lett. 2019, 14, 114021. [Google Scholar] [CrossRef]
- Seager, R.; Naik, N.; Vecchi, G.A. Thermodynamic and Dynamic Mechanisms for Large-Scale Changes in the Hydrological Cycle in Response to Global Warming. J. Clim. 2010, 23, 4651–4668. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, T.; Zhang, L.; Chen, X.; Zhang, W.; Jiang, J. Global Land Monsoon Precipitation Changes in CMIP6 Projections. Geophys. Res. Lett. 2020, 47, e2019GL086902. [Google Scholar] [CrossRef]
- Ashfaq, M.; Rastogi, D.; Mei, R.; Touma, D.; Ruby Leung, L. Sources of errors in the simulation of south Asian summer monsoon in the CMIP5 GCMs. Clim. Dyn. 2017, 49, 193–223. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W. A CMIP5 multimodel projection of future temperature, precipitation, and climatological drought in China. Int. J. Climatol. 2014, 34, 2059–2078. [Google Scholar] [CrossRef]
- Xu, H.; Chen, H.; Wang, H. Future changes in precipitation extremes across China based on CMIP6 models. Int. J. Climatol. 2022, 42, 635–651. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef]









| Model | Number of Ensembles | Spatial Resolution | Time Series | |||||
|---|---|---|---|---|---|---|---|---|
| Hindcast | SSP126 | SSP245 | SSP370 | SSP585 | Lat/Lon | Hindcast | Projection | |
| CNRM-CM6-1 | 30 | 6 | 6 | 6 | 6 | 1.4 × 1.4 degree | January 1961 to December 2014 | January 2015 to December 2100 |
| GFDL-ESM4 | 3 | 1 | 3 | 1 | 1 | 1.0 × 1.25 degree | ||
| MPI-ESM1-2-HR | 10 | 2 | 2 | 10 | 2 | 0.93 × 0.93 degree | ||
| MPI-ESM1-2-LR | 31 | 30 | 30 | 30 | 30 | 1.86 × 1.87 degree | ||
| NorESM2-MM | 3 | 1 | 2 | 1 | 1 | 0.9 × 1.25 degree | ||
| Models | CC | AE (mm) | RMSE (mm) | DISO 1 |
|---|---|---|---|---|
| CNRM-CM6-1 | 0.98 | 51.19 | 55.87 | 1.18 |
| GFDL-ESM4 | 0.97 | 41.55 | 48.93 | 1.00 |
| MPI-ESM1-2-HR | 0.94 | 37.07 | 52.41 | 0.98 |
| MPI-ESM1-2-LR | 0.95 | 58.71 | 69.80 | 1.42 |
| NorESM2-MM | 0.98 | 49.94 | 59.53 | 1.20 |
| ENS-CGMMN | 0.97 | 47.69 | 55.03 | 1.13 |
| Models | CC | AE (mm) | RMSE (mm) | DISO 1 |
|---|---|---|---|---|
| GFDL-ESM4 | 0.98 | 0.06 | 20.78 | 0.97 |
| MPI-ESM1-2-HR | 0.98 | 0.02 | 20.87 | 0.97 |
| ENS-CGMMN | 0.98 | −0.04 | 21.58 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Ren, Y.; Willems, P.; Liu, T.; Yong, B.; Shalamzari, M.J.; Gao, H. Investigating Whether the Ensemble Average of Multi-Global-Climate-Models Can Necessarily Better Project Seasonal Drought Conditions in China. Atmosphere 2023, 14, 1408. https://doi.org/10.3390/atmos14091408
Liu J, Ren Y, Willems P, Liu T, Yong B, Shalamzari MJ, Gao H. Investigating Whether the Ensemble Average of Multi-Global-Climate-Models Can Necessarily Better Project Seasonal Drought Conditions in China. Atmosphere. 2023; 14(9):1408. https://doi.org/10.3390/atmos14091408
Chicago/Turabian StyleLiu, Jinping, Yanqun Ren, Patrick Willems, Tie Liu, Bin Yong, Masoud Jafari Shalamzari, and Huiran Gao. 2023. "Investigating Whether the Ensemble Average of Multi-Global-Climate-Models Can Necessarily Better Project Seasonal Drought Conditions in China" Atmosphere 14, no. 9: 1408. https://doi.org/10.3390/atmos14091408
APA StyleLiu, J., Ren, Y., Willems, P., Liu, T., Yong, B., Shalamzari, M. J., & Gao, H. (2023). Investigating Whether the Ensemble Average of Multi-Global-Climate-Models Can Necessarily Better Project Seasonal Drought Conditions in China. Atmosphere, 14(9), 1408. https://doi.org/10.3390/atmos14091408