On the Possible Origin of Chaotic Pulse Trains in Lightning Flashes

Abstract

In this study, electromagnetic field radiation bursts known as chaotic pulse trains (CPTs) and regular pulse trains (RPTs) generated by lightning flashes were analyzed. Through a numerical analysis it was found that a typical CPT could be generated by superimposing several RPTs onto each other. It is suggested that the chaotic pulse trains are created by a superposition of several regular pulse trains. Since regular pulse trains are probably created by dart or dart-stepped leaders or K-changes inside the cloud, chaotic pulse trains are caused by the superposition of electric fields caused by more than one of these leaders or K-changes propagating simultaneously. The hypothesis is supported by the fact that one can find regular pulse trains either in the beginning, middle or later stages of chaotic pulse trains.

1. Introduction

Regular pulse trains (RPTs) consist of a train of pulses each with a signature similar to electric field pulses generated by dart leaders. According to Krider et al. [1], RPTs are generated by a dart-stepped leader or K-changes type discharges propagating inside the cloud. Each pulse train had a typical duration of 100–400 µs with a mean time interval between individual pulses of about 5–6 µs. The total duration of a single pulse was typically 1–2 µs with a pulse width at full width at half maximum (FWHM) of about 0.75 µs. According to Rakov et al. [2], the amplitude of individual pulses in RPTs is about two order of magnitude smaller than the return stroke (RS) pulses. Moreover, the observation made by Rakov et al. [2] shows that the RPTs occur both in cloud flashes and during cloud activity between return strokes.

Chaotic pulse trains (CPTs) were first observed by Weidman [3]. Since the CPTs that Weidman observed occurred during the leader stage of the subsequent return strokes, he coined the name “chaotic subsequent return stroke” to represent subsequent return strokes preceded by chaotic pulse bursts. Subsequent studies demonstrated that CPTs can also occur in the electric fields of cloud flashes without any return strokes [4,5,6]. Gomes et al. [6] observed the occurrence of CPTs in ground flashes either just before the subsequent return strokes or without any association with subsequent return strokes. According to Gomes et al. [6], the width of the individual pulses of CPTs is within the range of a few microseconds with minimum ranges into the sub microsecond scale. The inter-pulse duration lies within the range of 2–20 µs, and duration of the CPT is 400–500 µs.

The discharge mechanism by which a CPT is generated in lightning flashes is currently unknown. In this paper, we make an attempt to understand the origin of CPTs in lightning flashes. First, we collect electric field records containing the typical signatures of RPTs and CPTs generated from lightning discharges. Then we use the measured RPTs in a numerical analysis to show that a typical CPT could be a result of sum of more than one RPTs. This finding then suggests that the possible origin of CPTs could be several RPTs taking place simultaneously in cloud during a lightning discharge.

2. Methodology

2.1. Measurement

Measurements of electric field signatures generated by negative cloud-to-ground (CG) flashes pertinent to Swedish thunderstorms were recorded from May to August 2014 during summer at Uppsala (59.837° N, 17.646° E). The site is located 70 km inland of the Baltic Sea and 38 m above sea level. The distances to the negative CG flashes from the measurement site were estimated by using the Swedish lightning location network (LLN). The flashes being analyzed here ranged from 10 to 100 km from the measuring station. The timing for each event was provided by a global positioning system (GPS). The wideband electric field was recorded by a calibrated flat plate antenna located 1.5 m above ground. The antenna system consisting of a parallel flat plate antenna together with an electronic buffer circuits for fast electric field measurements is identical to the ones used previously in the studies reported in references [7,8,9]. Moreover, a narrowband electric field (3 MHz) was also recorded. The high frequency (HF) radiation at 3 MHz was detected by a tuned antenna system whose electric field sensing flat plate was located on the roof of a 3-m-high van located in the vicinity of the wideband antenna. The field enhancement caused by placing the antenna over the roof of the van was obtained by connecting the antenna located on the roof of the van to a wideband system and comparing the amplitudes of wideband signals measured simultaneously by two antennas (i.e., one located aboveground and the other located on the roof of the van).

A 60-cm-long coaxial cable (RG58) was used to connect the antenna to the electronic buffer circuit for the fast electric fields. The zero-to-peak rise time of the output was shorter than 30 ns when the step inputs pulse was applied to the fast electric field antenna system. The decay time constant for the fast electric field antenna, which is determined by the RC constant of the electronics, was 15 ms. The decay time constant of the fast electric field antenna was found to be sufficient for the faithful reproduction of microsecond scale field changes. The tuned circuit at 3 MHz is a combination of passive elements where the inductance (47 µH) is connected in series with the antenna (58 pF) and 50 Ω termination forming a simple RCL circuit. The bandwidth of the tuned circuits at 3 MHz is 264 kHz.

Signals from both wideband and narrowband systems were fed into a digital transient recorder (Yokogawa SL 1000 equipped with DAQ modules 720210) through proper termination (50 Ω resistor). The wideband signal was fed to this 12-bit digitizer by 10-m-long coaxial cables (RG-58), whereas 3 MHz signal was fed by a 3-m-long cable. The sampling time was set to 250 ms at a sampling interval of 10 ns. A pre-trigger time of 30% of the total time window (250 ms) was used in these measurements. The trigger setting of the oscilloscope was set such that the signals of both polarities could trigger the system.

2.2. Data

In this measurement campaign a total of 98 lightning flashes were found where both wideband and 3 MHz signals were successfully measured simultaneously. In 64 of these flashes either a RPT(s), or a CPT(s) or both were found. We did not analyse all these records for this study but only considered those cases (18 lightning flashes) where both RPTs and CPTs were present without having any time separation or any other events (for example downward dart or dart-stepped leader pulses) between them. We have observed that RPTs and CPTs had appeared differently in different flashes so we classified them into four categories. Category 1 (RPT–CPT): a CPT that started with an RPT (16 trains in eight lightning flashes); Category 2 (CPT–RPT): a CPT that ended with an RPT (10 trains in six lightning flashes); Category 3 (RPT–CPT–RPT): a CPT that both started and ended with an RPT (6 trains in two lightning flashes); and Category 4 (CPT–RPT–CPT): a CPT that had an RPT in the middle of it (4 trains in two lightning flashes). Figure 1a–d shows examples of these four categories respectively. Three megahertz signals for respective wideband records are also shown in these figures. Figure 1a shows a pulse train that started with a positive regular pulse train which lasted for about 170 µs, which was then followed by a chaotic pulse train that lasted for about 75 µs. In the example shown in Figure 1b, the chaotic train started at about 200 µs before continuing up as a regular pulse train, which was about 190 µs long. Figure 1c shows a pulse burst where the chaotic pulses appear in the middle of the regular pulse trains. Observe that the polarity of the pulses in the RPTs is opposite to each other. Also in certain instances, regular pulses of the same polarity appeared in the middle of the pulse train as shown in Figure 1d. The convention to define the polarity of pulses is an atmospheric electricity sign convention. According to this convention, a negative charge in a cloud produces a negative field at ground level, and a negative return stroke produces a positive field change.

It should be noted that all RPTs and CPTs irrespective of the categories above were observed in between return strokes. There were a total of 36 trains. The average time separation from the end of the previous RS to the beginning of the trains (all categories) was about 24 ± 14 ms, whereas the time separation from the end of the trains (all categories) to the beginning of the following RS was about 4 ± 2 ms. Figure 2a shows an example of a flash where a sequence of RPT-CPT (category 1) was found between first and second RS. Sixteen trains found for category 1 were distributed in between RS in the way such that eight trains appeared between first and second RS, six trains appeared between second and third RS, and two trains appeared between third and fourth RS. Note that for category 1, 16 trains mean 16 distinct RPTs and 16 distinct CPTs. In category 2, 10 trains were found, where six trains appeared between first and second RS, three trains appeared between second and third RS, and one train appeared between third and fourth RS. Note that for category 2, 10 trains mean 10 distinct RPTs and 10 distinct CPTs. In category 3, six trains were found, where two trains appeared between first and second RS, three trains appeared between second and third RS, and one train appeared between third and fourth RS. Note that for category 3, six trains mean six distinct CPTs but 12 distinct RPTs. Because, for each CPT there were one RPT before and one after. Finally, in category 4, four trains were found, where two trains appeared between first and second RS, one train appeared between second and third RS, and one train appeared between third and fourth RS. Note that for category 4, four trains mean 4 distinct RPTs but 8 distinct CPTs as there were two CPTs for each RPT. Thus, the total sum of all distinct RPTs and CPTs were 42 and 40 respectively.

3. Results and Discussion

3.1. Characteristics of the Regular Pulse Train (RPT)

Pulses in the RPT occur at quite regular time intervals. Each pulse in the RPT begins with a fast large-amplitude portion, followed by a small and slowly varying overshoot. However, in some pulses, the opposite overshoot is not that pronounced. If we consider any pulse with an opposite overshoot to be bipolar, then almost all the pulses we observed in the present study can be categorized as bipolar. However, in a study conducted by Kolmasova and Santolik [10], each individual pulse is considered to be unipolar if the immediately following overshoot of the opposite polarity does not exceed one-half of the peak amplitude of the original’s pulse. If we use this criterion, then most of the individual pulses in the RPT should be categorized as unipolar. In Figure 2b an RPT is shown which is an expansion from Figure 2a. Note that the polarity of the pulses is negative here.

As described in Section 2.2, there were a total of 42 distinct RPTs and the total number of individual pulses in these regular pulse trains was 800. On average, each RPT had about 22 pulses. The individual pulse duration (PD) has an arithmetic mean and standard deviation of about 2 ± 1.0 µs and one typical individual pulse is shown in Figure 2c, where the PD also is marked. A sequence of pulses normally persists for 23–98 µs with an arithmetic mean and standard deviation of inter-pulse duration (IPD) of about 5 ± 1.3 µs. The IPD is the time duration between the maximum amplitude of two consecutive pulses in the train as shown in Figure 2d.

As mentioned in Section 2.2, all RPTs took place in between return strokes and the distribution of these trains was following: 20 distinct RPTs were located between the first and the second RS, 16 distinct RPTs were located between the second and the third RS, and 6 distinct RPTs were located between the third and the fourth RS. The amplitude of the pulses in the RPTs were calculated as a fraction of the following return stroke amplitude. The average electric field amplitude of pulses in the RPT was about one-fifth of the electric field peak of the return stroke, and this ratio varied from 0.1 to 0.4.

All values presented here regarding the parameters of PD and IPD agreed with the values found by Krider et al. [1] but the values for the total duration of the pulse trains in our case were much lower than that of Krider et al. This can be explained by the fact that the values of the inter-stroke interval for temperate regions (Uppsala) are shorter than that for subtropical regions such as Florida and Arizona [7].

3.2. Characteristics of the Chaotic Pulse Train (CPT)

There were a total of 1120 individual pulses in those 40 distinct CPTs found in this study. Each distinct CPT had about 28 pulses on average. Figure 3a shows an example of CPT which is an expansion of the CPT in Figure 2a. Because of their chaotic behavior, especially with regard to their amplitudes, pinpointing the exact beginning and end of each pulse in the CPT with good precision is difficult. The total duration (TD) of the CPT is estimated using the criterion adopted by Gomes et al. [6]. According to this criterion, TD is the time duration between the regions of pulse activity at the start and end of the pulse train where the pulse amplitude is equal to 10% of the maximum amplitude in the CPT. In several cases where the noise level was high, we had to increase this limiting value to 20%. In our study, the observed duration, TD, of the CPTs varied from 20 to 120 µs. We estimated the TD, PD and IPD manually with an estimated uncertainty of about ±0.5 µs. Pulse duration (PD) is the width of an individual pulse when the amplitude at the start and end of the individual pulse is equal to 10% of the maximum amplitude in the CPT. The width of each pulse or its duration (PD) varied within the range of 0.5 to 13 µs with an arithmetic mean and standard deviation of about 4 and 3 µs, respectively. The inter-pulse duration (IPD) is the time duration between the maximum amplitude of two consecutive pulses in the train. The IPD varied within the range from 2 to 13 µs with an arithmetic mean and standard deviation of about 8 and 5 µs, respectively. In Figure 3b which is an expansion of Figure 3a, PD and IPD are shown.

As mentioned in Section 2.2, all CPTs took place in between return strokes and the distribution of these trains was following: 20 distinct CPTs were located between the first and the second RS, 14 distinct CPTs were located between the second and the third RS, and 6 distinct CPTs were located between the third and the fourth RS. As for the amplitudes, sometimes pulses with the largest amplitudes occur immediately after the initiation of the chaotic pulse train, and in some cases, the occurrence of the largest peak happens either in the middle and/or at the end of the chaotic pulse train. The arithmetic mean and standard deviation of the ratio of the maximum amplitude of the pulses to the following return stroke peak were 0.4 ± 0.3.

A comparison of the pulse characteristics found in our study to Gomes et al. [6] shows a good agreement but the total train duration is not comparable due to the fact that Gomes et al. analyzed and presented data from three different geographical regions together, namely from Sweden, Denmark and Sri Lanka.

3.3. HF Radiation (3 MHz)

We recorded the HF radiation at 3 MHz simultaneously with the CPT and the RPT. The HF radiation associated with CPTs was previously reported by Gomes et al. [6] and Mäkela et al. [11], but as far as we know there were no reports on measured HF radiation associated with RPTs. Figure 1a–d, Figure 2e and Figure 3c show several examples of HF radiation associated with the CPT and the RPT. Our general observation was that 3 MHz signal corresponding to an RPT had also a regular pattern. Moreover, we found that as a regular pulse had an initial peak followed by an opposite overshoot, the 3 MHz signal density behaved consistently with less oscillation compared to a chaotic pulse train. As a chaotic pulse had an erratic shape, the 3 MHz signal density showed also an erratic nature. On the other hand, 3 MHz signal corresponding to a CPT showed more irregular pattern where the amplitudes could either be increased or decreased significantly compared to the amplitudes of a 3 MHz signal in response to an RPT. This information was important because it was easier to find the transition from one type of pulse train to another type of pulse train in the 3 MHz signal and this was used to confirm the transition between the trains in wideband signal. This can be seen in Figure 1a–d where the transition is marked with dotted line.

3.4. Numerical Analysis: Construction of a CPT through the Numerical Superposition of RPTs

The similarity in the width of individual pulses in both regular pulse trains and chaotic pulse trains and the occurrence of regular pulse trains at the start, in the middle, or at the end of chaotic pulse trains suggested to us the hypothesis that these chaotic pulses are probably created by the superposition of several regular pulse bursts at random times. This is a reasonable physical scenario because during lightning flashes, there could be instances where several dart or dart-stepped leaders, like discharge processes, are simultaneously active in the cloud. Each dart-stepped like leader produces an RPT, and the sum of the signals from all the dart-stepped-like leaders will appear as a CPT. In this section, we will demonstrate this by superimposing RPTs numerically. We will also show that the CPTs constructed in this manner also have Fourier spectrums similar to the ones estimated from the measured CPTs.

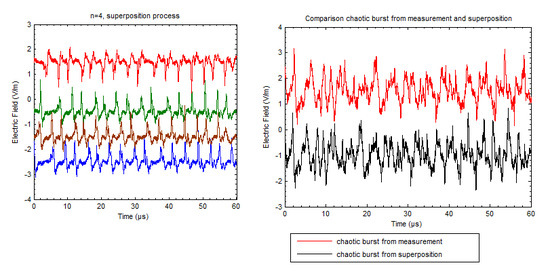
To realize this, out of 42 distinct RPTs we chose one RPT randomly to start with. After selecting a 15- to 60-µs-long section, we took another section from the same RPT with the same length but this time the start of the new section was shifted in time to either direction with 2–5 µs compared to the previous section. In the case of category 3 (RPT–CPT–RPT) where two distinct RPTs were present, sometimes we chose sections of RPTs from both RPTs and sometimes from only one distinct RPT. Then we made a superposition of these two sections. The simulated signal was then compared to the measured CPT belonging to the corresponding train. The comparison was based on their erratic behaviour and the temporal characteristics. This procedure was repeated as a trial and error method. Number of sections that were superimposed, duration of the train section and the position in time of the chosen sections were changed until the best combination was found that corresponded the measured CPT satisfactorily. In Figure 4a,b the results of our numerical simulation are shown, indicating the best combinations with three (Figure 4a) and four RPTs (Figure 4b) and with the 60-µs-long section.

In the numerical superposition, we tried superimposing either the RPT of the same polarity or RPTs with mixed polarities (i.e., adding both positive and negative RPTs to create CPTs). Both procedures gave rise to chaotic-type pulse bursts. The reason we tried constructing a CPT with mixed polarity was because our records showed that we occasionally observed the polarity of pulses in the RPTs changing their polarities. In other words, the RPT may start with pulses of one polarity and then change pulses toward the end of the polarity. This showed us that in some situations it is possible for an RPT of one polarity to interact with an RPT of the opposite polarity in creation of CPTs.

Interestingly, the resulting pulse trains have all the characteristics similar to those observed in chaotic pulse trains. The similarity of the simulated CPT to the ones measured strongly suggests that these pulse trains are created by a series of dart-stepped leader like discharges propagating simultaneously in the cloud.

Since, according to our suggestion, the chaotic pulse burst is a superposition of several regular pulse bursts, the HF associated with the chaotic pulse burst can be treated as the sum of the HF radiation associated with regular pulse bursts. When different HF radiation pulses overlap, depending on their phases, sometimes the resulting amplitude is smaller than that of the RPT, and sometimes it is larger. This means that the peak amplitudes of the HF radiation pulses from chaotic pulse trains will be smaller than that of an RPT in some cases, and it could be larger in other cases.

Figure 2e and Figure 3c show several examples of HF radiation associated with the RPT and the CPT. Figure 1b shows the HF radiation associated with a CPT that ended as an RPT. Observe that the amplitude of the HF radiation associated with the regular pulse train is less than the amplitude of the HF radiation associated with the chaotic pulse train. However, Figure 1c,d shows that the amplitude of the HF radiation associated with an RPT is larger than the amplitude of the HF radiation associated with a CPT. In these cases, one can see the occurrence where the CPT is in the middle of an RPT and the RPT is in the middle of a CPT. The different trends of the amplitude of HF for a CPT and an RPT in some cases are due to destructive and constructive interference. The sum of amplitudes of several RPTs can be less than the amplitudes of all original RPTs, or less than the amplitudes of only a few of the original RPTs but higher than the amplitudes of the remaining original RPTs, or the sum of amplitudes of several RPTs can even be zero because of destructive interference. Meanwhile, when the sum of amplitudes of several RPTs lines up, there is constructive interference. This one can immediately be seen from the recorded data shown in Figure 1a–d.

We also analysed the Fourier spectrum of the measured CPT and compared the results with the ones obtained from the simulated CPT. The results of the comparison are shown in Figure 5a,b. Note that the Fourier spectrums of constructed and measured CPTs are almost identical, and they have a peak around 200 kHz. This similarity of the Fourier spectrums also suggests the common origin of RPTs and CPTs.

4. Conclusions

In this paper, electromagnetic field radiation bursts known as CPTs and RPTs generated by lightning flashes were analysed. In addition to providing the statistical data for the features of chaotic pulse trains (CPTs) and regular pulse trains (RPTs), we hypothesized, based on the features of measured RPTs and CPTs, that the CPTs are possibly formed by a superposition of RPTs. The validity of the hypothesis was demonstrated by constructing CPTs by superimposing several RPTs. The remarkable similarity of the Fourier spectrums for constructed and measured CPTs further demonstrates the validity of the hypothesis. Based on this, we suggest that CPTs are nothing but a random superposition of a series of RPTs created by several dart-stepped leader or K-changes type discharges propagating simultaneously inside the clouds.