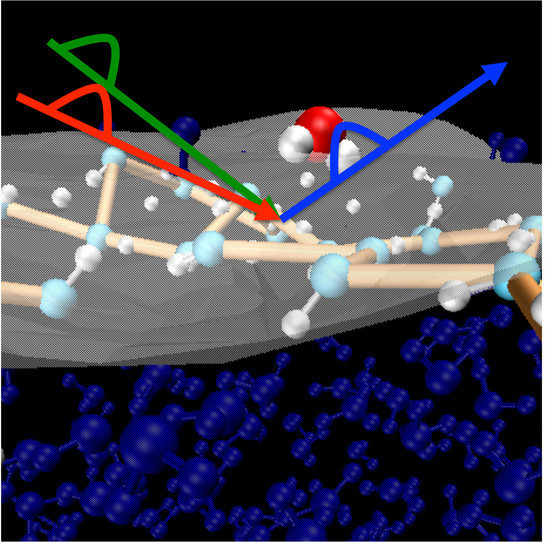
Spectroscopic BIL-SFG Invariance Hides the Chaotropic Effect of Protons at the Air-Water Interface
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
3.1. Solvation of the Hydronium Cation in the BIL
3.2. BIL & DL Water Layers and SFG Spectroscopy: DL-SFG Dominates the Spectral Changes at the Acidic Air/Water Interface
3.3. Beyond BIL-SFG Invariance: The Chaotropic Effect of Hydronium at the Air-Water Interface
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Laskin, A.; Gaspar, D.J.; Wang, W.; Hunt, S.W.; Cowin, J.P.; Colson, S.D.; Finlayson-Pitts, B.J. Reactions at Interfaces as a Source of Sulfate Formation in Sea Salt Particles. Science 2003, 301, 340–344. [Google Scholar] [CrossRef] [PubMed]
- Dawson, M.; Varner, M.E.; Perraud, V.; Ezell, M.J.; Gerber, R.B.; Finlayson-Pitts, B.J. Simplified Mechanism for New Particle Formation from Methane Sulfonic Acid, Amines, and Water via Experiments and Ab Initio Calculations. Proc. Nat. Acad. Sci. USA 2012, 109, 18719–18724. [Google Scholar] [CrossRef] [PubMed]
- Knipping, E.M.; Lakin, M.J.; Foster, K.L.; Jungwirth, P.; Tobias, D.J.; Gerber, R.B.; Dabdub, D.; Finlayson-Pitts, B.J. Experiments and Simulations of Ion-Enhanced Interfacial Chemistry on Aqueous NaCl Aerosols. Science 2000, 288, 301–306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Katrib, Y.; Deiber, G.; Schweitzer, F.; Mirabel, P.; George, C. Chemical Transformation of Bromine Chloride at the Air/Water Interface. J. Aerosol Sci. 2001, 32, 893–911. [Google Scholar] [CrossRef]
- Clifford, D.; Donaldson, D.J. Direct Experimental Evidence for a Heterogeneous Reaction of Ozone with Bromide at the Air- Aqueous Interface. J. Phys. Chem. A 2007, 111, 9809–9814. [Google Scholar] [CrossRef] [PubMed]
- Laskin, A.; Wang, H.; Robertson, W.H.; Cowin, J.P.; Ezell, M.J.; Finlayson-Pitts, B.J. A New Approach to Determining Gas-Particle Reaction Probabilities and Application to the Heterogeneous Reaction of Deliquesced Sodium Chloride Particles with Gas-Phase Hydroxyl Radicals. J. Phys. Chem. A 2006, 110, 10619–10627. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.D.; Roberts, J.T.; Anderson, L.D.; Grassian, V.H. The 367 nm PhotoChemistry of OClO Thin Films and OClO Adsorbed on Ice. J. Phys. Chem. 1996, 100, 19551–19558. [Google Scholar] [CrossRef]
- Shen, Y.R.; Ostroverkhov, V. Sum-Frequency Vibrational Spectroscopy on Water Interfaces: Polar Orientation of Water Molecules at Interfaces. Chem. Rev. 2006, 106, 1140–1154. [Google Scholar] [CrossRef] [PubMed]
- Allen, H.C.; Casillas-Ituarte, N.N.; Sierra-Hernandez, M.R.; Chen, X.; Tang, C.Y. Shedding light on water structure at air-aqueous interfaces: Ions, lipids, and hydration. Phys. Chem. Chem. Phys. 2009, 11, 5538–5549. [Google Scholar] [CrossRef] [PubMed]
- Jubb, A.; Hua, W.; Allen, H. Environmental Chemistry at Vapor/Water Interfaces: Insights from Vibrational Sum Frequency Generation Spectroscopy. Annu. Rev. Phys. Chem. 2012, 63, 107–130. [Google Scholar] [CrossRef] [PubMed]
- Jungwirth, P.; Winter, B. Ions at Aqueous Interfaces: From Water Surface to Hydrated Proteins. Annu. Rev. Phys. Chem. 2008, 59, 343–366. [Google Scholar] [CrossRef] [PubMed]
- Nihonyanagi, S.; Kusaka, R.; Inoue, K.; Adhikari, A.; Yamaguchi, S.; Tahara, T. Accurate Determination of Complex χ(2) Spectrum of the Air/Water Interface. J. Chem. Phys. 2015, 143, 124707. [Google Scholar] [PubMed]
- Zhang, Z.; Piatkowski, L.; Bakker, H.; Bonn, M. Ultrafast Vibrational Energy Transfer at the Water/Air Interface Revealed by Two-Dimensional Surface Vibrational Spectroscopy. Nat. Chem. 2011, 3, 888–893. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Liang, R.; Xu, X.; Zhu, H.; Shen, Y.R.; Tian, C. Phase Reference in Phase-Sensitive Sum-Frequency Vibrational Spectroscopy. J. Chem. Phys. 2016, 144, 244711. [Google Scholar] [CrossRef] [PubMed]
- Ishiyama, T.; Imamura, T.; Morita, A. Theoretical Studies of Structures and Vibrational Sum Frequency Generation Spectra at Aqueous Interfaces. Chem. Rev. 2014, 114, 8447–8470. [Google Scholar] [CrossRef] [PubMed]
- Kessler, J.; Elgabarty, H.; Spura, T.; Karhan, K.; Partovi-Azar, P.; Hassanali, A.A.; Kuhne, T.D. Structure and Dynamics of the Instantaneous Water/Vapor Interface Revisited by Path-Integral and Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. B 2015, 119, 10079–10086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Willard, A.; Chandler, D. Instantaneous Liquid Interfaces. J. Phys. Chem. B 2010, 114, 1954–1958. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, Q.; Freysz, E.; Shen, Y.R. Vibrational Spectroscopy of Water at the Vapor/Water Interface. Phys. Rev. Lett. 1993, 70, 2313–2316. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Shen, Y.R. Recent progress on sum-frequency spectroscopy. Surf. Sci. Rep. 2014, 69, 105. [Google Scholar] [CrossRef]
- Wen, Y.C.; Zha, S.; Liu, X.; Yang, S.; Guo, P.; Shi, G.; Fang, H.; Shen, Y.R.; Tian, C. Unveiling Microscopic Structures of Charged Water Interfaces by Surface-Specific Vibrational Spectroscopy. Phys. Rev. Lett. 2016, 116, 016101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pezzotti, S.; Galimberti, D.R.; Shen, Y.R.; Gaigeot, M.P. Structural definition of the BIL and DL: A new universal methodology to rationalize non-linear chi(2)(omega) SFG signals at charged interfaces, including chi(3)(omega) contributions. Phys. Chem. Chem. Phys. 2018, 20, 5190–5199. [Google Scholar] [CrossRef] [PubMed]
- Pezzotti, S.; Galimberti, D.R.; Gaigeot, M.P. 2D H-Bond Network as the Topmost Skin to the Air-Water Interface. J. Phys. Chem. Lett. 2017, 8, 3133–3141. [Google Scholar] [CrossRef] [PubMed]
- Ostroverkhov, V.; Waychunas, G.A.; Shen, Y.R. New Information on Water Interfacial Structure Revealed by Phase-Sensitive Surface Spectroscopy. Phys. Rev. Lett. 2005, 94, 046102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tian, C.; Waychunas, G.A.; Shen, Y.R. J. Am. Chem. Soc. 2008, 130, 7686. [CrossRef] [PubMed]
- Yamaguchi, S. Development of Single-channel Heterodyne-detected Sum Frequency Generation Spectroscopy and its Application to the Water/Vapor Interface. J. Chem. Phys. 2015, 143, 034202. [Google Scholar] [CrossRef] [PubMed]
- Pezzotti, S.; Serva, A.; Gaigeot, M.P. 2D-HB-Network at the air-water interface: A structural and dynamical characterization by means of ab-initio and classical molecular dynamics simulations. J. Chem. Phys. 2018, 148, 174701–174710. [Google Scholar] [CrossRef] [PubMed]
- Serva, A.; Pezzotti, S.; Bougueroua, S.; Galimberti, D.R.; Gaigeot, M.P. Combining ab-initio and classical molecular dynamics simulations to unravel the structure of the 2D-HB-network at the air-water interface. J. Mol. Struct. 2018, 1165, 71–78. [Google Scholar] [CrossRef]
- Gonella, G.; Lutgebaucks, C.; de Beer, A.G.F.; Roke, S. Second Harmonic and Sum-Frequency Generation from Aqueous Interfaces Is Modulated by Interference. J. Phys. Chem. C. 2016, 120, 9165–9173. [Google Scholar] [CrossRef]
- Ohno, P.E.; Saslow, S.A.; Wang, H.F.; Geiger, F.M.; Eisenthal, K.B. Phase-referenced nonlinear Spectroscopy of the alpha-quartz/water Interface. Nat. Comm. 2016, 7, 13587–13591. [Google Scholar] [CrossRef] [PubMed]
- Joutsuka, T.; Hirano, T.; Sprik, M.; Morita, A. Effects of third-order susceptibility in sum frequency generation spectra: A molecular dynamics study in liquid water. Phys. Chem. Chem. Phys. 2018, 20, 3040–3053. [Google Scholar] [CrossRef] [PubMed]
- Pezzotti, S.; Galimberti, D.R.; Shen, Y.R.; Gaigeot, M.P. What the Diffuse Layer (DL) Reveals in Non-Linear SFG Spectroscopy. Minerals 2018, 8, 305. [Google Scholar] [CrossRef]
- Tian, C.; Ji, N.; Waychunas, G.A.; Shen, Y.R. Interfacial Structures of Acidic and Basic Aqueous Solutions. J. Am. Chem. Soc. 2008, 130, 13033–13039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hua, W.; Verreault, D.; Allen, H.C. Relative Order of Sulfuric Acid, Bisulfate, Hydronium, and Cations at the Air013Water Interface. J. Am. Chem. Soc. 2015, 137, 13920–13926. [Google Scholar] [CrossRef] [PubMed]
- Tarbuck, T.L.; Ota, S.T.; Richmond, G.L. Spectroscopic Studies of Solvated Hydrogen and Hydroxide Ions at Aqueous Surfaces. J. Am. Chem. Soc. 2006, 128, 14519–14527. [Google Scholar] [CrossRef] [PubMed]
- Petersen, P.B.; Saykally, R.J. Evidence for an Enhanced Hydronium Concentration at the Liquid Water Surface. J. Phys. Chem. B 2005, 109, 7976–7980. [Google Scholar] [CrossRef] [PubMed]
- Petersen, P.B.; Saykally, R.J. Is the liquid water surface basic or acidic? Macroscopic vs. molecular-scale investigations. Chem. Phys. Lett. 2008, 458, 255–261. [Google Scholar] [CrossRef]
- Buch, V.; Milet, A.; Vácha, R.; Jungwirth, P.; Devlin, J.P. Water surface is acidic. Proc. Nat. Acad. Sci. USA 2007, 104, 7342–7347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giberti, F.; Hassanali, A.A. The excess proton at the air-water interface: The role of instantaneous liquid interfaces. J. Chem. Phys. 2017, 146, 244703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baer, M.D.; Kuo, I.F.W.; Tobias, D.J.; Mundy, C.J. Toward a Unified Picture of the Water Self-Ions at the Air-Water Interface: A Density Functional Theory Perspective. J. Phys. Chem. B 2014, 118, 8364–8372. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Chen, H.; Wang, F.; Paesani, F.; Voth, G.A. An Improved Multistate Empirical Valence Bond Model for Aqueous Proton Solvation and Transport. J. Phys. Chem. B 2008, 112, 467–482. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, H.; Maruyama, K.; Karino, Y.; Morita, A.; Nakano, M.; Jungwirth, P.; Matubayasi, N. Energetic Origin of Proton Affinity to the Air/Water Interface. J. Phys. Chem. B 2011, 115, 4745–4751. [Google Scholar] [CrossRef] [PubMed]
- Tse, Y.L.S.; Chen, C.; Lindberg, G.E.; Kumar, R.; Voth, G.A. Propensity of Hydrated Excess Protons and Hydroxide Anions for the Air-Water Interface. J. Am. Chem. Soc. 2015, 137, 12610–12616. [Google Scholar] [CrossRef] [PubMed]
- Wick, C.D. Hydronium Behavior at the Air-Water Interface with a Polarizable Multistate Empirical Valence Bond Model. J. Phys. Chem. C 2012, 116, 4026–4038. [Google Scholar] [CrossRef]
- Kumar, R.; Knight, C.; Voth, G.A. Exploring the behaviour of the hydrated excess proton at hydrophobic interfaces. Faraday Discuss. 2013, 167, 263–278. [Google Scholar] [CrossRef] [PubMed]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. CP2K: Atomistic Simulations of Condensed Matter Systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef] [Green Version]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach. Comp. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- Grimme, S. Accurate Description of Van der Waals Complexes by Density Functional Theory Including Empirical Corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- White, J.A.; Schwegler, E.; Galli, G.; Gygi, F. The Solvation of Na+ in Water: First-Principles Simulations. J. Chem. Phys. 2000, 113, 4668–4673. [Google Scholar] [CrossRef]
- Morita, A.; Hynes, J.T. A Theoretical Analysis of the SFG Spectrum of the Water Surface. II-Time Dependent Approach. J. Phys. Chem. B 2002, 106, 673–685. [Google Scholar] [CrossRef]
- Morita, A.; Ishiyama, T. Recent Progress in Theoretical Analysis of Vibrational Sum Frequency Generation Spectroscopy. Phys. Chem. Chem. Phys. 2008, 10, 5801–5816. [Google Scholar] [CrossRef] [PubMed]
- Khatib, R.; Backus, E.H.G.; Bonn, M.; Perez-Haro, M.J.; Gaigeot, M.P.; Sulpizi, M. Water Orientation and Hydrogen-Bond Structure at the Fluorite/Water Interface. Sci. Rep. 2016, 6, 24287. [Google Scholar] [CrossRef] [PubMed]
- Corcelli, S.A.; Skinner, J.L. Infrared and Raman Line Shapes of Dilute HOD in Liquid H2O and D2O from 10 to 90 C. J. Phys. Chem. A 2005, 109, 6154–6165. [Google Scholar] [CrossRef] [PubMed]
- Urashima, S.H.; Myalitsin, A.; Nihonyanagi, S.; Tahara, T. The Topmost Water Structure at a Charged Silica/Aqueous Interface Revealed by Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 4109–4114. [Google Scholar] [CrossRef] [PubMed]
- Weissenborn, P.K.; Pugh, R.J. Surface Tension of Aqueous Solutions of Electrolytes: Relationship with Ion Hydration, Oxygen Solubility, and Bubble Coalescence. J. Colloid Interface Sci. 1996, 184, 550–563. [Google Scholar] [CrossRef] [PubMed]
- Hassanali, A.; Giberti, F.; Cuny, J.; Kühne, T.D.; Parrinello, M. Proton transfer through the water gossamer. Proc. Natl. Acad. Sci. USA 2013, 110, 13723–13728. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Knyazev, D.G.; Vereshaga, Y.A.; Ippoliti, E.; Nguyen, T.; Carloni, P.; Pohl, P. Water at hydrophobic interfaces delays proton surface-to-bulk transfer and provides a pathway for lateral proton diffusion. Proc. Natl. Acad. Sci. USA 2012, 109, 9744–9749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Li, Z.; Si, W.; Lin, K.; Ma, J.; Li, K.; Sun, L.; Sha, J.; Chen, Y. Identification of Single Nucleotides by a Tiny Charged Solid-State Nanopore. J. Phys. Chem. B 2018, 122, 7929–7935. [Google Scholar] [CrossRef] [PubMed]






| n of HBs/Molecule | |||||
|---|---|---|---|---|---|
| System | L0 | L1 | L2 | L3 | intra-2DN |
| AW-neat | 1.9 | 2.9 | 3.4 | 3.4 | 1.7 |
| AW + HO | 1.9 | 2.9 | 3.4 | 3.4 | 1.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pezzotti, S.; Gaigeot, M.-P. Spectroscopic BIL-SFG Invariance Hides the Chaotropic Effect of Protons at the Air-Water Interface. Atmosphere 2018, 9, 396. https://doi.org/10.3390/atmos9100396
Pezzotti S, Gaigeot M-P. Spectroscopic BIL-SFG Invariance Hides the Chaotropic Effect of Protons at the Air-Water Interface. Atmosphere. 2018; 9(10):396. https://doi.org/10.3390/atmos9100396
Chicago/Turabian StylePezzotti, Simone, and Marie-Pierre Gaigeot. 2018. "Spectroscopic BIL-SFG Invariance Hides the Chaotropic Effect of Protons at the Air-Water Interface" Atmosphere 9, no. 10: 396. https://doi.org/10.3390/atmos9100396
APA StylePezzotti, S., & Gaigeot, M. -P. (2018). Spectroscopic BIL-SFG Invariance Hides the Chaotropic Effect of Protons at the Air-Water Interface. Atmosphere, 9(10), 396. https://doi.org/10.3390/atmos9100396