Observation of the Dynamics and Horizontal Dispersion in a Shallow Intermittently Closed and Open Lake and Lagoon (ICOLL)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Environmental and Inlet Conditions during the Field Experiments
2.3. Instrumentation
2.4. Data Analysis
2.5. Measurement Uncertainty from Fixed Stationary Drifter
3. Results and Discussion
3.1. Basic Flow and Physiochemical Observations
3.2. Horizontal Surface Dispersion Coefficient
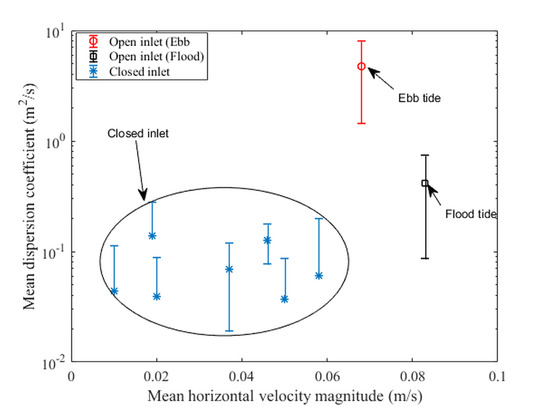
Effect of Inlet on the Dispersion Coefficient
3.3. Differential Kinematic Properties
3.4. Horizontal Dispersion Mechanisms within the Channel
3.4.1. Open State (E1)
3.4.2. Closed State (E2)
3.5. Implications for Current Lake Management Strategies
4. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Effect of Position Error on Observed Parameters
| Parameter (Unit) | Component | Test 1 Duration = 4 h | Test 2 Duration = 5.8 h | Test 3 Duration = 8.3 h |
|---|---|---|---|---|
| Centroid (m) | E | −0.16–0.16 | −0.18–0.18 | −0.16–0.16 |
| N | −0.28–0.28 | −0.16–0.16 | −0.19–0.19 | |
| Velocity × 10−2 (m s−1) | E | −0.028–0.032 | −0.015–0.029 | −0.000–0.002 |
| N | −0.001–0.004 | −0.001–0.009 | 0.000–0.003 | |
| Dispersion coefficient (m2 s−1) | Effective | −0.001–0.0013 | −0.002–0.0001 | 0.000–0.003 |
| Differential Kinematic properties × 10−5 (s−1) | Vorticity | −2.1–1.1 | −2.9–2.4 | −2.0–2.7 |
| Shearing | −0.8–2.2 | −2.4–2.9 | −2.2–2.4 | |
| Stretching | −1.6–1.1 | −1.5–3.8 | −5.7–6.8 | |
| Divergence | −1.6–1.3 | −1.7–3.8 | −2.6–2.1 |
References
- Gale, E.; Pattiaratchi, C.; Ranasinghe, R. Processes driving circulation, exchange and flushing within intermittently closing and opening lakes and lagoons. Mar. Freshw. Res. 2007, 58, 709–719. [Google Scholar] [CrossRef]
- Pollard, D. Opening regimes and salinity characteristics of intermittently opening and permanently open coastal lagoons on the south coast of New South Wales. Wetl. Aust. J. 1994, 13, 16–35. [Google Scholar]
- Roy, P.; Williams, R.; Jones, A.; Yassini, I.; Gibbs, P.; Coates, B.; West, R.; Scanes, P.; Hudson, J.; Nichol, S. Structure and function of south-east Australian estuaries. Estuar. Coast. Shelf Sci. 2001, 53, 351–384. [Google Scholar] [CrossRef]
- Milbrandt, E.C.; Bartleson, R.D.; Coen, L.D.; Rybak, O.; Thompson, M.A.; DeAngelo, J.A.; Stevens, P.W. Local and regional effects of reopening a tidal inlet on estuarine water quality, seagrass habitat, and fish assemblages. Cont. Shelf Res. 2012, 41, 1–16. [Google Scholar] [CrossRef]
- Schallenberg, M.; Larned, S.T.; Hayward, S.; Arbuckle, C. Contrasting effects of managed opening regimes on water quality in two intermittently closed and open coastal lakes. Estuar. Coast. Shelf Sci. 2010, 86, 587–597. [Google Scholar] [CrossRef]
- Gale, E.; Pattiaratchi, C.; Ranasinghe, R. Vertical mixing processes in intermittently closed and open lakes and lagoons, and the dissolved oxygen response. Estuar. Coast. Shelf Sci. 2006, 69, 205–216. [Google Scholar] [CrossRef]
- Wiles, P.J.; van Duren, L.A.; Häse, C.; Larsen, J.; Simpson, J.H. Stratification and mixing in the Limfjorden in relation to mussel culture. J. Mar. Syst. 2006, 60, 129–143. [Google Scholar] [CrossRef]
- Geyer, W.R.; Signell, R.P. A reassessment of the role of tidal dispersion in estuaries and bays. Estuaries 1992, 15, 97–108. [Google Scholar] [CrossRef]
- Uncles, R.J.; Torres, R. Estimating dispersion and flushing time-scales in a coastal zone: Application to the Plymouth area. Ocean Coast. Manag. 2013, 72, 3–12. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, E.J.; Koh, R.C.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: New York, NY, USA, 1979; ISBN 0122581504. [Google Scholar]
- Riddle, A.; Lewis, R. Dispersion experiments in UK coastal waters. Estuar. Coast. Shelf Sci. 2000, 51, 243–254. [Google Scholar] [CrossRef]
- Shaha, D.; Cho, Y.-K.; Kwak, M.-T.; Kundu, S.; Jung, K. Spatial variation of the longitudinal dispersion coefficient in an estuary. Hydrol. Earth Syst. Sci. 2011, 15, 3679–3688. [Google Scholar] [CrossRef] [Green Version]
- Suara, K.A.; Wang, C.; Feng, Y.; Brown, R.J.; Chanson, H.; Borgas, M. High resolution GNSS-tracked drifter for studying surface dispersion in shallow water. J. Atmos. Ocean. Technol. 2015, 32, 579–590. [Google Scholar] [CrossRef]
- George, R.; Largier, J.L. Description and performance of finescale drifters for coastal and estuarine studies. J. Atmos. Ocean. Technol. 1996, 13, 1322–1326. [Google Scholar] [CrossRef]
- Tseng, R.S. On the dispersion and diffusion near estuaries and around islands. Estuar. Coast. Shelf Sci. 2002, 54, 89–100. [Google Scholar] [CrossRef]
- Suara, K.A.; Brown, R.J.; Borgas, M. Eddy diffusivity: A single dispersion analysis of high resolution drifters in a tidal shallow estuary. Environ. Fluid Mech. 2016, 16, 923–943. [Google Scholar] [CrossRef]
- Stocker, R.; Imberger, J. Horizontal transport and dispersion in the surface layer of a medium-sized lake. Limnol. Oceanogr. 2003, 48, 971–982. [Google Scholar] [CrossRef] [Green Version]
- Bowden, K.F. Horizontal mixing in the sea due to a shearing current. J. Fluid Mech. 1965, 21, 83–95. [Google Scholar] [CrossRef]
- Kettle, D.S.; Edwards, P.B.; Barnes, A. Factors affecting numbers of Culicoides in truck traps in coastal Queensland. Med. Vet. Entomol. 1998, 12, 367–377. [Google Scholar] [CrossRef] [PubMed]
- Lühken, R.; Steinke, S.; Wittmann, A.; Kiel, E. Impact of flooding on the immature stages of dung-breeding culicoides in northern europe. Vet. Parasitol. 2014, 205, 289–294. [Google Scholar] [CrossRef] [PubMed]
- Tomlinson, R.; Williams, P.; Richards, R.; Weigand, A.; Schlacher, T.; Butterworth, V.; Gaffet, N. Lake Currimundi Dynamics Study Final Report Volume 1 and 2; Griffith Centre for Coastal Management, Griffith University: Southport, Australia, 2010. Available online: https://www.sunshinecoast.qld.gov.au/Environment/Rivers-and-Coast/Lake-Currimundi-Dynamics-Study (accessed on 1 May 2017).
- Okubo, A. Oceanic diffusion diagrams. Deep Sea Res. Oceanogr. Abstr. 1971, 18, 789–802. [Google Scholar] [CrossRef]
- Suara, K.; Ketterer, T.; Fairweather, H.; McCallum, A.; Vanaki, S.M.; Allan, C.; Brown, R. Cluster Dispersion of Low-Cost GPS-Tracked Drifters in a Shallow Water. Proceedings of 10th Australasian Heat and Mass Transfer Conference, Brisbane, Australia, 14–15 July 2016; Australasian Fluid and Thermal Engineering Society: Brisbane, Australia, 2016. [Google Scholar]
- ABM. Australian Government Bureau of Meteorology. Daily Global Solar Exposure. 2015. Available online: http://www.bom.gov.au/jsp/ncc/cdio/weatherData/av?p_nccObsCode=193&p_display_type=dailyDataFile&p_startYear=2015&p_c=-336226903&p_stn_num=040998 (accessed on 11 April 2018).
- SCC. More Than 90% Pesky Midges Wiped Out. Available online: https://www.sunshinecoast.qld.gov.au/Council/News-Centre/Currimundi-Lake-reopening-18-October-2016 (accessed on 12 May 2017).
- Suara, K.A. Development and Use of GPS-Based Technology to Study Dispersion in Shallow Water. Ph.D. Thesis, Science and Engineering Faculty, Queensland University of Technology, Brisbane, Australia, 2017. [Google Scholar]
- Elder, J.W. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Madhani, J.T.; Dawes, L.A.; Brown, R.J. A perspective on littering attitudes in Australia. Environ. Eng. J. Soc. Sustain. Environ. Eng. 2009, 9, 13–20. [Google Scholar]
- Suara, K.; Wang, H.; Chanson, H.; Gibbes, B.; Brown, R. Response of GPS-tracked drifters to wind and water currents in a tidal estuary. IEEE J. Ocean. Eng. 2018, in press. [Google Scholar]
- List, E.J.; Gartrel, G.; Winant, C.D. Diffusion and dispersion in coastal waters. J. Hydraul. Eng. 1990, 116, 1158–1179. [Google Scholar] [CrossRef]
- Okubo, A.; Ebbesmeyer, C.C. Determination of vorticity, divergence, and deformation rates from analysis of drogue observations. Deep Sea Res. Oceanogr. Abstr. 1976, 23, 349–352. [Google Scholar] [CrossRef]
- Molinari, R.; Kirwan, A.D., Jr. Calculations of differential kinematic properties from Lagrangian observations in the western Caribbean sea. J. Phys. Oceanogr. 1975, 5, 483–491. [Google Scholar] [CrossRef]
- Truesdell, C. The Kinematics of Vorticity; Indiana University Press: Bloomington, IN, USA, 1954. [Google Scholar]
- Okubo, A. Some speculation on oceanic diffusion diagrams. Rapp. P.-V. Reun. Cons. Int. Explor. Mer. 1974, 167, 77–85. [Google Scholar]
- Suara, K.; Chanson, H.; Borgas, M.; Brown, R.J. Relative dispersion of clustered drifters in a small micro-tidal estuary. Estuar. Coast. Shelf Sci. 2017, 194, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Johnson, D.; Stocker, R.; Head, R.; Imberger, J.; Pattiaratchi, C. A compact, low-cost GPS drifter for use in the oceanic nearshore zone, lakes, and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 1880–1884. [Google Scholar] [CrossRef]
- Chanson, H.; Brown, R.J.; Trevethan, M. Turbulence measurements in a small subtropical estuary under king tide conditions. Environ. Fluid Mech. 2012, 12, 265–289. [Google Scholar] [CrossRef] [Green Version]
- Manning, J.P.; Churchill, J.H. Estimates of dispersion from clustered-drifter deployments on the southern flank of Georges Bank. Deep Sea Res. Part II 2006, 53, 2501–2519. [Google Scholar] [CrossRef] [Green Version]
- Pinton, J.-F.; Sawford, B.L. A Lagrangian view of turbulent dispersion and mixing. In Ten Chapters in Turbulence; Davidson, P.A., Kaneda, Y., Sreenivasan, K.R., Eds.; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Spydell, M.S.; Feddersen, F.; Olabarrieta, M.; Chen, J.; Guza, R.T.; Raubenheimer, B.; Elgar, S. Observed and modeled drifters at a tidal inlet. J. Geophys. Res. Oceans 2015, 120, 4825–4844. [Google Scholar] [CrossRef] [Green Version]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind characteristics and resources. In Wind Energy Explained; John Wiley & Sons, Ltd.: West Sussex, UK, 2009; pp. 23–89. [Google Scholar]
- Geyer, W.R.; Trowbridge, J.H.; Bowen, M.M. The dynamics of a partially mixed estuary. J. Phys. Oceanogr. 2000, 30, 2035–2048. [Google Scholar] [CrossRef]
- Okubo, A. Effect of shoreline irregularities on streamwise dispersion in estuaries and other embayments. Neth. J. Sea Res. 1973, 6, 213–224. [Google Scholar] [CrossRef]
- Delpeche-Ellmann, N.; Torsvik, T.; Soomere, T. A comparison of the motions of surface drifters with offshore wind properties in the Gulf of Finland, the Baltic sea. Estuar. Coast. Shelf Sci. 2016, 172, 154–164. [Google Scholar] [CrossRef]
- Carpenter, S.; Mellor, P.S.; Torr, S.J. Control techniques for Culicoides biting midges and their application in the UK and northwestern Palaearctic. Med. Vet. Entomol. 2008, 22, 175–187. [Google Scholar] [CrossRef] [PubMed]
- Madhani, J.T. The Hydrodynamic and Capture/Retention Performance of a Gross Pollutant Trap. Ph.D. Thesis, Faculty of Built Environment and Engineering, Queensland University of Technology, Brisbane, Australia, 2010. [Google Scholar]










| Experiment | Date | Inlet Condition | Tide | Tidal Range (m) | Water Depth at X (m) | Daily Mean Solar Exposure (W/m2) | Wind Speed Range (m s−1) | Average Flow Velocity (m s−1) | Instrument Deployed |
|---|---|---|---|---|---|---|---|---|---|
| E1 | 27/4/15–28/4/15 | Open | Flood | 0.60 | 0.4–1.1 | 175 | 0–4.0 | 0.10 | ADV and GPS-drifters, weather station |
| Ebb | 0.5–0.8 | 0.10 | |||||||
| E2 | 09/09/15 | Closed | Non-tidal | 0.00 | 1.1 | 287.5 | 0–7.0 | 0.04 | GPS-drifters, and Sonic anemometer |
| Study | Experiment | Number of Drifters | Duration (s) | VH (m s−1) | Keff (m2 s−1) | ||
|---|---|---|---|---|---|---|---|
| E1 (tidal) | Contraction | Spreading | Effective | ||||
| Ebb | 5–15 | 19,081 | 0.068 | −1.440 | 5.070 | 4.700 | |
| Flood | 5–15 | 10,371 | 0.083 | −0.410 | 0.430 | 0.420 | |
| E2 (Non-tidal) | C1 | 5 | 10,861 | 0.019 | −0.140 | 0.140 | 0.140 |
| C2 | 3–5 | 11,461 | 0.010 | −0.001 | 0.050 | 0.044 | |
| C3 | 4 | 9781 | 0.050 | −0.030 | 0.040 | 0.037 | |
| C4 | 4 | 3721 | 0.020 | −0.033 | 0.048 | 0.039 | |
| C1 | 5 | 6721 | 0.058 | −0.056 | 0.064 | 0.061 | |
| C2 | 3–5 | - | - | - | - | - | |
| C3 | 4 | 6241 | 0.037 | −0.049 | 0.080 | 0.069 | |
| C4 | 4 | 6181 | 0.046 | −0.091 | 0.200 | 0.130 | |
| Study | Experiment | Duration | Differential Kinematic Properties | TK | |||
|---|---|---|---|---|---|---|---|
| E1 (tidal) | (s) | Vorticity × 10−4 s−1 | Divergence × 10−4 s−1 | Shearing × 10−4 s−1 | Stretching × 10−4 s−1 | ||
| Ebb | 19,081 | ** | 8.91 | ** | ** | ||
| Flood | 10,371 | 8.93 | 7.82 | −2.35 | −5.45 | 0.86 | |
| E2 (Non-tidal) | C1 | 10,861 | −17.14 | 5.89 | ** | 16.27 | |
| C2 | 11,461 | 2.53 | 2.82 | ** | 1.77 | ||
| C3 | 9781 | 16.04 | 4.71 | −6.17 | −18.96 | 0.64 | |
| C4 | 3721 | −10.88 | −15.98 | −28.53 | −31.19 | 0.64 | |
| C1 | 6721 | 9.83 | 17.04 | −9.63 | −5.19 | 0.70 | |
| C2 | |||||||
| C3 | 6241 | 1.45 | 5.13 | −4.44 | −2.90 | 0.74 | |
| C4 | 6181 | 61.03 | 11.24 | 5.04 | −52.18 | 0.88 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suara, K.; Mardani, N.; Fairweather, H.; McCallum, A.; Allan, C.; Sidle, R.; Brown, R. Observation of the Dynamics and Horizontal Dispersion in a Shallow Intermittently Closed and Open Lake and Lagoon (ICOLL). Water 2018, 10, 776. https://doi.org/10.3390/w10060776
Suara K, Mardani N, Fairweather H, McCallum A, Allan C, Sidle R, Brown R. Observation of the Dynamics and Horizontal Dispersion in a Shallow Intermittently Closed and Open Lake and Lagoon (ICOLL). Water. 2018; 10(6):776. https://doi.org/10.3390/w10060776
Chicago/Turabian StyleSuara, Kabir, Neda Mardani, Helen Fairweather, Adrian McCallum, Chris Allan, Roy Sidle, and Richard Brown. 2018. "Observation of the Dynamics and Horizontal Dispersion in a Shallow Intermittently Closed and Open Lake and Lagoon (ICOLL)" Water 10, no. 6: 776. https://doi.org/10.3390/w10060776
APA StyleSuara, K., Mardani, N., Fairweather, H., McCallum, A., Allan, C., Sidle, R., & Brown, R. (2018). Observation of the Dynamics and Horizontal Dispersion in a Shallow Intermittently Closed and Open Lake and Lagoon (ICOLL). Water, 10(6), 776. https://doi.org/10.3390/w10060776